
- •Г.В. Соколовська с.Ю. Соколовський тригонометричні рівняння та нерівності
- •§1 Основні означення та формули тригонометрії
- •Графіки тригонометричних функцій
- •Основні тригонометричні формули
- •1. Формули, що зв’язують тригонометричні функції одного аргументу
- •2. Формули додавання
- •3. Формули зведення
- •4. Формули подвійного аргументу
- •5. Формули, що перетворюють суму і різницю тригонометричних функцій на їх добуток
- •6. Формули, що перетворюють добуток тригонометричних функцій на суму і різницю
- •§2 Обернені тригонометричні функції
- •Графіки обернених тригонометричних функцій
- •§3 Тригонометричні рівняння.
- •Введення допоміжного аргументу.
- •§4 Розв’язування найпростіших тригонометричних нерівностей.
- •Вправи для самостійного розв’язування.
§3 Тригонометричні рівняння.
Розв’язування найпростіших тригонометричних рівнянь.
З
властивостей функції
![]() випливає, що рівняння
випливає, що рівняння
![]()
![]()
має
розв’язки лише за умови, що
![]() і множину його розв’язків можна задати
формулою
і множину його розв’язків можна задати
формулою
![]() .
.
![]()
Рівняння
![]()
![]()
також
має розв’язки за умови
![]() ,
їх можна задати формулою
,
їх можна задати формулою
![]() .
.
![]()
Особливий
вигляд мають розв’язки рівнянь
![]() і
і
![]() у тих випадках, коли
у тих випадках, коли
![]() та
та
![]() .
.
![]() при
при
![]() ;
;
![]() при
при
![]() ;
;
![]() при
при
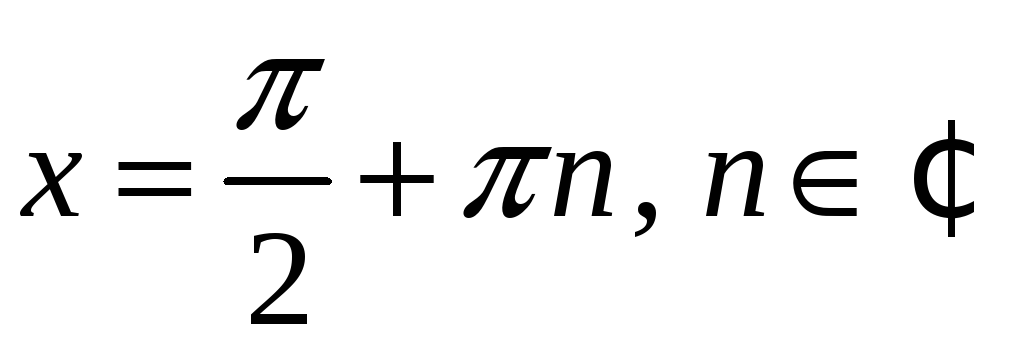 ;
;
![]() при
при
 ;
;
![]() при
при
 ;
;
![]() при
при
![]() .
.
Розв’язки рівняння
![]()
![]()
можна подати у вигляді
![]() ,
,
![]()
а рівняння
![]()
![]()
у вигляді
![]() .
.
![]()
Вправа
12. Розв’язати
рівняння
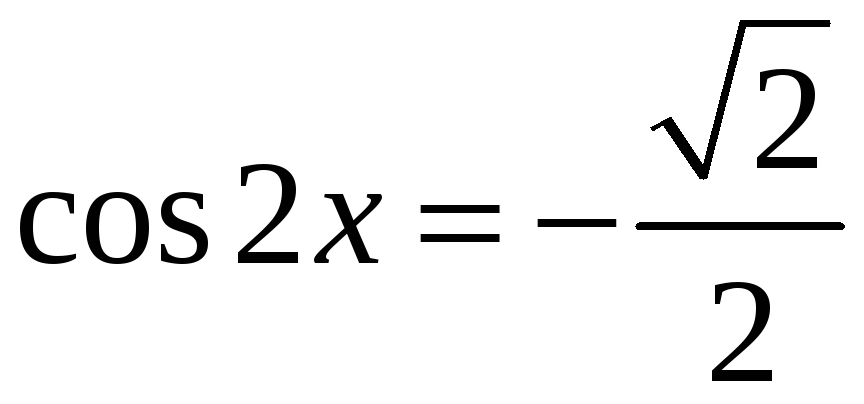 .
.
Розв’язання.
Скористаємось
формулою
![]() .
.

Тоді
 .
.
Вправа
13. Розв’язати
рівняння
 .
.
Розв’язання.
Скористаємось
формулою
![]() .
.
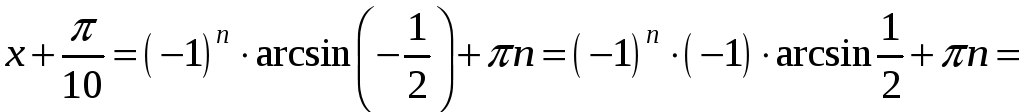
 .
.
Тоді
 .
.
Вправа
14. Розв’язати
рівняння
 .
.
Розв’язання.
Спочатку
запишемо рівняння у вигляді
 .
Скористаємось формулою
.
Скористаємось формулою
![]() .
.
 .
Тоді
.
Тоді
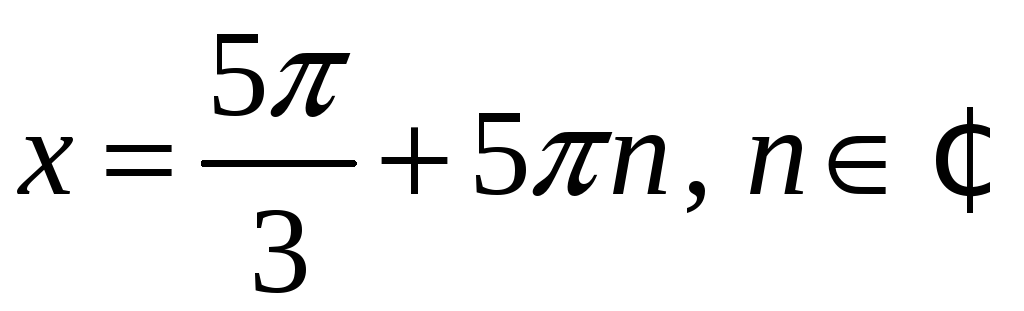 .
.
Вправа
15. Розв’язати
рівняння
 .
.
Розв’язання.
Спочатку
запишемо рівняння у вигляді
 .
Скористаємось формулою
.
Скористаємось формулою
![]() .
.

 .
В остаточній відповіді
.
В остаточній відповіді
![]() замінено
на
замінено
на
![]() ,
оскільки множина їх значень однакова.
,
оскільки множина їх значень однакова.
В деяких тригонометричних рівняннях доречно перейти до нової змінної й розв’язати спочатку алгебраїчне рівняння.
Вправа
16. Розв’язати
рівняння
![]() .
.
Розв’язання.
За основною тригонометричною тотожністю:
![]() або
або
![]() .
.
Нехай
![]() .
Рівняння набуває вигляду
.
Рівняння набуває вигляду
![]() .
Його розв’язки:
.
Його розв’язки:
![]() .
Рівняння
.
Рівняння
![]() не має розв’язків. З рівняння
не має розв’язків. З рівняння
![]() маємо:
маємо:
 .
.
Вправа
17. Розв’язати
рівняння
![]() .
.
Розв’язання.
Область
допустимих значень змінної:
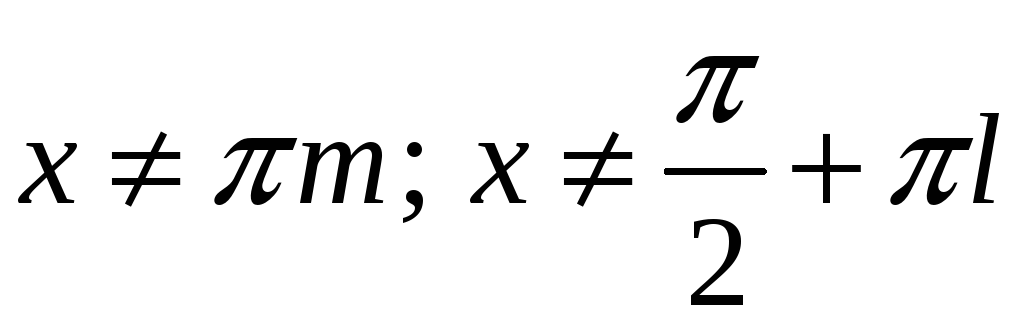 ,
,
![]() .
.
Враховуючи,
що
 ,
і переходячи до нової змінної
,
і переходячи до нової змінної
![]() ,
одержимо:
,
одержимо:
 або
або
 .
Розв’язавши це рівняння одержимо:
.
Розв’язавши це рівняння одержимо:
 або
або
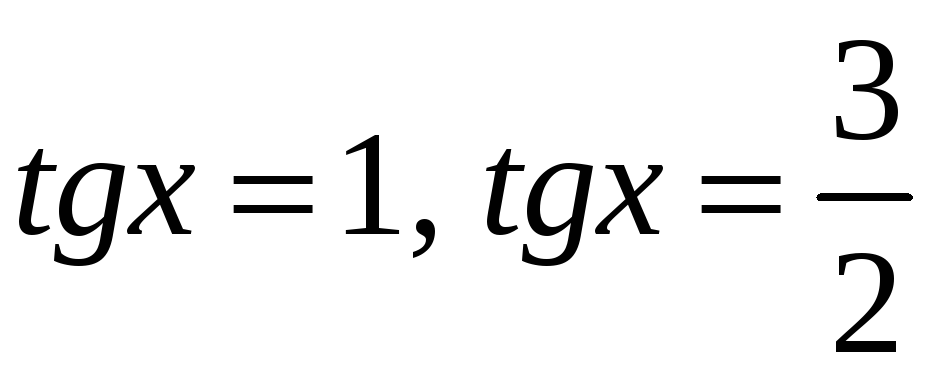 .
Тоді
.
Тоді
 або
або
 .
.
Введення допоміжного аргументу.
Для розв’язання рівняння виду
![]()
![]()
використовують такий алгоритм.
1.
Розділимо обидві частини рівняння на
![]() .
.
2.
Розглянемо таке число
![]() ,
що
,
що
 .
.
Тоді
вихідне рівняння набуває вигляду:
 або
або
 ,
тобто зводиться до вигляду
,
тобто зводиться до вигляду
![]() . Отже, рівняння (37) має розв’язки
. Отже, рівняння (37) має розв’язки
 якщо
якщо
 .
.
Вправа
18. Розв’язати
рівняння
![]() .
.
Розв’язання.
Застосуємо вказану послідовність дій.
-
Розділимо обидві частини рівняння на
 .
Одержимо
.
Одержимо
 .
. -
Враховуючи, що
 ,
маємо:
,
маємо:
 або
або
 .
Звідки отримаємо:
.
Звідки отримаємо:
 або
або
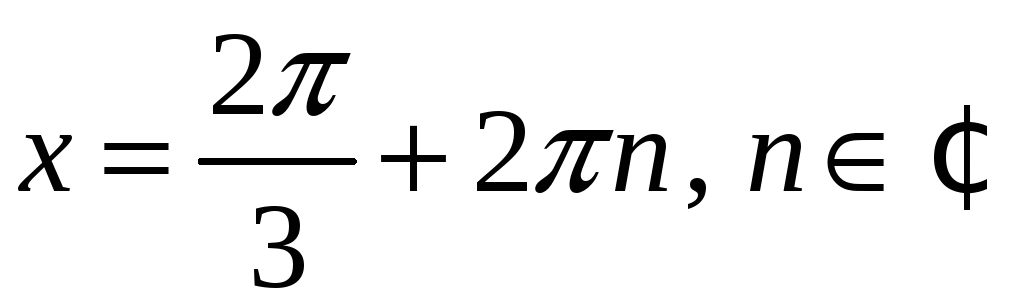 .
.
Однорідні тригонометричні рівняння.
Рівняння
![]() попереднього розділу при
попереднього розділу при
![]() має вигляд
має вигляд
![]()
![]()
і називається однорідним рівнянням першого степеня.
Його
можна розв’язати простіше, розділивши
обидві частини на
![]() .
Зауважимо, що це не приводить до втрати
розв’язків, адже при
.
Зауважимо, що це не приводить до втрати
розв’язків, адже при
 ,
,
![]() ,
ліва частина не дорівнює нулю. Одержимо
,
ліва частина не дорівнює нулю. Одержимо
![]() або
або
 .
Тобто отримаємо рівняння виду
.
Тобто отримаємо рівняння виду
![]() .
.
Вправа
19. Розв’язати
рівняння
![]() .
.
Розв’язання.

Звідки
отримаємо:
 .
.
Рівняння виду
![]()
![]()
називають
однорідним
рівнянням другого степеня. Його
можна розв'язати, розділивши обидві
частини на
![]() .
При цьому ми не втрачаємо розв’язки,
адже при
.
При цьому ми не втрачаємо розв’язки,
адже при
![]() ліва частина не дорівнює
ліва частина не дорівнює
![]() ,
коли
,
коли
![]() .
Одержимо рівняння
.
Одержимо рівняння
![]() ,
яке можна розв’язати за допомогою
введення нової змінної
,
яке можна розв’язати за допомогою
введення нової змінної
![]() .Умовою
розв’язності цього рівняння є виконання
нерівності
.Умовою
розв’язності цього рівняння є виконання
нерівності
![]() .
.
Зауважимо,
що до рівняння виду
![]() можна звести також рівняння
можна звести також рівняння
![]() ,
адже
,
адже
![]() .
.
Вправа
20. Розв’язати
рівняння
![]() .
.
Розв’язання.
Перепишемо рівняння у вигляді:
![]()
![]() .
.
Розділивши
обидві частини на
![]() ,
маємо:
,
маємо:
![]() ,
звідки
,
звідки
![]() або
або
![]() .
.
Отже
 або
або
![]() .
.
Нехай
у рівнянні
![]()
![]() .
Тоді воно має вигляд
.
Тоді воно має вигляд
![]()
і
розпадається на сукупність двох рівнянь
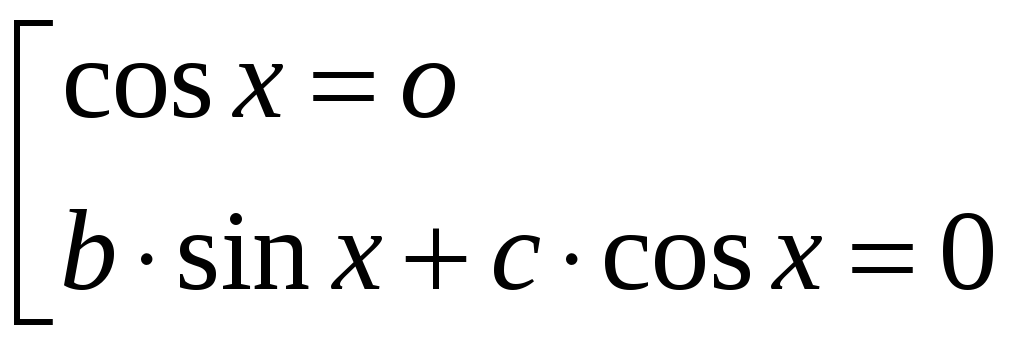 . Перше з цих рівнянь дає
. Перше з цих рівнянь дає
 ,
а обидві частини другого при
,
а обидві частини другого при
![]() можна розділити на
можна розділити на
![]() (адже корені рівняння
(адже корені рівняння
![]() вже враховані). Тоді друге рівняння
набуває вигляду
вже враховані). Тоді друге рівняння
набуває вигляду
 ,
звідки
,
звідки
 .
.
Тригонометричні
рівняння виду
![]() ,
ліва частина яких розкладається на
множники.
,
ліва частина яких розкладається на
множники.
Розклавши ліву частину рівняння на множники, прирівняємо кожен з них до нуля. Таким чином, рівняння розпадається на декілька більш простих рівнянь.
Вправа
21. Розв’язати
рівняння
![]() .
.
Розв’язання.
Знайдемо
спочатку область допустимих значень
(ОДЗ) змінної.
 .
.
Задане
рівняння не рівносильне сукупності
рівнянь
 адже корні першого з них
адже корні першого з них
![]() не можна вважати коренями вихідного
рівняння, оскільки вони не належать
ОДЗ. Корені другого рівняння
не можна вважати коренями вихідного
рівняння, оскільки вони не належать
ОДЗ. Корені другого рівняння
 ,
які належать ОДЗ, і будуть коренями
заданого рівняння.
,
які належать ОДЗ, і будуть коренями
заданого рівняння.
Вправа
22. Розв’язати
рівняння
![]() .
.
Розв’язання.
Перепишемо
рівняння у вигляді
![]() або
або
![]() .
ОДЗ:
.
ОДЗ:
![]() або
або
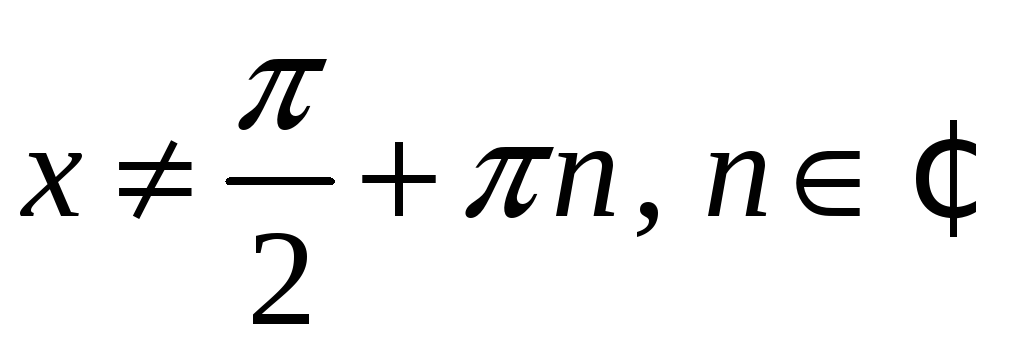 .
.
Розклавши
чисельник на множники, прирівняємо його
до нуля. Одержимо:![]() .
Переходимо до рівносильної йому
сукупності рівнянь
.
Переходимо до рівносильної йому
сукупності рівнянь
 або
або
 .
Друге рівняння не має розв’язків, а
розв’язки першого
.
Друге рівняння не має розв’язків, а
розв’язки першого
![]() ,
належать ОДЗ і є відповіддю.
,
належать ОДЗ і є відповіддю.
Вправа
23. Розв’язати
рівняння
![]() .
.
Розв’язання.
ОДЗ:
![]() .
.
Застосувавши
формулу
![]() одержимо
одержимо
![]() або
або
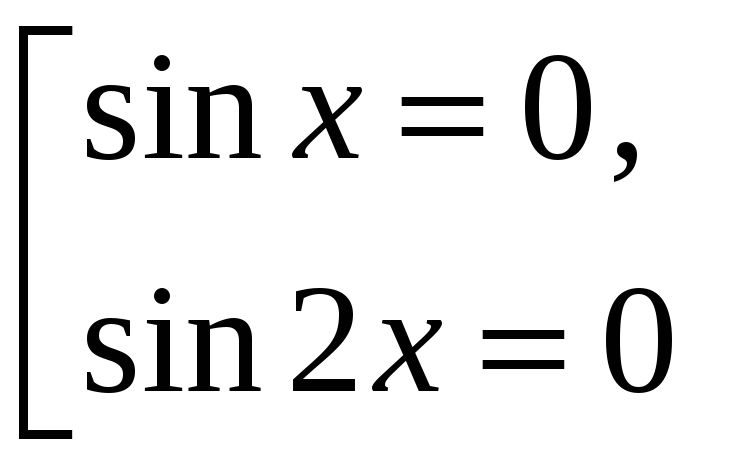 ,
звідки
,
звідки
 .
Зауважимо, що корені першого рівняння
співпадають з тими коренями другого,
які відповідають парним значенням
.
Зауважимо, що корені першого рівняння
співпадають з тими коренями другого,
які відповідають парним значенням
![]() .
Отже вся сукупність розв’язків заданого
рівняння записується у вигляді
.
Отже вся сукупність розв’язків заданого
рівняння записується у вигляді
 .
.
За
допомогою розвинення лівої частини на
множники можна також розв’язати рівняння
![]() і
і
![]() ,
які є частинними випадками рівняння
,
які є частинними випадками рівняння
![]() .
.
Застосувавши
формулу зведення до першого з цих рівнянь
приводимо його до вигляду
 .
Розклавши ліву частину на множники за
формулою
.
Розклавши ліву частину на множники за
формулою
![]() ,
маємо
,
маємо
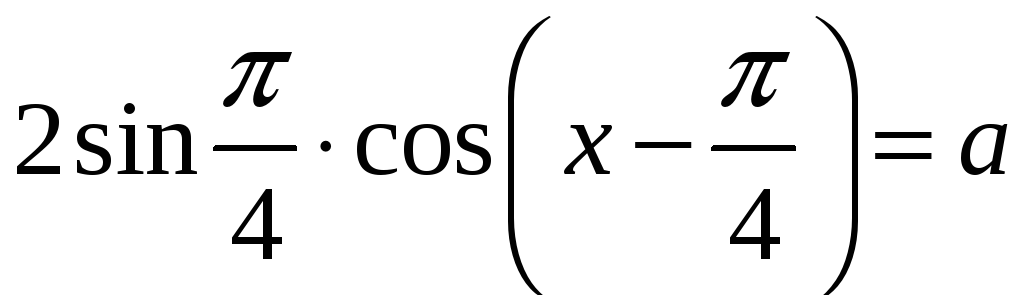 або
або
 .
Умовою його розв’язності є
.
Умовою його розв’язності є
 або
або
![]() .
Тоді
.
Тоді
 .
Друге рівняння розв’язується аналогічно.
.
Друге рівняння розв’язується аналогічно.
Універсальна тригонометрична підстановка.
Вкажемо один загальний метод, що дозволяє розв’язувати рівняння виду
![]() .
.
![]()
Тут
![]() - раціональна функція відносно
- раціональна функція відносно
![]() та
та
![]() .
Для розв’язання рівняння
.
Для розв’язання рівняння
![]() будемо використовувати формули, які
виражають тригонометричні функції
через тангенс половинного кута.
будемо використовувати формули, які
виражають тригонометричні функції
через тангенс половинного кута.
 ,
,
![]()
 ,
,
![]()
де
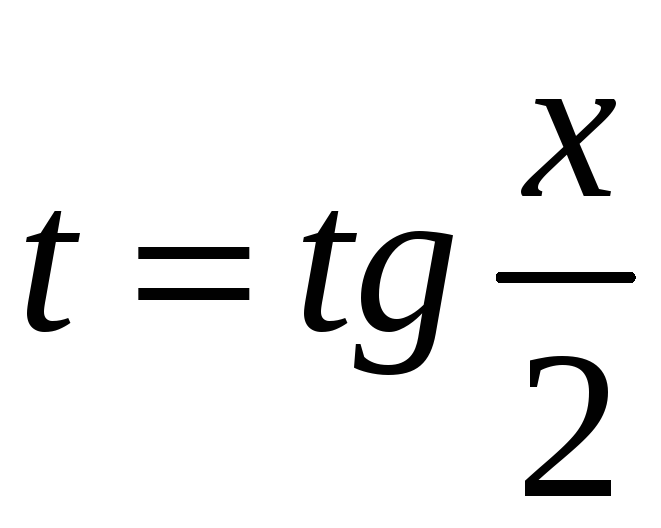 - універсальна тригонометрична
підстановка.
- універсальна тригонометрична
підстановка.
Якщо
підставити в рівняння
![]() вирази
вирази
![]() і
і
![]() ,
одержимо раціональне рівняння відносно
змінної
,
одержимо раціональне рівняння відносно
змінної
![]() .
Розв’язавши його, знайдемо невідому
величину
.
Розв’язавши його, знайдемо невідому
величину
![]() .
Знаючи, що
.
Знаючи, що
 ,
знайдемо
,
знайдемо
![]() .
.
Зауважимо,
що вказана підстановка може привести
до втрати коренів. Тому слід перевірити,
чи не будуть розв’язками рівняння такі
значення
![]() ,
при яких
,
при яких
![]() не існує, тобто
не існує, тобто
 або
або
![]() ,
,
![]() .
.
Вправа
24. Розв’язати
рівняння
![]() .
.
Розв’язання.
Зробивши
універсальну тригонометричну підстановку,
отримаємо
 або
або
 .
Розв’язком якого є
.
Розв’язком якого є
![]() .
Тоді
.
Тоді
![]() ,
звідки
,
звідки
![]() .
.
Перевіримо,
чи будуть числа
![]() ,
розв’язками рівняння.
,
розв’язками рівняння.
![]()
![]() .
Як бачимо, не будуть. Отже, множина всіх
розв’язків записується у вигляді:
.
Як бачимо, не будуть. Отже, множина всіх
розв’язків записується у вигляді:
![]() .
.
Приклади розв’язання різних тригонометричних рівнянь.
Вправа
25. Розв’язати
рівняння
![]() .
.
Розв’язання.
Розділивши
обидві частини рівняння на
![]() одержимо:
одержимо:
 або
або
 .
.
За
формулою
![]() маємо:
маємо:
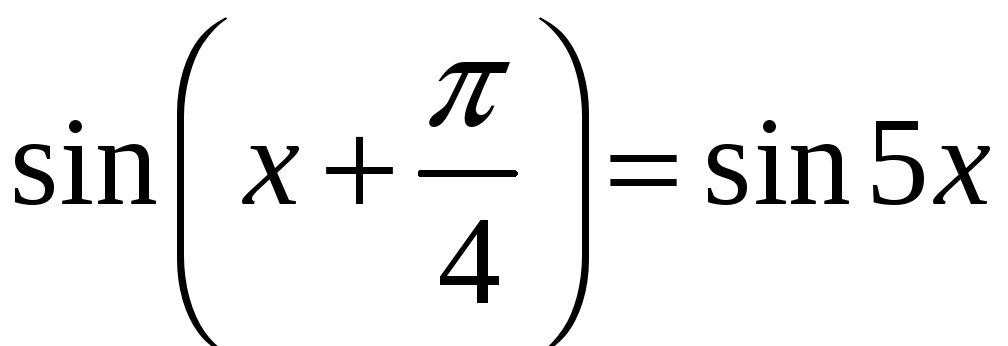 або
або
 .
.
Записавши різницю синусів у вигляді добутку, отримаємо:
 .
.
Тоді
 .
.
Вправа
26. Розв’язати
рівняння
![]() .
.
Розв’язання.
За
допомогою формули
![]() перетворимо рівняння на рівносильне:
перетворимо рівняння на рівносильне:
 або
або
![]() .
Далі маємо:
.
Далі маємо:

 .
Зауважимо,
що корені другого рівняння співпадають
з тими коренями першого, які відповідають
парним значенням
.
Зауважимо,
що корені другого рівняння співпадають
з тими коренями першого, які відповідають
парним значенням
![]() .
Отже сукупність розв’язків заданого
рівняння запишемо у вигляді
.
Отже сукупність розв’язків заданого
рівняння запишемо у вигляді
 .
.
Вправа
27. Розв’язати
рівняння
![]() .
.
Розв’язання.
Застосувавши
формули зниження степеня
![]() перейдемо до рівносильного рівняння:
перейдемо до рівносильного рівняння:
 або
або
![]() .
Тоді
.
Тоді
 .
.
Вправа
28. Розв’язати
рівняння
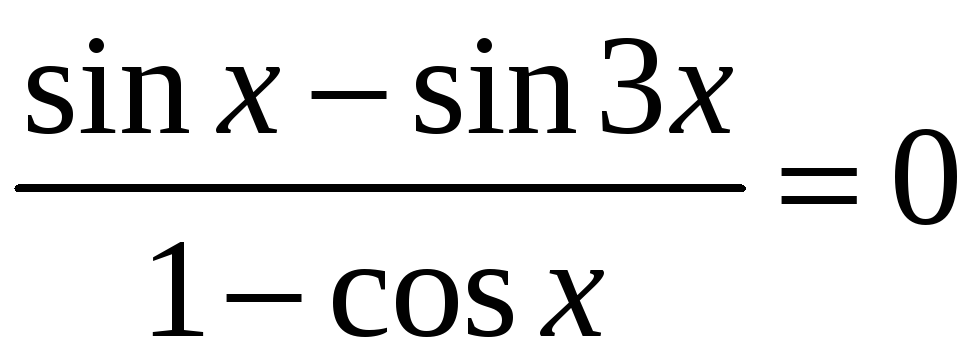 .
.
Розв’язання.
ОДЗ:
![]() .
.
Прирівнявши
чисельник до нуля маємо:
![]() .
Тоді
.
Тоді
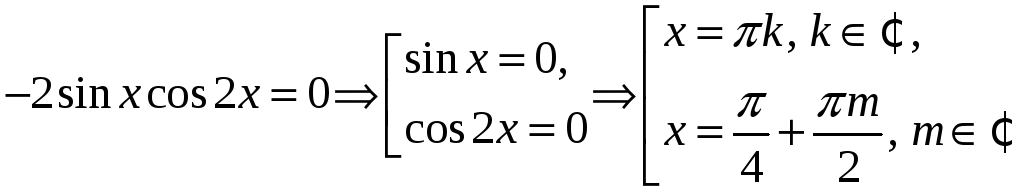 .
Серед отриманих розв’язків рівняння
.
Серед отриманих розв’язків рівняння
![]() є
такі, що не входять до області допустимих
значень заданого рівняння. Їх містить
множина
є
такі, що не входять до області допустимих
значень заданого рівняння. Їх містить
множина
![]() ,
де
,
де
![]() - парне число. Виключивши їх з вказаної
множини, одержимо відповідь:
- парне число. Виключивши їх з вказаної
множини, одержимо відповідь:
 .
.
Вправа
29. Розв’язати
рівняння
![]() .
.
Розв’язання.
Розв’язати
задане рівняння – означає знайти абсцису
точок перетину графіків функцій
![]() та
та
![]() .
Перший з цих графіків - парабола з
вершиною в точці
.
Перший з цих графіків - парабола з
вершиною в точці
![]() .
Вітки параболи спрямовані вгору, отже,
для першої функції виконується нерівність
.
Вітки параболи спрямовані вгору, отже,
для першої функції виконується нерівність
![]() ,
,
![]() .
Для другої функції маємо:
.
Для другої функції маємо:
![]() .
Отже, перетнутись графіки можуть лише
в точці з ординатою
.
Отже, перетнутись графіки можуть лише
в точці з ординатою
![]() .
Оскільки на параболі є лише одна така
точка
.
Оскільки на параболі є лише одна така
точка
![]() ,
то рівняння матиме розв’язок (причому
тільки один) лише в тому випадку, якщо
другий графік проходить через цю точку.
,
то рівняння матиме розв’язок (причому
тільки один) лише в тому випадку, якщо
другий графік проходить через цю точку.
Як
бачимо,
![]() .
Таким чином, рівняння має тільки один
розв’язок:
.
Таким чином, рівняння має тільки один
розв’язок:
![]() .
.
