Графіки тригонометричних функцій

Основні тригонометричні формули

1. Формули, що зв’язують тригонометричні функції одного аргументу

,

,

,

.

2. Формули додавання

,

,

,

,

.

3. Формули зведення

Формули зведення – це формули для перетворення 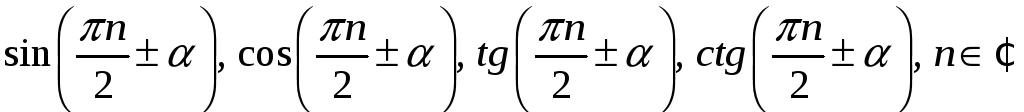, у тригонометричні функції кута .

Наприклад: ,

. Ліву частину кожної з таких формул будемо називати вихідною функцією, а праву частину - зведеною функцією. Для запам’ятовування формул зведення зручно користуватись таким правилом: при переході від тригонометричної функції аргументу до тригонометричної функції аргументу

а) перед зведеною функцією ставимо той знак, який має вихідна функція для початкового аргументу, якщо ;

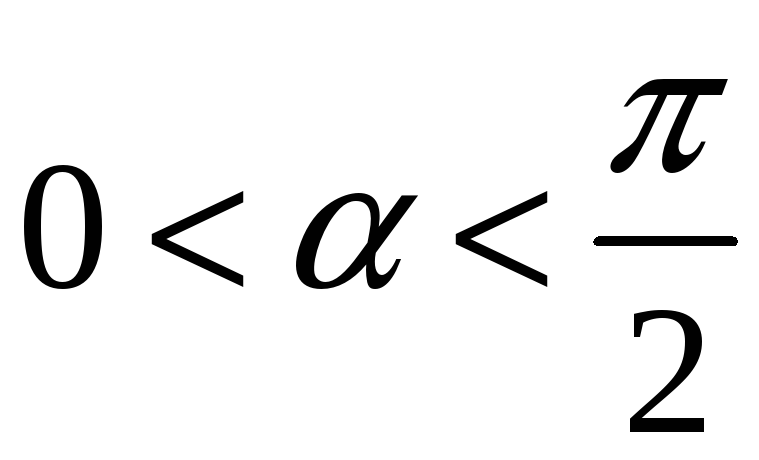б) функція змінюється на "кофункцію", якщо - непарне; функція не змінюється, якщо - парне. (Кофункціями синуса, косинуса, тангенса та котангенса називають відповідно косинус, синус, котангенс і тангенс).

4. Формули подвійного аргументу

,

,

,

,

.

5. Формули, що перетворюють суму і різницю тригонометричних функцій на їх добуток

,

,

,

,

.

6. Формули, що перетворюють добуток тригонометричних функцій на суму і різницю

,

,

.

§2 Обернені тригонометричні функції

Означення. Арксинусом числа називається таке число , синус якого дорівнює .

Наприклад, , адже і .

Означення. Арккосинусом числа називається таке число , косинус якого дорівнює .

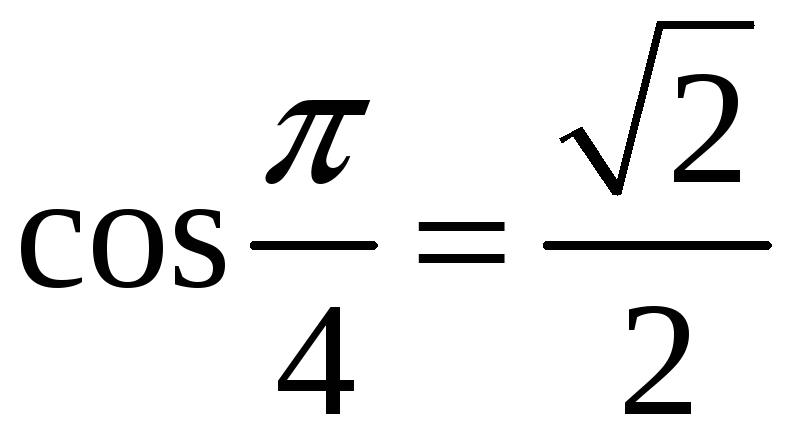Наприклад, , адже і .

Означення. Арктангенсом числа називається таке число , тангенс якого дорівнює .

Означення. Арккотангенсом числа називається таке число , котангенс якого дорівнює .

Користуючись означеннями легко довести, що

Вправа 1.

Обчислити

Розв’язання.

Зауважимо, що

, якщо ;

, якщо ;

, якщо ;

, якщо .

При будь-якому допустимому значенні маємо:

Означення. Функції дійсної змінної, що задаються рівняннями

називаються оберненими тригонометричними функціями арксинус, арккосинус, арктангенс та арккотангенс відповідно.

Графіки обернених тригонометричних функцій

Вправа 2. Обчислити .

Розв’язання.

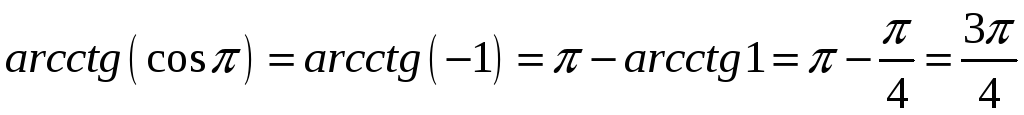
Вправа 3. Обчислити .

Розв’язання.

Враховуючи означення арксинуса, для розв’язання задачі слід відшукати такий кут , що . За формулами зведення маємо: , де . Тоді за формулою (24) маємо:

.

Вправа 4. Обчислити .

Розв’язання.

Так само, як у вправі 3, будемо шукати такий кут , що . Враховуючи періодичність косинуса маємо:

, де .

Тоді за формулою (25) маємо: .

Вправа 5. Обчислити .

Розв’язання.

Для розв’язання задачі слід знайти кут 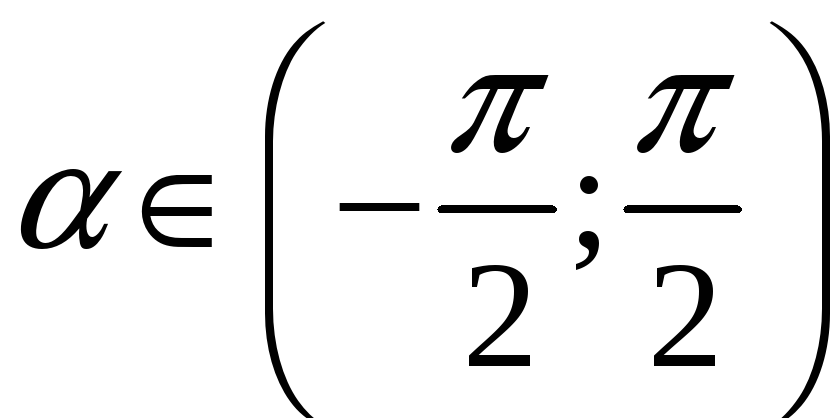такий, що . Скориставшись формулами зведення маємо: 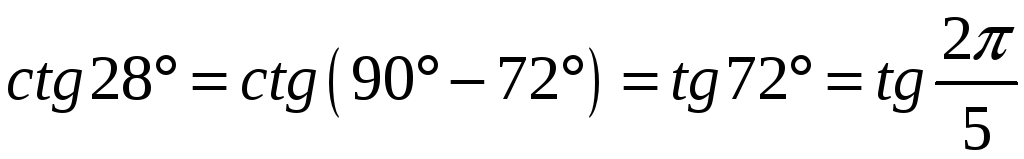. Тоді за формулою (26)

.

Вправа 6. Довести, що .

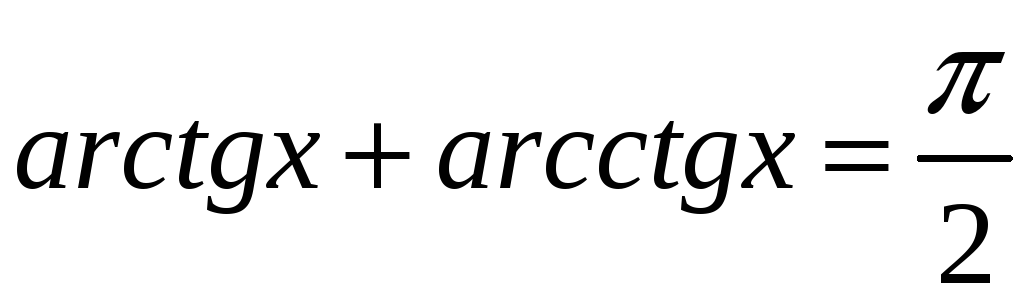Розв’язання.

Доведемо, що . Позначимо і . Оскільки , а , то . На інтервалі функція спадає, тому рівність виконується лише за умови, що . Оскільки , , то . Тоді . Отже .

Вправа 7.

Довести, що , якщо .

Розв’язання.

Позначимо через . За означенням , . Тоді

(оскільки ).

Отже за умови, що .

Вправа 8. Обчислити .

Розв’язання.

.

Вправа 9. Обчислити .

Розв’язання.

.

Вправа 10. Обчислити .

Розв’язання.

Скористаємося формулою , з якої випливає, що . . Отже

.

Вправа 11. Обчислити .

Розв’язання.

.
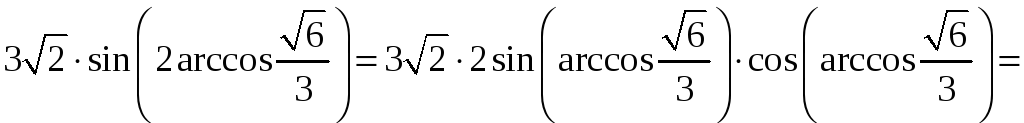