6.3.1.3.Простой алгоритм с упорядоченным списком ребер

Данный метод лежит в основе целого ряда алгоритмов растровой развертки сплошных областей , обьдиненных под общим названием алгоритмов с упорядоченным списком ребер.

Шаги алгоритма:

Определить точки пересечения сканирующих сторон с каждым из ребер многоугольника, игнорируя лишь горизонтальные ребра, и занести в список каждую из точек пересечений (х , у ). Вершины многоугольника , являющиеся локальными минимумами или максимумами , занести в список дважды;

Полученный список отсортировать по строкам и по возрастанию координаты х в каждой строке;

Выделить из отсортированного списка последовательные пары элементов (x_i ,y_i ) (x_(i+1) ,y_(i+1)), где i = 1,3,5, …) и установить для каждой сканирующей строки цвет пикселов, для которых x_i < x < x_(i+1) в цвет многоугольника .

Рассмотрим пример применения этого алгоритма для четырехугольника, отображенном на последнем рисунке.

Список отсортированных пар - точек пересечений ребер многоугольника со сканирующими строками имеет вид:

(4, 1), (4, 1); контур х ?

(3, 2), (4, 2);

(2, 3), (4, 3);

(1, 4), (4, 4);

(1, 5), (4, 5);

(1, 6), (4, 6);

При этом первые две пары мы игнорируем, так как в соответствии с нашими предположениями контуры многоугольника уже существуют. Далее , выделяя пары из этого списка , получаем перечень пикселов, которыу должны быть установлены в заданный цвет:

(3 , 3);

(2, 4), (3, 4);

(2, 5), (3, 5);

(2, 6), (3, 6);

В общем случае в алгоритме с упорядоченным списком ребер генерируется большой список, который нужно отсортировать, поэтому эффективность алгоритма существенно зависит от эффективности сортировки. Следующий алгоритм не использует сортировку при заполнении внутренней области многоугольника.

6.3.1.4.Алгоритм заполнения по ребрам

Единственным шагом этого алгоритма является следующее правило: для каждого ребра многоугольника дополнить все пикселы справа от этого ребра (для всех строк, пересекающих это ребро).

Порядок обработки ребер не важен , однако удобнее это делать последовательно.

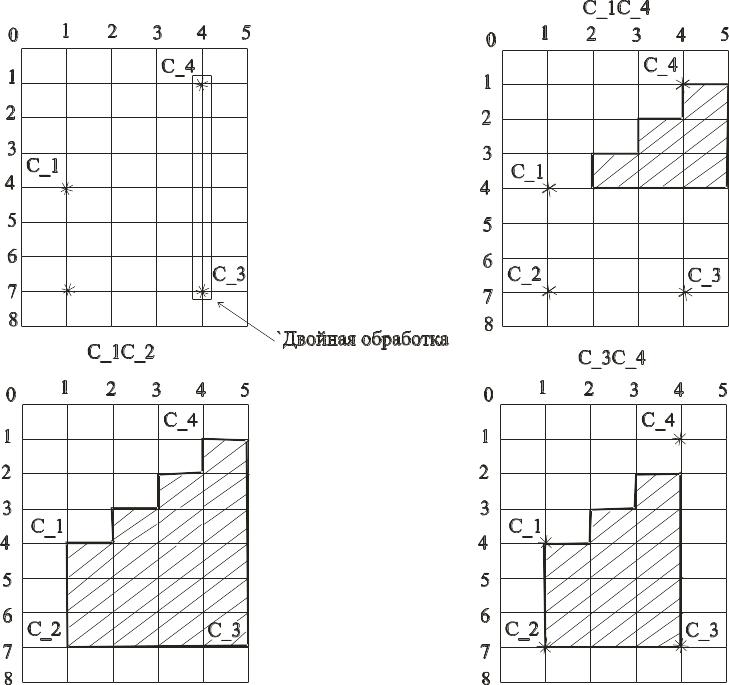
Рис. 6-11

Описанный алгоритм свободен от недостатка предыдущего – необходимости сортировки списка пикселов , но имеет другой.

В рассмотренном примере пикселы с координатами (5, 1), (5, 2), (5, 3), (5, 4), (5, 5), (5, 6), (5, 7) обрабатываются дважды. В более сложных изображениях одни и те же пикселы могут обрабатываться многократно, что снижает эффективность алгоритма в целом. Алгоритм с перегородкой, описанный ниже, позволяет существенно снизить число многократно обрабатываемых пикселов, хотя и не ликвидирует указанный недостаток полностью.

Алгоритм заполнения с перегородкой .

Проведем прегородку через ребро С_3 - С_4 .

Алгоритм заполнения по ребрам с перегородкой заключается в том , что для каждого ребра многоугольника и каждой сканирующей строки происходит дополнение пикселов находящихся между точкой пересечения ребра со скани-рующей строкой и перегородкой .

В нашем примере процесс заполнения предельно прост:

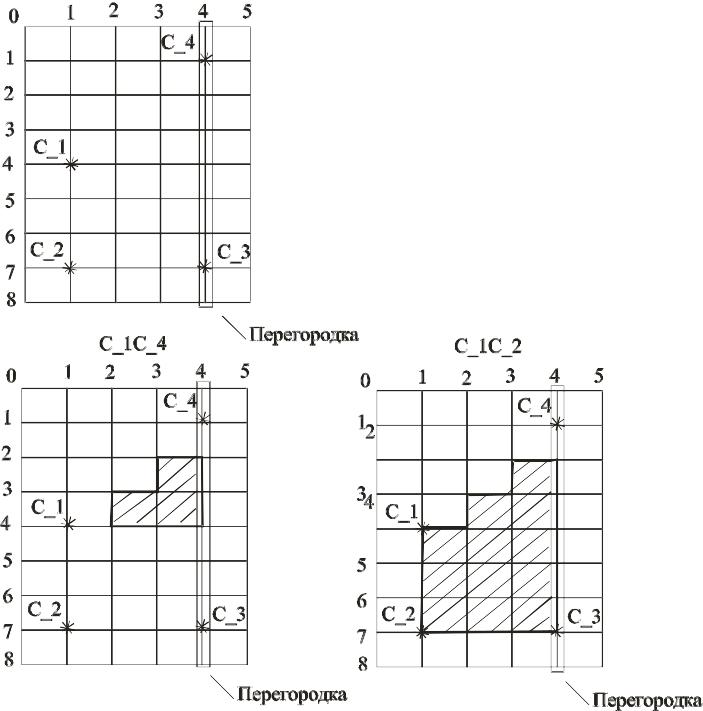
Рис. 6-12

Наиболее часто перегородку проводят через одну из вершин многоугольника. Как следует из нашего примера, проведение перегородки через ребро многоугольника позволяет сократить процесс заполнения на один шаг.