
Підгрупи
Не порожня множина H групи G називається підгрупою, якщо вона є групою відносно визначеної в групі G операції.
Зауважимо, що не
підмножина групи G
є підгрупою. Розглянемо, наприклад
підмножину
![]() групи
групи
![]()
![]() Тут
Тут
![]() .
Отже сума деяких елементів множини А
їй не належать. Якщо тепер множину А
розглядати у відриві від групи, але
з операцією, яка була визначена в групі,
то не для всіх елементів цієї множини
існує сума.
.
Отже сума деяких елементів множини А
їй не належать. Якщо тепер множину А
розглядати у відриві від групи, але
з операцією, яка була визначена в групі,
то не для всіх елементів цієї множини
існує сума.
Критерій підгрупи.
Твердження. Підмножина Н групи G є підгрупою тоді і лише тоді, коли:
а) для довільних
![]() :
:
![]() ;
;
б) для кожного
![]() :
:
![]() .
.
Справді,
умова а) дозволяє ввести на множині
![]() ту ж саму операцію,яка була в групі G
разом з властивістю асоціативності.
ту ж саму операцію,яка була в групі G
разом з властивістю асоціативності.
Умова б) забезпечує існування обернених елементів в . Нарешті, з умов а) і в) випливає, що нейтральний елемент групи належить до
:
![]()
Умови а) і б) можна замінити одною:
![]()
![]() .
.
Пропонуємо, як
вправу, довести, що а), б)
![]() г).
г).
Приклади підгруп:
а) Кожна група G має
так звані тривіальні підгрупи:
![]() і G.
і G.
б) В ланцюгу
![]() кожна попередня група є підгрупою
наступної.
кожна попередня група є підгрупою
наступної.
в) В групі
![]() підгрупою є множина
підгрупою є множина
![]() .
.
г) В групі C(R) підмножина многочленів є підгрупою.
Приклад 1.24. Знайти всі підгрупи .
Розв'язок. Це
дві тривіальні групи:
,![]() .
Підгрупа парних підстановок
.
Підгрупа парних підстановок
![]() з таблицею Келі
з таблицею Келі
|
e a b |
a b |
a b e b e a |
Три підгрупи
другого порядку:
![]()
З однаковими таблицями Келі:
|
e с.. |
e c |
e с c e |
СУМІЖІ КЛАСИ. ТЕОРЕМА ЛАГРАНЖА.
Нехай H
підгрупа групи G.
Задамо відношення
![]() на групі G .
Вважатимемо, що
на групі G .
Вважатимемо, що
![]() ,
тобто два елементи еквівалентні, якщо
добуток
,
тобто два елементи еквівалентні, якщо
добуток
![]() .
Покажемо, що
відношення
еквівалентності.
.
Покажемо, що
відношення
еквівалентності.
а)
![]() бо
бо
![]() (бо
H – підгрупа).
(бо
H – підгрупа).
б) Якщо
![]() ,
то
,
то
![]() .
Дійсно, з того, що
випливає, що і
.
Дійсно, з того, що
випливає, що і
![]() .
.
Однак
![]()
![]() ,
бо
,
бо
![]()
![]() =
=![]()
в) Покажемо, що з
і
![]() випливає
випливає
![]() .
.
Нехай
і
![]() тоді
тоді
![]() ,
бо
підгрупа.
Однак
,
бо
підгрупа.
Однак
![]() =
=
![]() .
.
З а), б), в) випливає,
що
відношення еквівалентності на групі
G. За теоремою 2.5
групі G розбивається
на класи, що не перетинаються:
![]()
Кожен такий клас
![]() складається з тих елементів
складається з тих елементів
![]() ,
що .
,
що .![]() .
Іншими словами, коли
.
Іншими словами, коли
![]() для деякого
,
або
для деякого
,
або
![]() .Отже,
класи еквівалентності – це множини
.Отже,
класи еквівалентності – це множини![]() .
.
Наприклад. а)Нехай
![]() група цілих чисел, кратних числу 3.
Суміжний клас, утворює число 1 є множиною
1+3
група цілих чисел, кратних числу 3.
Суміжний клас, утворює число 1 є множиною
1+3![]() Це всі цілі числа, які при діленні на 3
дають остачу 1. Зрозуміло, що існують
тільки 3 рівні класи групи
Це всі цілі числа, які при діленні на 3
дають остачу 1. Зрозуміло, що існують
тільки 3 рівні класи групи
![]() за підгрупою
за підгрупою
![]()
б) Нехай
![]() ,
,![]() .Суміжний
клас, утворений елементом
.Суміжний
клас, утворений елементом
![]() в
бо
в
бо
![]() ,
а
,
а
![]() .
Елементом
.
Елементом
![]() продовжується клас
продовжується клас
![]() що складається з елементів
що складається з елементів
![]() Ясно,
що більше класів немає, бо
Ясно,
що більше класів немає, бо
![]()
Теорема Лагранжа: Порядок будь-якої підгрупи скінченної групи G є дільником порядку групи.
Доведення:
Оскільки група G є
об’єднанням класів в еквівалентності,
що не перетинаються. А кожен клас містить
однакову кількість елементів![]() ,
де
,
де
![]() порядок
підгрупи
,
то порядок
порядок
підгрупи
,
то порядок
![]() групи G рівний
групи G рівний
![]() ,де
,де
![]() кількість
класів еквівалентності, тобто
=
.Теорему
доведено.
кількість
класів еквівалентності, тобто
=
.Теорему
доведено.
Наслідок. Група простого порядку немає жодних підгруп, крім тривіальних.
Зауваження. Не слід думати, що для будь-якого дільника порядку групи завжди існує підгрупа порядку .
Приклад 1.25.
Нехай
-
підгрупа групи
,
![]() -
фіксований елемент групи
.
Лівим суміжним класом групи
за підгрупою
назвемо
множину елементів виду gh,
де h пробігає всі елементи
підгрупи
;
цю множину позначатимемо через g
.
Аналогічно, множина
-
фіксований елемент групи
.
Лівим суміжним класом групи
за підгрупою
назвемо
множину елементів виду gh,
де h пробігає всі елементи
підгрупи
;
цю множину позначатимемо через g
.
Аналогічно, множина
![]() називається
правим суміжним класом групи
за підгрупою
.
Довести, що таке розбиття групи на класи
співпадає з розбиттям групи на класи
еквівалентності по відношенню, описаному
як
.
називається
правим суміжним класом групи
за підгрупою
.
Довести, що таке розбиття групи на класи
співпадає з розбиттям групи на класи
еквівалентності по відношенню, описаному
як
.
Нехай
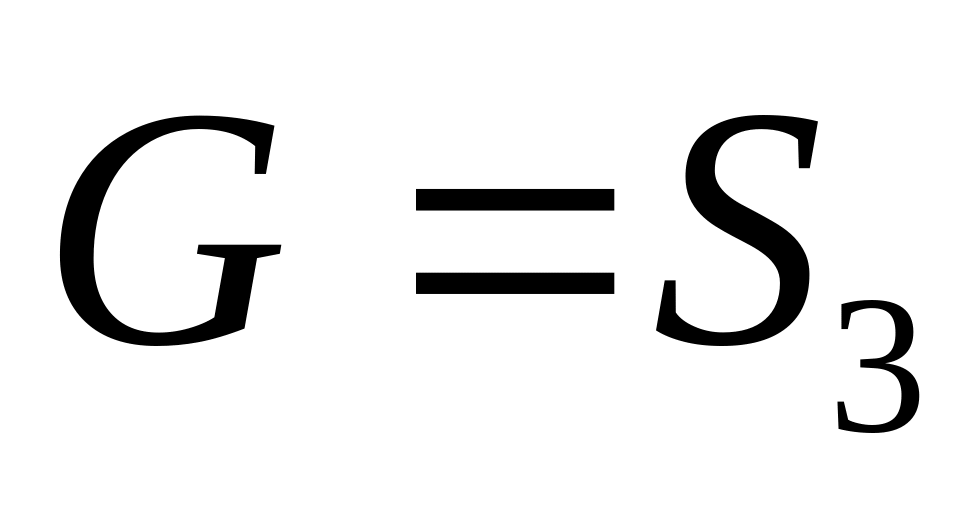 і
і
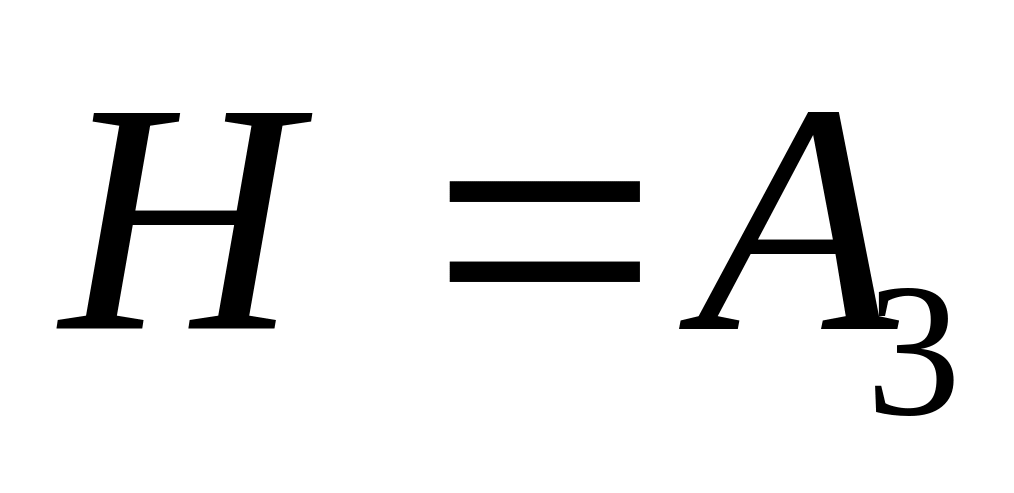 -
підгрупа парних підстановок.
-
підгрупа парних підстановок.
Знайдемо ліві суміжні класи за підгрупою .
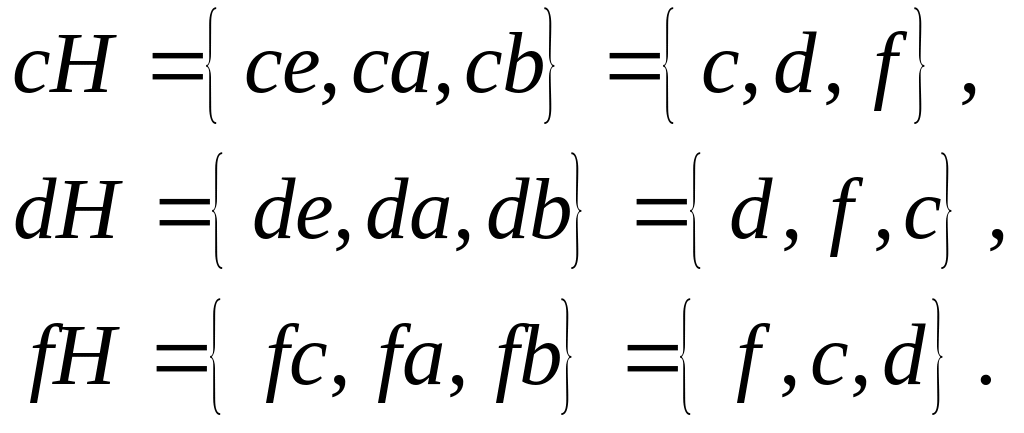
Виявляється
![]() .
.
Наступний приклад показує, що таке спів падіння суміжних класів не є обов'язковим.
Нехай ,
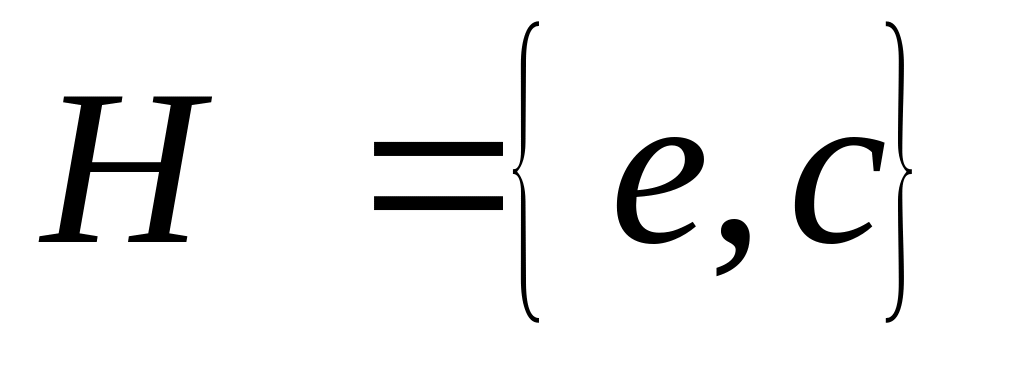 .
Лівий суміжний клас, породжений елементом
d, складається з двох
елементів
.
Лівий суміжний клас, породжений елементом
d, складається з двох
елементів
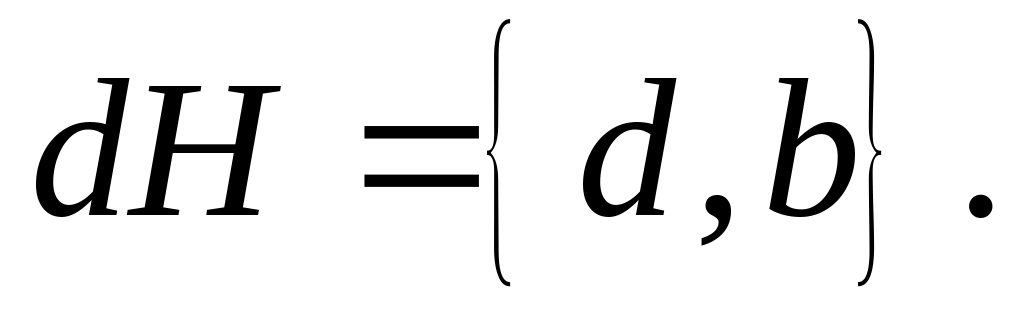 Правий
суміжний клас
Правий
суміжний клас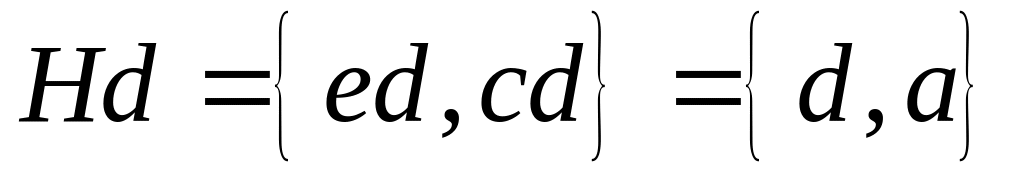 складається також з двох елементів
складається також з двох елементів
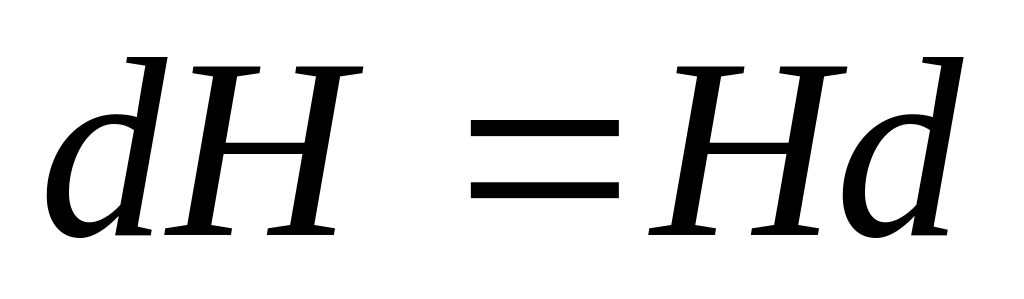 .
.Обчисліть самостійно ліві та праві суміжні класи за підгрупою
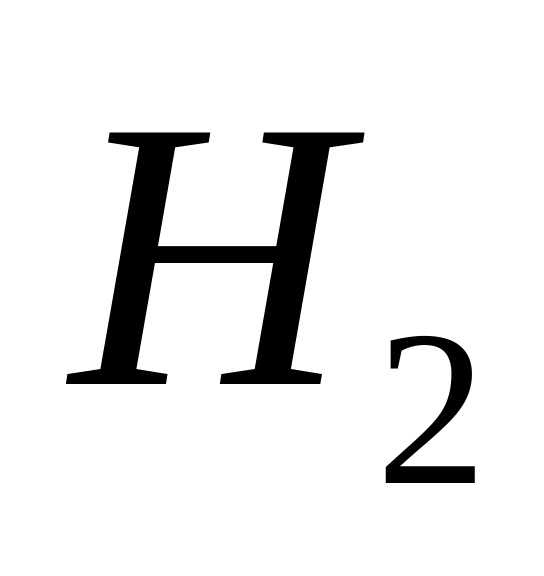 і перевірте, що вони не співпадають.
і перевірте, що вони не співпадають.
