Основні алгебраїчні структури.

Нехай М – довільна множина елементів a, b, c ... Під бінарною алгебраїчною операцією, або алгебраїчною операцією в множині М розуміють закон (правило), за яким будь-яким двом елементам a i b цієї множини ставиться у відповідність єдиний елемент із цієї ж множини.

Тут важливою є вимога однозначності операції і вимога її здійснення для будь-яких двох елементів множини М, а також порядок, у якому беруться елементи множини М під час виконання ними операції. Тобто задати алгебраїчну операцію на множині М означає задати відображення .

Приклад 1.9. Додавання і множення на множині натуральних чисел є алгебраїчними операціями, бо для довільних натуральних чисел a i b їхня сума і добуток визначаються однозначно і є знову натуральними числами. Водночас операції віднімання і ділення не алгебраїчні операції у цій же множині натуральних чисел. Справді, якщо взяти, наприклад, числа 5 і 7 , то не існує таких натуральних чисел p i q , для яких 5-7=р і 5/3=q.

Для позначення довільної алгебраїчної операції, встановленої на множині М, користуватимемося символом *.

Елемент е з множини М називають нейтральним елементом відносно операції * , якщо для будь-якого елемента m з множини М виконується рівність . Нейтральний елемент відносно алгебраїчної операції додавання, визначеної на множині М, називають нулем, а відносно операції множення – одиницею.

Наприклад, на множині цілих чисел число 0 є нейтральним елементом відносно додавання, а число 1 – нейтральним елементом відносно множення.

Елемент а^-1 з множини М називають оберненим елементом до елемента а відносно операції *, якщо . Елемент а^-1, обернений до елемента а відносно операції додавання називають протилежним до а.

Наприклад, у множині цілих чисел відносно операції додавання кожне число а має (обернене ) протилежне число (-а).

Нейтральний елемент є оберненим до себе, бо .

Твердження 1. Якщо відносно операції * на множині М є нейтральний елемент, то він єдиний.

Доведення. Припустимо, що існують два різних нейтральних елемента е₁  е₂. Тоді е₁ =е₁*е₂ = е₂*е₁= е₂. Звідки е₁ = е₂.

Твердження 2. Якщо відносно операції * на множині М для елемента а існує обернений елемент а^-1, то він єдиний.

Доведення. Припустимо, що для елемента а існують два різних обернених елемента а₁^-1  а₂^-1. Тоді а₁^-1 = е* а₁^-1 = а*а₂^-1* а₁^-1 = а₂^-1. Звідки а₁^-1 = а₂^-1.

А

	а	b	…	y	…	d
a	aa	ab	…	ay	…	ad
b	ba	bb	…	by	…	bd
…	…	…	…	…	…	…
x	xa	xb	…	xy	…	xd
…	…	…	…	…	…	…
d	da	db	…	dy	…	dd

мал.2.1.

лгебраїчні операції можуть мати наступні властивості:

1. Асоціативність : для будь-яких елементів а, b і с з М виконується рівність .

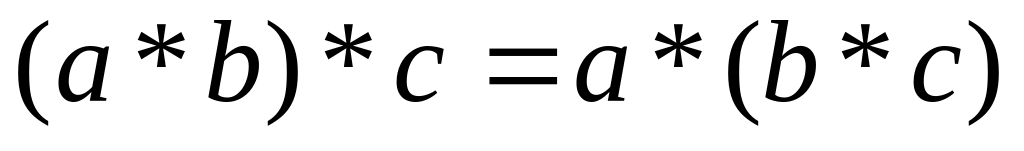2. Існування нейтрального елемента е з М.

3. Існування оберненого елемента а^-1 з М для будь-якого елемента а з М.

4. Комутативність : для будь-яких елементів а і b з М виконується рівність .

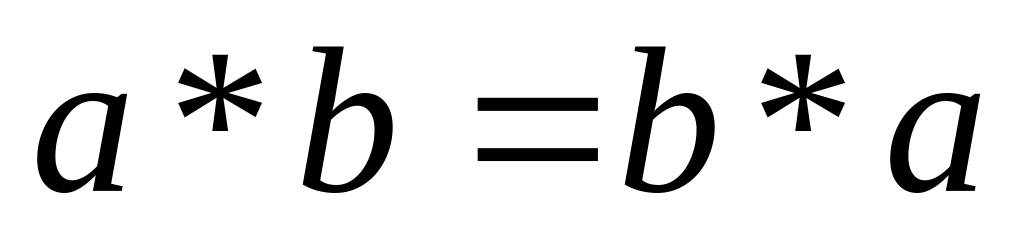Результат виконання алгебраїчної операції на скінченній множині часто задають за допомогою таблиць Келі. Ці таблиці нагадують таблицю множення чисел. Щоб побудувати таблицю Келі для множини М={a, b, …, d} випишемо у стовпчик і у рядок угорі всі елементи множини М, додержуючи одного і того ж порядку, а результат операці x*y - на перетині рядка, який відповідає елементу x та стовпчика, який відповідає елементу y (мал.2.1).

Приклад 1.10. Скласти таблицю Келі групи підстановок множини трьох елементів.

Розв'язок. Введемо позначення:

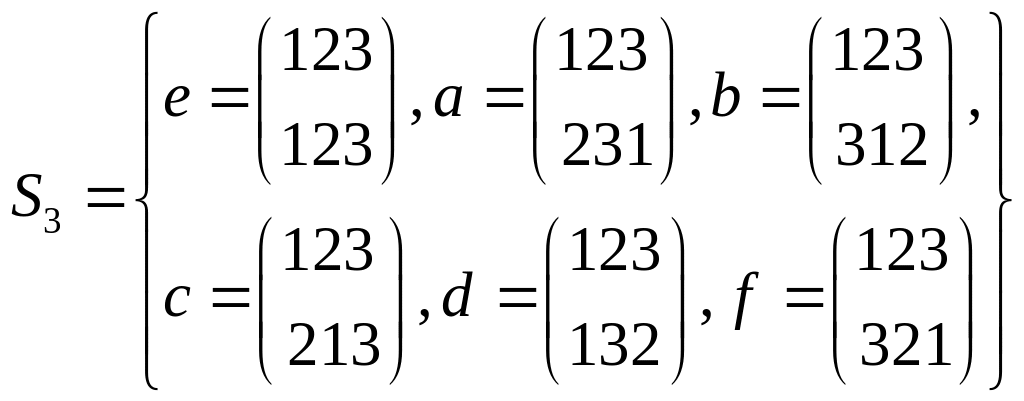
Тоді таблиця Келі групи така:

	e	a	b	c	d	f
e	e	a	b	c	d	f
a	a	b	e	f	c	d
b	b	e	a	d	f	c
c	c	d	f	e	a	b
d	d	f	c	b	e	a
f	f	c	d	a	b	e

Тому, що

Приклад 1.11. Нехай - множина неперервних функцій на множині R. Поставимо у відповідність кожній парі ( ) елементів в С(R) таку функцію яка в кожній точці приймає значення f(x) + g(x) , де “+” означає звичайне додавання дійсних чисел. Це можна записати так:

Оскільки сума неперервних функцій є функція неперервна , то – алгебраїчна операція.

Приклад 1.12. Розглянемо множину . . Задамо алгебраїчну операцію на цій множині так: якщо то + = тобто, сума двох класів еквівалентності є клас еквівалентності, що містить . Пояснимо це докладніше. Щоб додати цілі числа, і за модулем m ( тобто знайти суму ) потрібно спочатку додати їх, а потім знайти остачу від ділення цієї суми на число m. Якщо , то і + = Наприклад, коли m=5 то 3+4=2 ( ) , бо і , отже, + в множині . Далі позначатимемо множину Через .

Приклад 1.13. Нехай дано два відображення та ( множини X, Y, Z - довільні ). Композицією ( добутком ) відображень f і g називається таке відображення Інакше кажучи, під композицією відображень розуміємо їх послідовне виконання. Позначимо через S(X) множину всіх сюр’єктивних відображень множини X на себе. На S(X) композиція відображень є алгебраїчною операцією.

ГРУПА.

Непорожня множина G називається групою відносно операції *, якщо виконуються такі властивості (аксіоми групи):

1. Операція * є алгебраїчною на множині G, тобто

: .

2. Операція * є асоціативною, тобто .

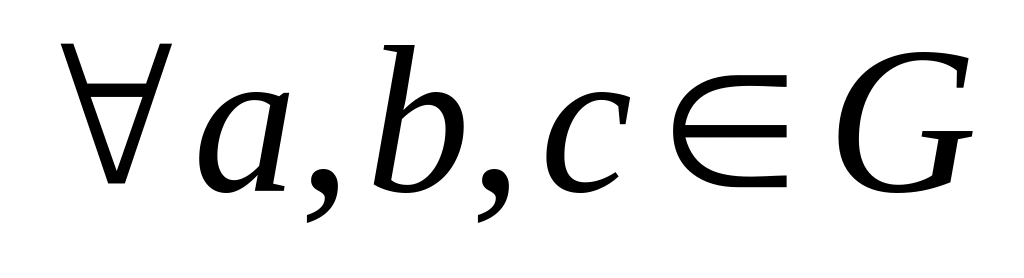
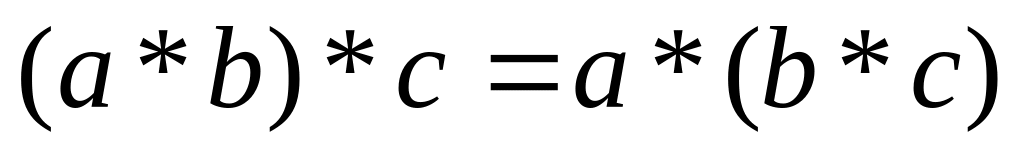3. У множині G існує нейтральний елемент відносно операції *, тобто .

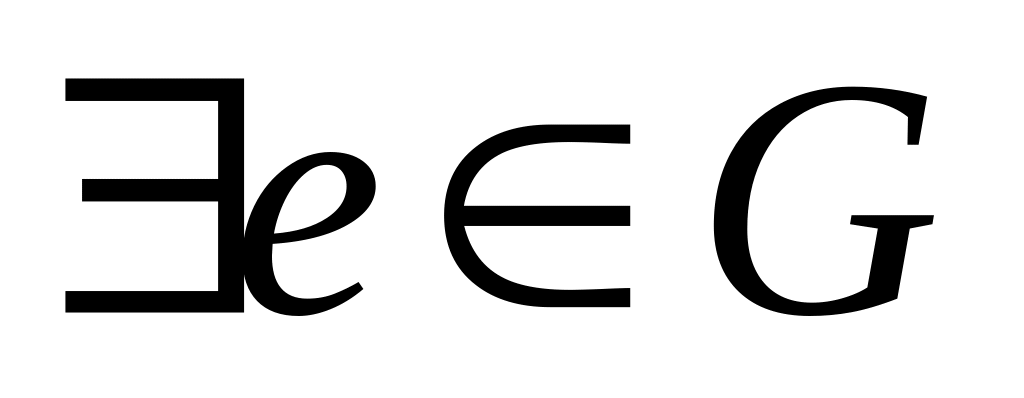
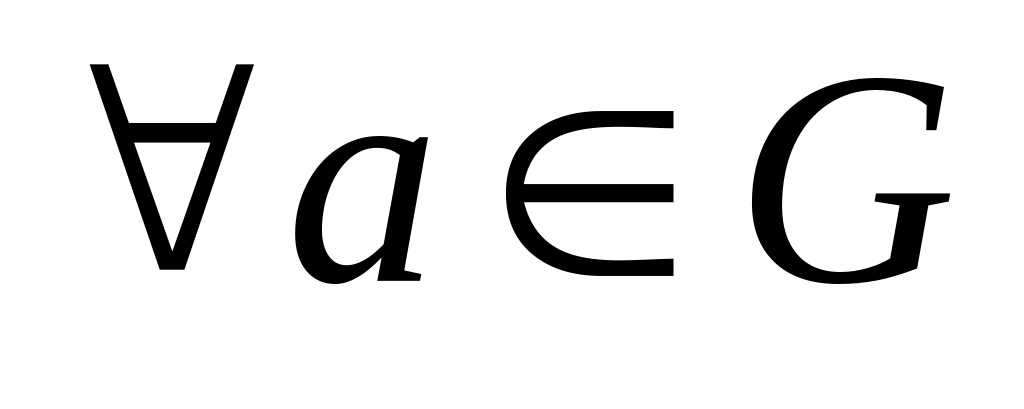
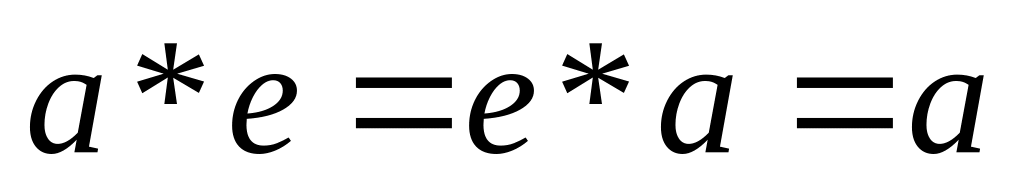4. У множині G для будь-якого її елемента існує обернений елемент, тобто .

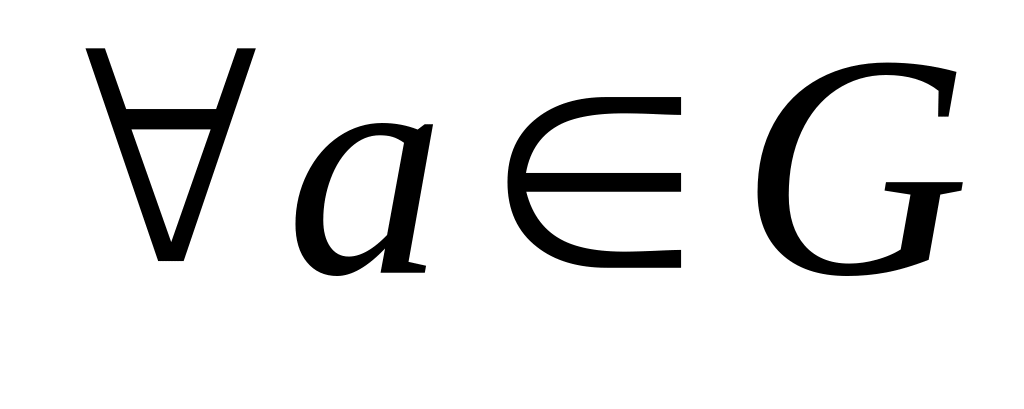
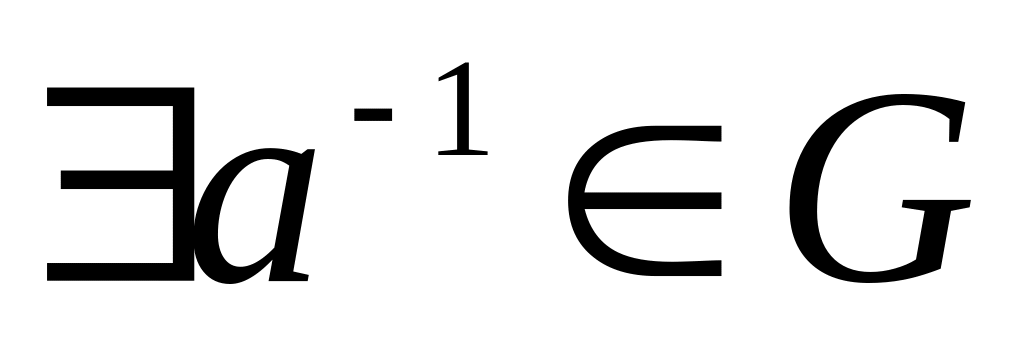
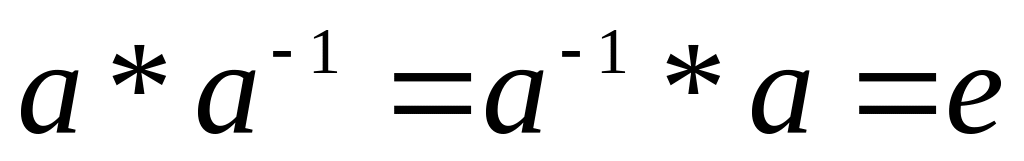Приклад 1.14. Множина всіх цілих чисел відносно операції додавання є групою, а відносно операції множення ця сама множина не є групою. Справді, операції додавання та множення на множині цілих чисел є алгебраїчними (сумою (добутком) будь-яких двох цілих чисел є відповідне ціле число) та асоціативними ( , ). Роль нейтрального елемента відносно додавання відіграє ціле число 0, а відносно множення - число 1. Оберненим для числа а відносно додавання у множині цілих чисел є протилежне число (-а). А відносно множення обернені елементи існують у множині цілих чисел лише для 1 та -1.

З аксіом груп випливають такі властивості:

Твердження 1. виконується закон скорочення:

- ліве скорочення,

- праве скорочення.

Доведення. Дійсно, якщо , то і , звідки . Отримали . Аналогічно для маємо .

Твердження 2. Для кожної пари елементів існують єдині розв’язки рівнянь та - і .

Єдність розв’язків випливає з законів скорочення.

Група називається скінченною, якщо вона має скінченне число елементів, у протилежному випадку група називається нескінченною. Кількість елементів скінченої групи називається її порядком.

Групу відносно операції множення називають мультиплікативною (від латинського слова multiplication – множення), а відносно операції додавання - адитивною (від латинського слова addition – додавання) групою.

Приклад 1.15. Перевіримо, чи множина підстановок n-го степеня є групою:

1. Операція множення підстановок n-го степеня є алгебраїчною, оскільки будь-яким двом підстановкам f i g n-го степеня ставиться у відповідність єдина підстановка n-го степеня.

2. Операція множення підстановок n-го степеня є асоціативною:

3. У множині підстановок n-го степеня існує нейтральний елемент відносно операції множення підстановок – тотожня підстановка.

4. У множині підстановок n-го степеня для будь-якого її елемента існує обернений елемент – обернена підстановка.

Група підстановок n-го степеня називається симетричною групою степеня n і позначається S_n.

Приклад 1.16. Перевірити, чи є асоціативною операція композиції відображень на множині S(X) .

Нехай , відображення. Для всіх маємо:

Отже, . Тому операція композиції відображень на множині S(X) асоціативна.

Приклад 1.17. Перевірити, чи є асоціативною алгебраїчна операція Т на множині R , яка кожній парі (a, b) ставить у відповідність середнє арифметичне чисел a і b. Тобто . Дійсно

Якщо , то

Приклад 1.18. Перевірити, чи є групою множина матриць , де і відносно операції множення матриць.

Дійсно, добуток матриць такого виду знову буде матриця такого ж виду :

=

Нейтральним елементом є одинична матриця, яка одержується при

Обернена матриця існує для кожної матриці такого ж виду :

=

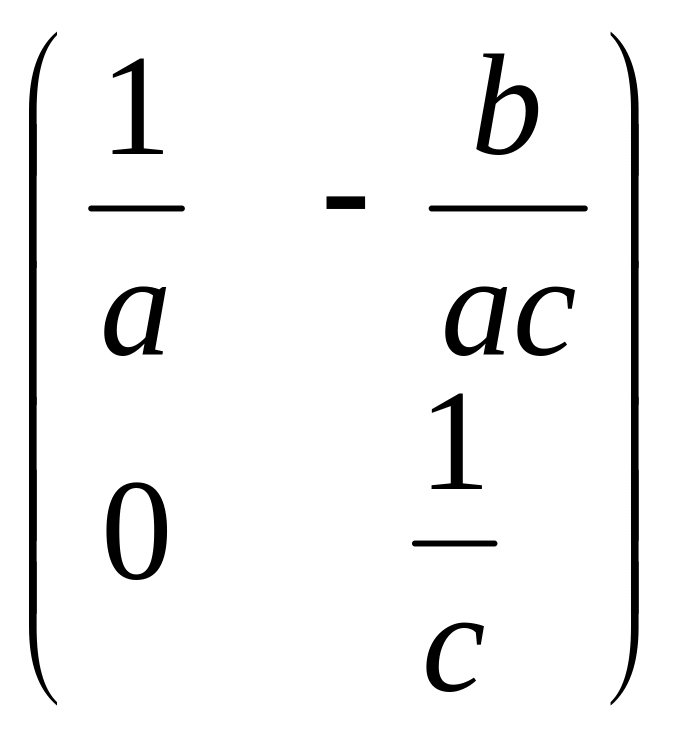Отже, якщо = , то

Це група не комутативна, бо

=

Приклад 1.19. Довести, що множина є абелевою групою відносно додавання за модулем n.

Дійсно ця операція є алгебраїчною та асоціативною, а нейтральним елементом є бо

Оберненим до елемента є елемент , бо . Ясно , що в операція додавання за модулем n комунікативна.

Приклад 1.20. Чи утворює групу множина , якщо на ній операцію Т визначити так:

Розв'язок. Перевіримо асоціативний закон:

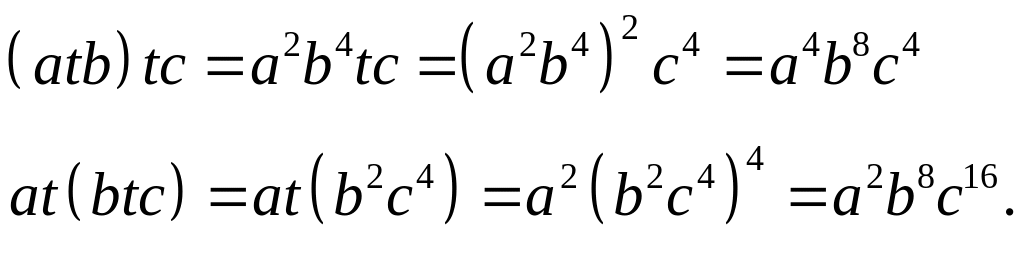
Таким чином . І множина відносно так визначеної операції Т групи не утворює.

Приклад 1.21. Чи утворює групу множина , якщо операцію визначити так:

Розв'язок. Асоціативний закон:

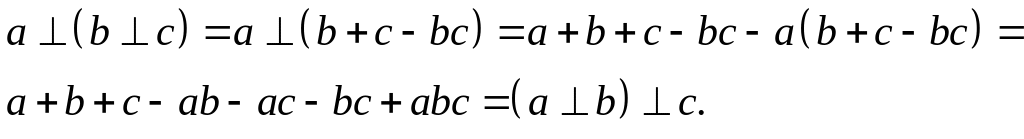
Існування нейтрального елемента:

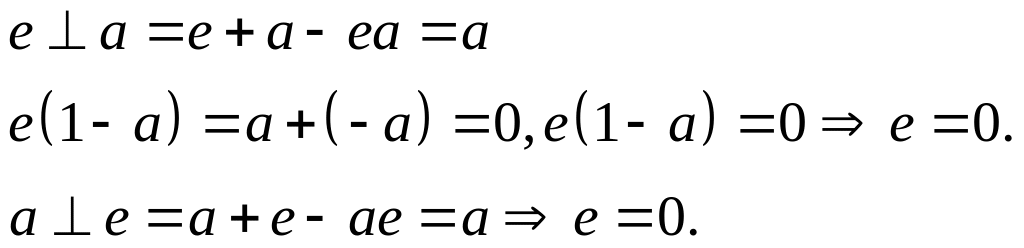
Існування оберненого елемента:

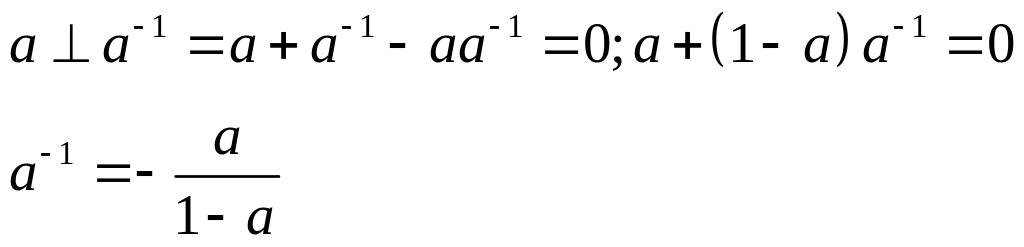
Оскільки для 1Є не існує оберненого елемента, то групи не утворює відносно операції .

Приклад 1.22. Довести, що

а) в довільній групі

б) .

Розв'язок.

а) Дійсно,

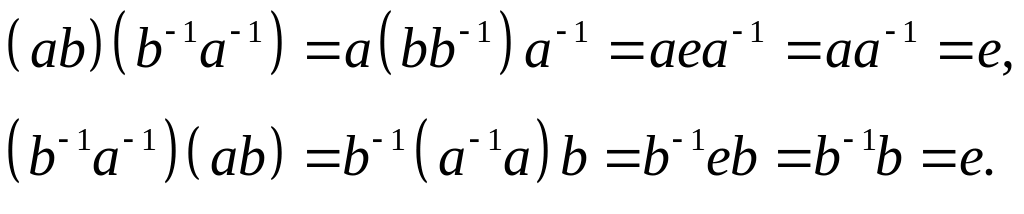
Так як обернений елемент єдиний, то а) доведено. Пункт б) пропонуємо довести читачеві самостійно, використавши метод математичної індукції.

Приклад 1.23. Нехай для довільного елемента групи довести, що група комутативна.

Розв'язок. Так як для довільного елемента то для будь-яких елементів і маємо .

Помножимо обидві частини цієї нерівності зліва на і справа на . Одержимо:

Так як і , то і . Але і довільні елементи групи , тому група - абелева.