Співставлення поступального та обертального рухів

Метою даного теоретичного вступу було встановлення досить глибокої аналогії між поступальним та обертальним рухами. В табл.1 співставленні основні величини і рівняння поступального руху і обертання навколо нерухомої осі.

Таблиця 2.1

Поступальний рух	Обертальний рух
- лінійна швидкість	- кутова швидкість
- лінійне прискорення	- кутове прискорення
- маса	- момент інерції
- імпульс	- момент імпульсу
- сила	- момент сили
- рівняння динаміки	- рівняння динаміки
- рівняння динаміки	- рівняння динаміки
- кінетична енергія	- кінетична енергія

Із цього співставлення випливає, що відповідають один одному швидкість і кутова швидкість , прискорення і кутове прискорення . Роль маси т відіграє момент інерції , роль імпульсу – момент імпульсу , сили – момент сили . Отже, основні рівняння поступального і обертального рухів співпадають по формі.

Опис лабораторної установки

Маятник Обербека складається з чотирьох стержнів, закріплених на втулці під прямим кутом один до одного (рис. 2.10).

Втулка з шківом радіуса насаджена на вісь в підшипниках так, що вся система може обертатися навколо горизонтальної осі. Момент інерції приладу можна змінювати, пересуваючи тягарці вздовж стержнів. На шків намотана тонка нитка. Прив'язана до неї платформа т служить для розміщення вантажів.

Основний закон динаміки для обертальної системи має вигляд:

,

де М - сумарний момент сил, діючий на обертальну систему; - кутове прискорення системи; - момент інерції обертальної системи.

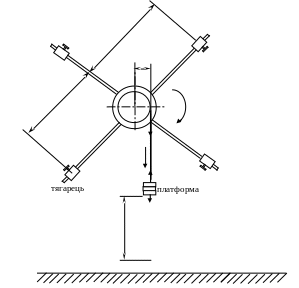
Рис.2.10

Обертаючий момент створюється силою натягу нитки Т:

,

де - радіус шківа. Силу Т можна знайти з рівняння руху платформи з вантажами:

.

Тут т - маса платформи з вантажами; а - прискорення платформи; - прискорення вільного падіння.

Звідси знаходимо :

.

В підшипниках, які забезпечують обертання, діє момент тертя М_тр , прикладений також до осі обертання маятника і направлений протилежно обертальному моменту М_н.. Тому, в загальному випадку,

М=М_н-М_тр.

Однак момент тертя М_тр малий в порівнянні з моментом сили натягу нитки М_н (у лабораторній установці використовуються підшипники, у яких М_тр =0,01М_н). Отже, при виведенні розрахункових формул дією цього моменту будемо нехтувати, вважаючи, що М =М_н.

Вимірюючи час , протягом якого навантажена платформа із стану спокою спускається на відстань , можна знайти її прискорення .

Нитка тонка і змотується зі шківа маятника без тертя і ковзання, тому лінійне прискорення точок його поверхні також дорівнює а. Кутове прискорення шківа пов'язане з лінійним прискоренням співвідношенням , звідки

.

Основний закон динаміки для даної системи можна записати у вигляді:

.

Підставимо отримані значення , , в це рівняння і розв’яжемо його відносно . Дістанемо вираз для моменту інерції системи:

(3)

Для визначення моменту інерції треба знайти дослідним шляхом усі величини, що стоять у правій частині отриманої формули (прискорення вільного падіння відоме). Тобто необхідно знайти масу платформи з вантажами т, яка приводить систему в рух, радіус шківа , час опускання маси т від верхньої точки до нижньої, виміряти шлях , який платформа проходить при опусканні.

Момент інерції всієї системи складається з моменту інерції - системи без тягарців і моменту інерції чотирьох тягарців , які закріплені на стержнях.

В першому наближенні тягарці можна прийняти за точкові, тоді момент інерції одного з них можна визначити за формулою:

,

де - маса тягарця;

- віддаль від осі обертання до центра мас тягарця.

Тоді момент інерції всієї системи можна обчислити за формулою:

(4)

В результаті експерименту, використовуючи формулу (2.1), можна окремо визначити момент інерції всієї системи, що обертається з масами . Потім, знявши маси, аналогічно визначимо момент інерції , тобто системи без мас . З виразу (4) знайдемо, що

_.

Звідки _. Таким чином, момент інерції одного тягарця можна визначити експериментально за формулою:

_.

Тут індекс е означає, що значення отримано експериментально.