Визначення коефіцієнта в’язкості за методом Стокса

Англійський фізик і математик Д.Стокс (1814-1903) досліджував характер сил що діють на тіла що рухаються в рідині і виявив що при невеликих швидкостях руху опір середовища зумовлений практично тільки силами внутрішнього тертя. Сила опору при русі твердого тіла пропорційна швидкості тіла . Коефіцієнт пропорційності залежить від форми тіла і пропорційний в’язкості рідини і лінійним розмірам тіла. Стокс встановив, що для невеликих кульок, сила опору руху в рідинах дорівнює

,

де - в'язкість рідини, швидкість руху кульки, радіус кульки.

Рис.5.3

Розглянемо сили, що діють на кульку в рідині. На рис.5.1 показані три сили: сила тяжіння , виштовхуюча сила Архімеда і сила опору ,яку називають силою Стокса. Основний закон динаміки поступального руху кульки .

В проекції навісь :

. (5.2)

З трьох сил тільки одна є змінною – це сила опору . Дійсно, сила опору пропорційна швидкості кульки, тому спочатку руху швидкість почне зростати. Сила опору ( ) також буде зростати, а прискорення буде зменшуватись і наступить такий момент, коли прискорення стане дорівнювати нулю. Починаючи з цього моменту кулька буде рухатись рівномірно. Тобто падіння кульки спочатку буде прискореним, а далі кулька рухається з сталою швидкістю ( ). Рівняння руху (5.2) буде мати вид:

Звідки:

(5.3)

За законом Архімеда виштовхувальна сила дорівнює вазі рідини, яка витісняється кулькою. Об'єм кульки - густина рідини - , тому маса рідини яку витісняє кулька а сила Архімеда Маса кульки може бути знайдена за формулою де - густина матеріалу кульки, а сила тяжіння тоді дорівнює . Підставимо отримані значення сил у рівняння (5.3)

Звідки в'язкість:

. (5.4)

Швидкість з якою рухається кулька можна знайти за формулою де - відстань між двома мітками на посудині, а - час, за який кулька проходить цю відстань. Враховуючи, що зручніше вимірювати діаметр кульки , формулу (5.4 ) можна записати у вигляді:

. (5.5)

Завдання роботи

1. Розібратися з фізичною сутністю в'язкості рідин і особливостями руху твердого тіла у в'язкому середовищі.

2. Визначити коефіцієнт в'язкості рідини за методом Стокса.

Виконання роботи

Прилади та матеріали: посудина з досліджуваною рідиною, свинцеві кульки, масштабна лінійка, секундомір, термометр.

Опис установки

Для визначення в'язкості за методом Стокса використовують високий циліндричний посуд з досліджуваною рідиною рис.5.3. Зверху циліндр закритий кришкою з отвором посередині, куди кидають кульку. На посуді є дві кільцеві мітки А і В. Мітка А відповідає тієї висоті, де сили, що діють на кульку урівноважуються і рух її стає рівномірним. Нижня мітка В нанесена для зручності відліку часу.

1. Виміряти 3 рази відстань між мітками на скляному циліндрі за допомогою масштабної лінійки.

2. Визначити середнє значення і записати його до таблиці.

3. Виміряти 3 рази в різних місцях діаметр кульки за допомогою мікрометра.

4. Знайти середнє значення діаметра 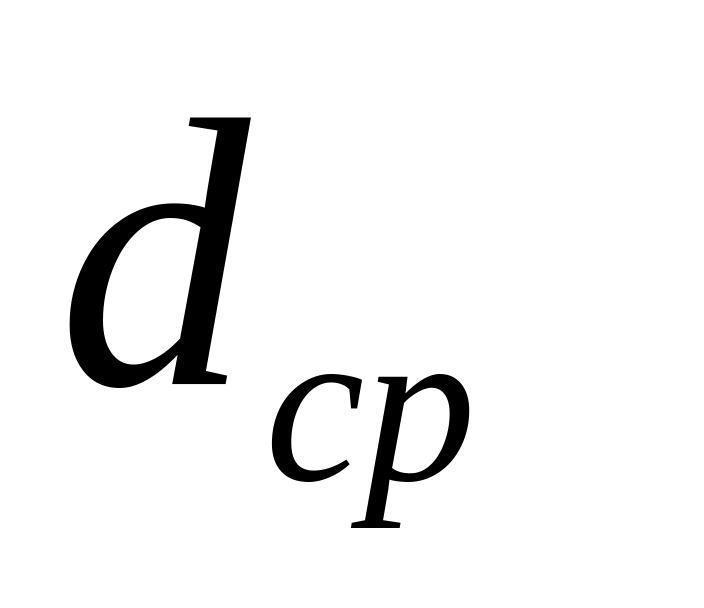і записати його до таблиці.

5. Підготувати до вимірювання секундомір.

6. Опустити кульку в циліндр і виміряти час, за який кулька проходить відстань між мітками. Результати вимірювань записати до таблиці.

7. Взяти ще дві кульки і провести аналогічні вимірювання, записуючи результати до таблиці.

8. За формулою (5.5) розрахувати коефіцієнти в'язкості за результатами вимірювань.

9. Розрахувати середнє значення , середню абсолютну і середню відносну похибку .

10. Записати кінцевий результат у вигляді:

Температура суттєво впливає на коефіцієнт внутрішнього тертя, тому слід записати у звіт температуру, при якій проводився дослід.

Таблиця 5

№
1
2
3
Ср.

Контрольні запитання

1. Що таке сила внутрішнього тертя?

2. Записати формулу сили внутрішнього тертя і пояснити її фізичний зміст.

3. Які сили діють на кульку, яка рухається в рідині?

4. Вивести формулу для визначення коефіцієнта в'язкості за методом Стокса.

5. Яка залежність в'язкості рідини від температури?

6. Лабораторна робота № 5

ВИЗНАЧЕННЯ КОНЦЕНТРАЦІЇ ЦУКРУ В РОЗЧИНІ ЗА КУТОМ ОБЕРТАННЯ ПЛОЩИНИ ПОЛЯРИЗАЦІЇ

Дуалізм хвиль та частинок

Світло являє собою складне явище: в одних випадках воно веде себе як електромагнітна хвиля, в інших - як потік особливих частинок (фотонів). Говорять, що світло володіє одночасно і хвильовими і корпускулярними властивостями.

Аналізуючи явища інтерференції, дифракції та поляризації світла ми підкреслюємо хвильову природу світла. Розглядаючи явище фотоефекту, уявляємо світловий потік у вигляді потоку частинок - фотонів.

По сучасним уявленням не тільки електромагнітне випромінювання має властивості хвиль і властивості частинок, але й будь-яка мікроскопічна частинка, наприклад електрон, має як корпускулярні, так і хвильові властивості. Встановлено, що рухові частинки можна співставити хвилю, довжиною , де - стала Планка, р – імпульс частинки. Енергія частинки Е пов'язана з частотою співвідношенням . Корпускулярні та хвильові властивості частинок невід'ємні одна від одної. Очевидно, не існує частинок, які володіють тільки корпускулярними, або тільки хвильовими властивостями. Виходячи з цього, був відкритий фундаментальний закон природи, який називається дуалізмом хвиль та частинок, або корпускулярно-хвильовим дуалізмом.

Явища, пов'язані з поляризацією світла розглядаються на основі хвильових властивостей світла. Тому, не розглядаючи корпускулярних уявлень, будемо вважати, що світло являє собою електромагнітну хвилю.