3. Оценка надежности программного обеспечения
Постановка задачи.
Бурное развитие компьютерных технологий привело к их широкому использованию как в составе автоматизированных средств контроля так и непосредственно для управления работой различных технических систем. В связи с этим растут объемы программного обеспечения (ПО) и соответственно ужесточаются требования к надежности функционирования компьютерных программ. По сравнению с традиционным подходом решение задачи обеспечения надежности ПО усложняется, так как причины нештатных ситуаций становятся более разнообразными. В частности, они обуславливаются как отказами элементов технических устройств, так и ошибками в записи программ и сбоями в их работе. При проведении технического обслуживания (ТО) работоспособность ПО оценивается по результатам тестирования ПО, во время которого определенное число ошибок исправляется. Процесс тестирования состоит из ряда этапов:
выполнение программы тестирования; обнаружение ошибки; устранение ошибки;
продолжение работы программы. В процессе тестирования регистрируются отказы, возникающие при работе ПО в течении каждого сеанса тестирования. Информация о выявленном количестве отказов на различных сеансах тестирования используется для оценка показателей надежности ПО. Для решения этой задачи могут быть использованы различные модели прогнозирования надежности. В дальнейшем рассмотрим некоторые из них.
Аналитическая модель прогнозирования надежности ПО.
Существующие модели оценки надежности ПО основаны на использовании неоднородного пуассоновского процесса (НПП). При этом принимается, что математическое ожидание числа выявленных ошибок имеет экспоненциальный рост. Однако на практике , как правило, число выявленных ошибок подчиняется S-образной кривой. В дальнейшем эта гипотеза будет подтверждена при рассмотрении механизма формирования отказов в процессе проведения проверок с заменой отказавших элементов на каждом цикле тестирования. В данном разделе анализируется следующий вид этой зависимости , предложенной в работе [7]
,
где M(t) – математическое ожидание числа выявленных ошибок за время t ;
a,b – коэффициенты аппроксимации;
t – время функционирования устройства.
При решении задачи предполагается, что ошибки, выявляемые на каждом цикле тестирования, устраняются по мере их обнаружения. При этом новых ошибок не вносится.
В соответствии с анализируемой моделью , надежность ПО оценивается по соотношению
,
где P(t,s) – вероятность того, что в интервале ( s, s+t ) не встретится никаких ошибок ПО при условии, что последняя ошибка выявлена и устранена в момент s.
Оценка
параметров a и b
исследуемой модели производится по
результатам тестирования. В дальнейшем
представим статистические данные о
тестировании в виде значений
,
которые характеризуют количество ошибок
ПО, выявленных к моменту времени
.
Для нахождения искомых параметров воспользуемся методом максимального правдоподобия. В общем случае функция правдоподобия имеет вид
,
где
вектор искомых параметров;
результаты тестирования.
В
рассматриваемом случае
характеризует вероятность появления
именно столько ошибок, сколько
реализовалось на каждом цикле тестирования.
Согласно принятому предположению эта
вероятность подчиняется НПП с s-образным
изменением математического ожидания.
Таким образом выражение для функции
правдоподобия примет вид
,
где
После подстановки получим
Производя логарифмирование, получим
,,
где
.
Очевидно
.
Искомые параметры должны удовлетворять условию оптимальности
.
Производя дифференцирование по параметру a , получим
Отсюда
Разрешая соотношение относительно a, приходим к искомой оценке
(1)
Дифференцируя логарифм функции правдоподобия по параметру b будем иметь
,
где
;
Подставляя полученные соотношения в условие оптимальности, найдем
С учетом соотношения, полученным выше, для оценки параметра a , окончательно будем иметь
,
где
.
Для иллюстрации работоспособности предлагаемого подхода рассмотрим модельный пример.
При решении задачи предположим, что за 10 сеансов тестирования была выявлена 31 ошибка. Результаты тестирования по каждому циклу представлены ниже:
где
накопленное количество ошибок,
соответствующее i-тому
циклу тестирования.
Искомые значения b оценивались графически при выполнении условия
(2)
Графическое решение этого уравнения представлено на рис. 1
Рис.
1 Изменение функции Ф(x)
и функции
по параметру x=b.
При построении графика было принято обозначение: x=b .
Как видно из графика условие (2) удовлетворяется при значении b = 0.345.
В дальнейшем по соотношению (1) оценивается значение параметра a
.
Знание
a и b
позволяет найти распределение
прогнозируемых значений числа ошибок
по циклам тестирования i
Результаты расчета представлены на рис. 2
Рис. 2 Распределение расчетных оценок M(i) и реального накопления ошибок N(i)
по циклам тестирования i .
При формировании накопленного при тестировании количества ошибок N(i) для сеансов , по которым отсутствуют опытные данные (i=11-15), с целью построения графика, условно принято значение минус 360.
Характер изменения математического ожидания число ошибок M(i) по циклам тестирования представлен на рис.3
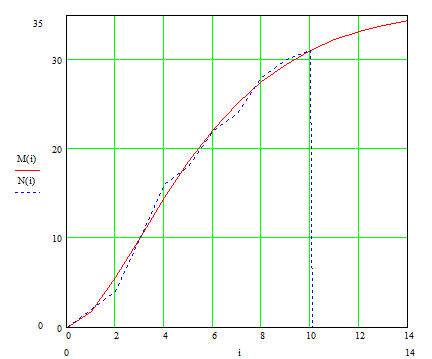
Рис. 3 Характер изменения сглаживающей кривой M(i) и экспериментальной
кривой N(i) по числу циклов тестирования i .
На графиках по оси абсцисс отложены циклы тестирования, а по оси ординат – число выявленных ошибок. Реальное накопление ошибок представлено пунктирной кривой N(i) . Обе кривые имеют слабо выраженную S—образную форму. Как видно из графика аппроксимирующая кривая хорошо согласуется с опытными данными.
Использование метода наименьших квадратов в задачах
обеспечения надежности технических систнм.
Анализ стратегии технического обслуживания по состоянию.
Перспективным направлением организации технического обслуживания является эксплуатация систем по состоянию, которая предполагает периодический контроль и измерение параметров, определяющих техническое состояние изделий. При этом решение о замене или восстановлении работоспособности изделия принимается тогда, когда значение параметров работоспособности достигают критического уровня соответствующего отказу.
Для анализа предлагаемого подхода проанализируем возможные реализации монотонно возрастающего случайного процесса. Очевидно, достижение допустимого уровня приводит к отказу устройства. Следовательно останавливать наблюдение и проводить замену необходимо до достижения критического уровня. В дальнейшем решим задачу отыскания оптимального момента замены системы по информации о поведении конкретной реализации процесса. Допустим, что после проведения «i» наблюдений известно, что изделие находится в работоспособном состоянии. Для решения вопроса о целесообразности его замены нужно оценить работоспособность системы на (i + 1) – ом шаге ее функционирования.
Таким образом возникает задача прогнозирования поведения случайного процесса y(t) на (i +1) – ом шаге по результатам измерений в предшествующие моменты времени. Существуют различные методы прогнозирования случайных процессов .
В дальнейшем остановимся на методе наименьших квадратов, нашедшем широкое применение в инженерной практике.
При решении задачи будем предполагать, что случайная функция может быть представлена в виде
или в матричной форме
(1 )
где
- вектор значений функции;
- матрица известных координат;
- вектор неизвестных параметров;
n – число измерений;
K – число неизвестных параметров.
С учетом случайных воздействий уравнение (1) примет вид
где
- вектор измерений;
- вектор случайных воздействий.
Согласно
методу наименьших квадратов оценки
неизвестных параметров
удовлетворяют соотношению
Точность оценок определяется дисперсионной матрицей
где
- дисперсия случайных воздействий
.
При отсутствии априорной информации о статистических свойствах случайных воздействий, неизвестную дисперсию можно оценить по соотношению
где
- остаточная сумма квадратов.
Очевидно
Полученные результаты
могут быть применены для получения
доверительного интервала, содержащего
последующее (n+1) – ое
значение
величины y. Если
заданные значения регрессоров,
соответствующие значению
,
то несмещенная оценка математического
ожидания
будет равна
, где
Поскольку
имеет дисперсию
,
то дисперсия
увеличивается
на эту величину, то-есть
Подставляя
вместо
приходим к статистике Стьюдента
Очевидно верхняя граница доверительного интервала для значения удовлетворяет условию
,
где уровень доверительной вероятности.
Вычитая из обоих частей
неравенства значение
и деля на среднее квадратическое
отклонение разности
, получим
Разность подчиняется нормальному распределению с нулевым математическим ожиданием. Поэтому левая часть неравенства подчиняется распределению Стьюдента. Таким образом соотношение примет вид
,
где
аргумент функции распределения Стьюдента,
соответствующий уровню доверительной
вероятности
.
Приравнивая аргументы , входящие в левую и правую часть равенства, получим
Разрешая соотношение
относительно искомого параметра
,
окончательно получим
,
где
.
Для иллюстрации эффективности рассматриваемого подхода оценим периодичность замен для примера, рассмотренного в предыдущем разделе .При проведении расчетов
предположим, что производится периодический контроль параметров работоспособности устройства. Результаты предполагаемых измерений представлены в табл. 1. .
Результаты измерений Таблица 1
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
y |
1 |
1.15 |
1.2 |
1.25 |
1.4 |
1.5 |
1.6 |
1.65 |
1.8 |
По результатам, представленным в табл..1 проводилась оценка параметров аппроксимирующей прямой
Согласно предлагаемому подходу, после каждого n – го испытания проводится расчет
коэффициентов аппроксимации. Знание этих коэффициентов позволяет определить
прогнозируемые
значения параметра работоспособности
на n+1 – ом шаге и верхнюю
границу доверительного интервала для
этого параметра
на n+1 – ом шаге
Расчеты проводились по программе Matchad по соотношениям
где
Параметр t
оценивается по таблице квантилей
распределения Стьюдента (см. табл. .2 ) .
Для заданного
величина
определялась для числа степеней свободы
f= n-2, где
n –текущий объем выборки;
.Результаты
расчетов проводимых после ,4,5,6,7,8,9
испытаний представлены на рис. 1-6
Квантили распределения Стьюдента Таблица.2
f |
|
f |
|
|||||||
0,8 |
0,9 |
0,95 |
0,98 |
0,8 |
0,9 |
0,95 |
0,98 |
|||
1 |
3,07 |
6,31 |
12,70 |
31,82 |
14 |
1,345 |
1,761 |
2,145 |
2,624 |
|
2 |
1,88 |
2,92 |
4,30 |
6,69 |
15 |
1,341 |
1,753 |
2,131 |
2,602 |
|
3 |
1,63 |
2,35 |
3.18 |
4,54 |
16 |
1,337 |
1,746 |
2,120 |
2,583 |
|
4 |
1,53 |
2,13 |
2,77 |
3,74 |
17 |
1,333 |
1,740 |
2,110 |
2,567 |
|
5 |
1,47 |
2,01 |
2,57 |
3,36 |
18 |
1,330 |
1,734 |
2,101 |
2,552 |
|
6 |
1,44 |
1,94 |
2,44 |
3,14 |
19 |
1,328 |
1,729 |
2,093 |
2,539 |
|
7 |
1,41 |
1,89 |
2,36 |
2,99 |
20 |
1,325 |
1,725 |
2,086 |
2,528 |
|
8 |
1,39 |
1,86 |
2,30 |
2,89 |
21 |
1,323 |
1,721 |
2,080 |
2,518 |
|
9 |
1,38 |
1,83 |
2,26 |
2,82 |
22 |
1,321 |
1,717 |
2,074 |
2,508 |
|
10 |
1,37 |
1,81 |
2,22 |
2,76 |
23 |
1,319 |
1,714 |
2,069 |
2,500 |
|
11 |
1,36 |
1,79 |
2,20 |
2,71 |
24 |
1,318 |
1,711 |
2,064 |
2,492 |
|
12 |
1,356 |
1,78 |
2,17 |
2,68 |
25 |
1,316 |
1,708 |
2,059 |
2,485 |
|
13 |
1,35 |
1,77 |
2,16 |
2,65 |
26 |
1,315 |
1,706 |
2,056 |
2,479 |
|
Рис. .1 Результаты расчетов ( n=4 )
Рис. 2 Результаты расчетов ( n=5 )
Рис. 3 Результаты расчетов ( n= 6 )
Рис. 4 Результаты расчетов ( n=7 )
Рис. 5 Результаты расчетов ( n=8 )
Рис. 6 Результаты расчетов (n=9).
В результате проведения расчетов были найдены прогнозируемые значения параметров работоспособности и верхние границы их доверительных интервалов представленные на рис. 1
Рис. 1 Изменение прогнозируемых
значений
(
кривая F(x))
и
верхней границы доверительного
интервала
( кривая
,
для .
Как видно из графика, для принятых
исходных данных, верхняя граница
параметра работоспособности
достигает предельного уровня при x=9.
Таким образом при проведении технического
обслуживания по состоянию замену системы
надо проводить с периодичностью
= 9. Заметим, что для уровня гарантии
,
при использовании стратегии обслуживания
по гарантированному ресурсу, периодичность
замен равна
=
2.3, что подтверждает высокую эффективность
стратегии технического обслуживания
по состоянию.
Использование метода статистических испытаний
в задачах обеспечения надежности технических систем.