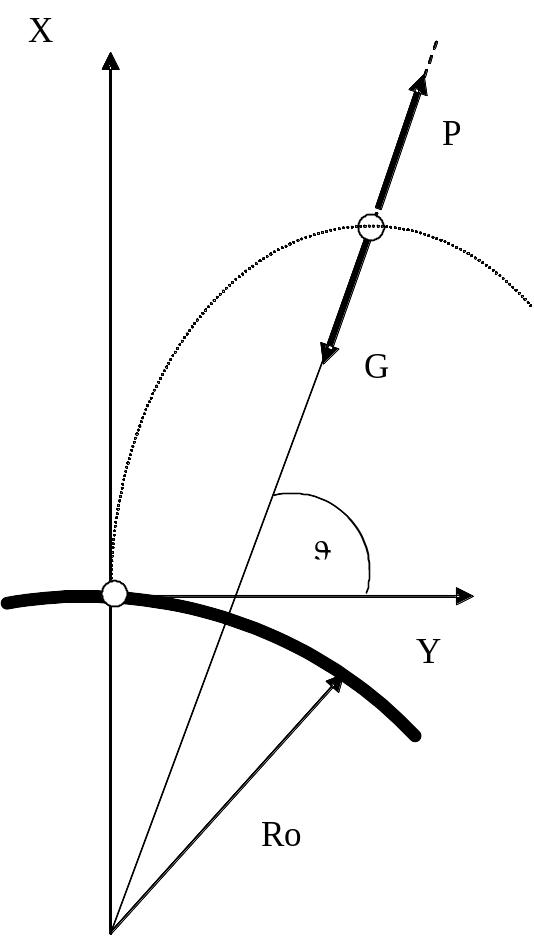
15. Выведение на орбиту

Допущения: – аэродинамические силы отсутствуют;

– гравитационное поле – центральное;

– Земля не вращается.

Модель движения , , ; , .,

где R₀ – радиус сферической Земли;

μ – гравитационная постоянная;

m – масса топлива;

m₀ – масса сухого ЛА;

P – сила тяги двигателя;

J – удельный импульс;

β – секундный расход топлива;

β_m – максимально возможный расход топлива;

h – высота над поверхностью сферической Земли.

g₀ – ускорение силы тяжести на поверхности Земли

В конечный момент времени КА должен быть выведен на круговую орбиту заданного радиуса R* при минимальном расходе топлива.

Найти программу управления углом тангажа, используя необходимые условия оптимального управления.

16. Выведение на орбиту

Допущения: – аэродинамические силы отсутствуют;

– гравитационное поле – центральное;

– Земля не вращается.

Модель движения , , ; , .,

где R₀ – радиус сферической Земли;

μ – гравитационная постоянная;

m – масса топлива;

m₀ – масса сухого ЛА;

P – сила тяги двигателя;

J – удельный импульс;

β – секундный расход топлива;

β_m – максимально возможный расход топлива;

h – высота над поверхностью сферической Земли.

g₀ – ускорение силы тяжести на поверхности

В конечный момент времени КА должен быть выведен на круговую орбиту заданного радиуса R* при минимальном расходе топлива.

Программа управления углом тангажа задана в параметрической форме

.

Следует найти неизвестные параметры , , сведением исходной задачи программирования управления к задаче нелинейного программирования.

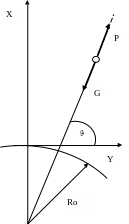
17. Перевод ка в заданное положение на орбите

Космический аппарат орбитальной группировки необходимо перевести в новое место орбитальной структуры. Перевод осуществляется в плоскости опорной круговой орбиты импульсами тяги, прикладываемыми по касательной к орбите. Можно считать, что переходная орбита остается близкой к круговой, а состояние КА можно характеризовать двумя координатами:

x₁ = Δφ – отклонение аргумента широты КА от требуемого при прохождении характерной точки орбиты, например – восходящего узла;

x₂ – скорость дрейфа, численно равная изменению аргумента широты за один драконический период (т.е. между двумя проходами восходящего узла) опорной орбиты.

При импульсной коррекции орбиты математическую модель можно представить в виде

, ,

где N – количество коррекций; – интервал времени (измеряется в оборотах) между коррекциями; u_k – величина k-го импульса скорости дрейфа; μ_k – гауссовская центрированная случайная величина с дисперсией . Статистические характеристики переменных начального состояния заданы.

Цель управления – выполнить терминальные требования

,

при минимальных затратах топлива.

Критерий оптимальности и ограничения аппроксимируем квадратичными функционалами³.

Найти управление , которое обеспечивает минимум энергетических затрат

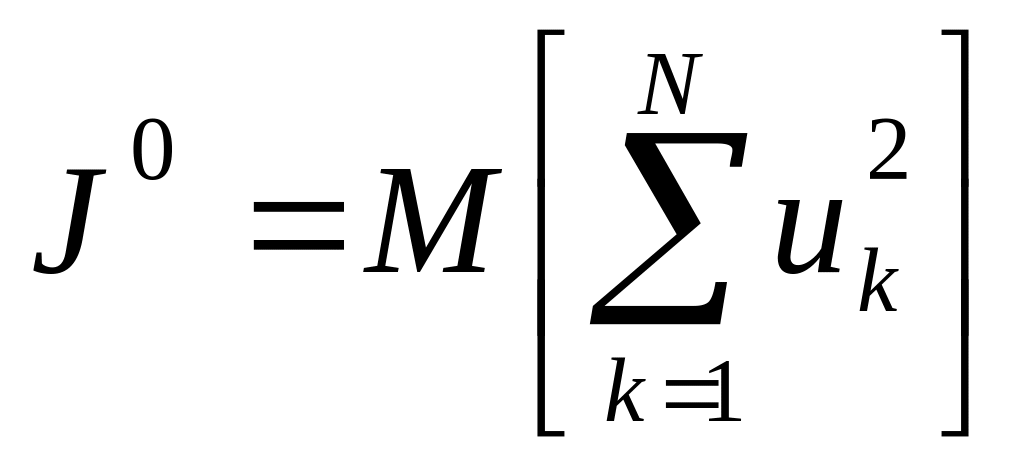при условии ,

где ; 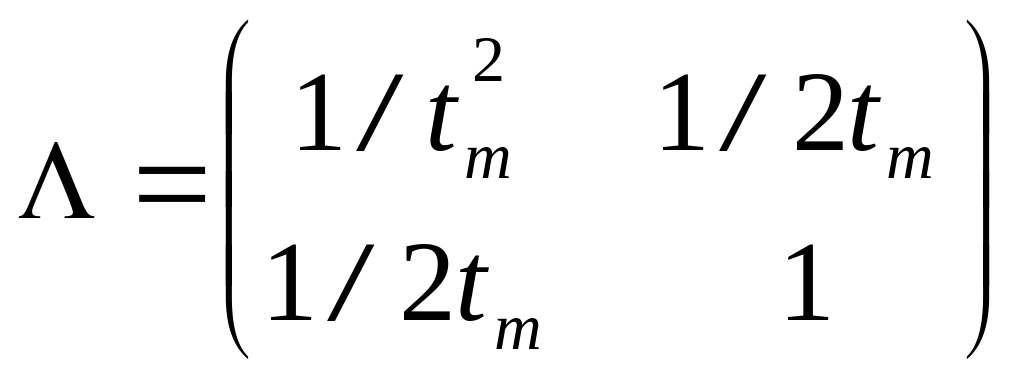, , 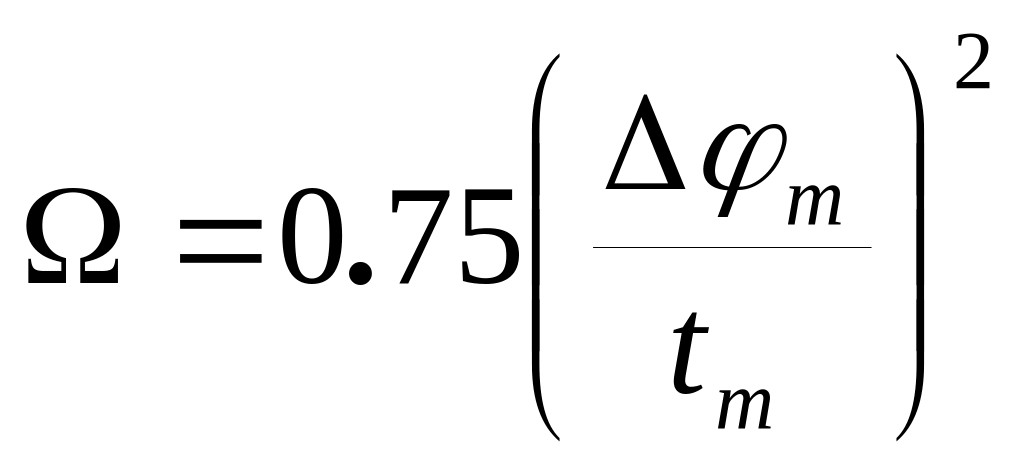– константа, выбираемая так, чтобы терминальные требования выполнялись бы с достаточной вероятностью.

Для решения задачи ввести критерий Лагранжа .

Исследовать зависимости и при различных N.

Длительности пассивных участков могут быть произвольными положительными (заданы).
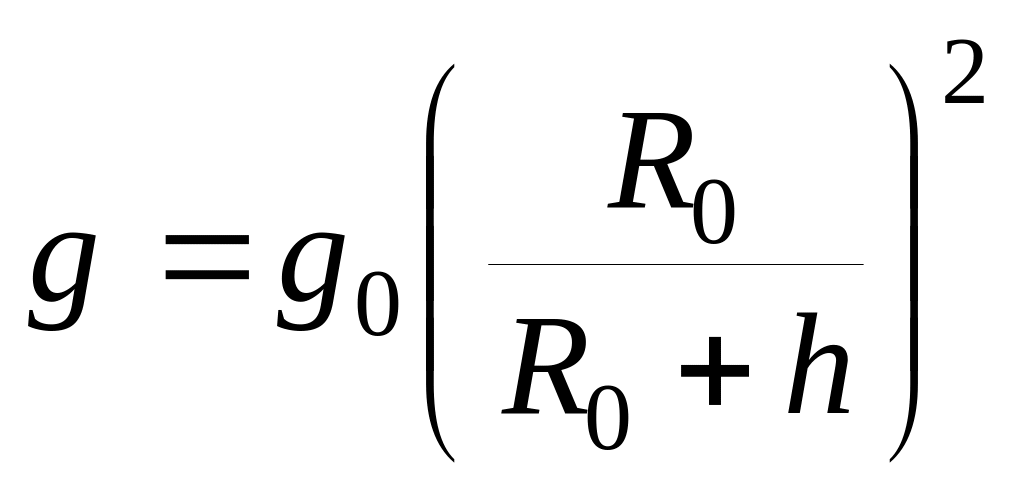