4. Синтез системы стабилизации

Угловое движение ЛА относительно связанной оси Z (тангаж) с достаточной степенью точности можно представить уравнением моментов

,

,

где – угол тангажа;

α – угол атаки;

θ – угол наклона траектории;

δ – угол отклонения руля: ;

– угловая скорость вращения вокруг оси Z;

– момент инерции;

, , – частные производные момента относительно оси Z по соответствующим переменным.

Упрощения: собственное демпфирование мало : .

Угол наклона траектории изменяется очень медленно.

Найти закон управления углом δ, который обеспечит минимальное время регулирования при условиях .

5. Синтез системы стабилизации

Угловое движение ЛА относительно связанной оси Z (тангаж) с достаточной степенью точности можно представить уравнением моментов

,

,

где – угол тангажа;

α – угол атаки;

θ – угол наклона траектории;

δ – угол отклонения руля: ;

– угловая скорость вращения вокруг оси Z;

– момент инерции;

, , – частные производные момента относительно оси Z по соответствующим переменным.

Упрощения: собственное демпфирование мало : . Угол наклона траектории изменяется очень медленно.

Найти закон управления углом δ, который обеспечит минимальное время регулирования при условиях , .

6. Синтез системы стабилизации

Угловое движение ЛА относительно связанной оси Z (тангаж) с достаточной степенью точности можно представить уравнением моментов

,

,

где – угол тангажа;

α – угол атаки;

θ – угол наклона траектории;

δ – угол отклонения руля: ;

– угловая скорость вращения вокруг оси Z;

– момент инерции;

, , – частные производные момента относительно оси Z по соответствующим переменным.

Упрощения: собственное демпфирование мало : . Угол наклона траектории изменяется очень медленно.

Найти закон управления углом δ, который обеспечит минимум критерия

.

7. Программирование оптимального управления ка.

Необходимо перевести КА из одной точки круговой орбиты с радиусом r₀ в другую, считая при этом, что на КА имеется двигательная установка малой тяги, способная создавать управляющее ускорение по нормали к радиус-вектору.

Исходные уравнения движения заданы в полярной системе координат:

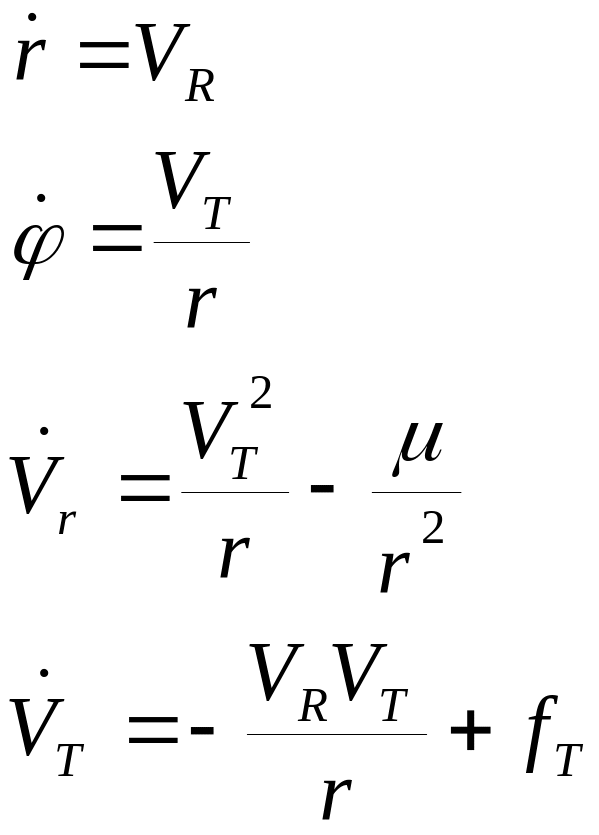
где r – радиус-вектор; φ – угловая полярная координата; V_R, V_T – радиальная и трансверсальная составляющие скорости; μ – гравитационная постоянная Земли: f_T – управляющее ускорение.

Полагая, что в процессе перевода отклонения , , , фазовых координат r, V_R, V_T от соответствующих значений r₀, , V_R=0, на круговой орбите радиуса достаточно малы, линеаризуйте уравнения и приведите модель движения в отклонениях к виду

,

где , u = f_T. Начальное состояние по условию задачи – нулевой вектор.

Терминальное состояние определяется вектором , - заданное угловое расстояние;

Т – длительность процесса перевода подлежит определению.

Оптимальное управление u(t) должно обеспечить выполнение терминальных условий и минимизировать критерий, характеризующий энергетические затраты

.

Терминальные требования аппроксимировать квадратичным штрафом.

Примечание. В уравнениях движения целесообразно перейти к безразмерным переменным с использованием соотношений:

, , , , где .