
- •Магнитное поле в вакууме
- •Взаимодействие проводников с током
- •Индукция магнитного поля.
- •Силовые линии магнитного поля
- •Магнитное поле бесконечно длинного проводника с током
- •Магнитное поле соленоида
- •Сила Лоренца
- •Магнитное поле движущегося заряда
- •Закон Био-Савара-Лапласа
- •3.Магнитного поля кругового тока
Магнитное поле движущегося заряда
Можно
ожидать, что в отличие от статического
электрического поля, обладающего
сферической симметрией, магнитное
поле должно обладать осевой симметрией,
поскольку в окружающем пространстве,
являющемся изотропным, появляется
выделенное направление (направление
вектора скорости
![]() )
)
Рассмотрим магнитное поле, создаваемое в некоторой точке пространства Р точечным зарядом q, движущимся с постоянной скоростью
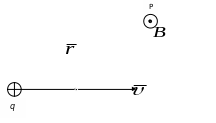
Если t - время, за которое возмущение поля, передающееся со скоростью с достигает точки Р, то из общих соображений
![]()
Вид этой функции f может быть установлен только экспериментально.
При
условии
![]() время запаздывания
время запаздывания
![]() пренебрежительно
мало и
пренебрежительно
мало и
![]()
Опыт даёт, что магнитная индукция поля движущегося точечного заряда:
в
системе «СИ»
![]() т.е. В
~
т.е. В
~![]() (сравним Е
~
)
(сравним Е
~
)
Направление
вектора
определяется правилом буравчика
(правилом правого винта). Поступательное
движение буравчика совпадает с
направлением вектора скорости![]() ,
т.е., с направлением движения положительного
заряда. Вектор магнитной индукции В
в точке
Р
окажется, согласно этому правилу,
направленным "к нам".
,
т.е., с направлением движения положительного
заряда. Вектор магнитной индукции В
в точке
Р
окажется, согласно этому правилу,
направленным "к нам".
 расположен перпендикулярно плоскости,
в которой лежат
расположен перпендикулярно плоскости,
в которой лежат
![]() и
(смотри предыдущий рисунок).
и
(смотри предыдущий рисунок).
Закон Био-Савара-Лапласа
Закон Б-С-Л позволяет определить вектор индукции магнитного поля, создаваемого токами разной формы.
Опыт
показывает, что вектор
пропорционален силе тока, длине
проводника, зависит от формы тока и
расстояния до рассматриваемой точки.
зависимость
от расстояния исследовали для прямого
и кругового токов - Био и Савар. Они
пришли к выводу, что
в данной точке обратно пропорциональна
её расстоянию до тока. Зависимость от
формы тока можно учесть, если, по
предложению математика Лапласа, ввести
понятие элемента
тока
![]() .
Элементом тока называется вектор, равный
по модулю произведению
силы тока на элемент длины проводника
и направленный вдоль тока.
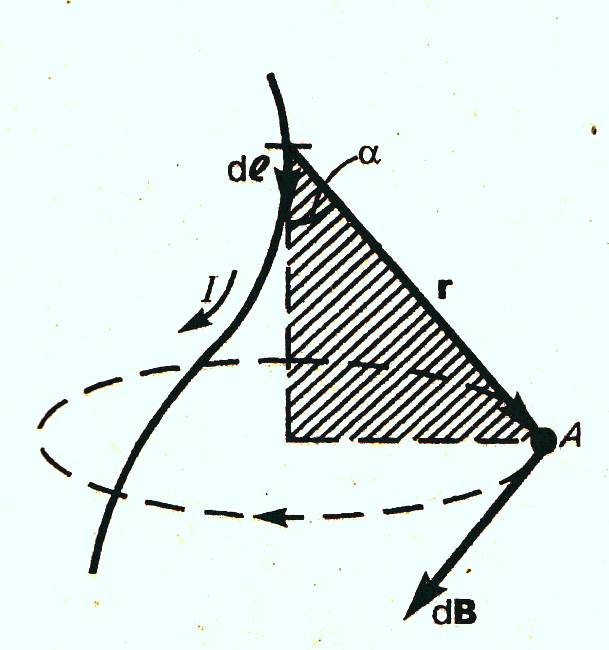
Рассмотрим ток произвольной формы (см.
рисунок). Одна (+) заряженная частица
создаёт в точке А магнитное поле с
вектором
,
направленным к нам от плоскости чертежа
(если точка А лежит в плоскости чертежа).
.
Элементом тока называется вектор, равный
по модулю произведению
силы тока на элемент длины проводника
и направленный вдоль тока.
Рассмотрим ток произвольной формы (см.
рисунок). Одна (+) заряженная частица
создаёт в точке А магнитное поле с
вектором
,
направленным к нам от плоскости чертежа
(если точка А лежит в плоскости чертежа).
![]() ,
где
-
скорость теплового хаотического
движения,
,
где
-
скорость теплового хаотического
движения,
![]() -
дрейфовая скорость упорядоченного
движения электрических зарядов под
действием электрического поля.
-
дрейфовая скорость упорядоченного
движения электрических зарядов под
действием электрического поля.
Заряд
элемента проводника длины dl
, имеющего поперечное сечение S
и плотность носителей в единице объема
n
равен nSdl.
Поскольку среднее значение скорости
теплового движения электронов <
>=0,
то магнитное поле в точке А, создаваемое
элементом длины
dl
( если взять q=e
), так назывемый, элемент
вектора магнитной индукции:
![]() .
.
![]() ,
т.к. ne<
>=
,
т.к. ne<
>=![]() ,
то
,
то
![]() ,
сделаем замену, т.к.
,
сделаем замену, т.к.
![]() ,
поскольку направления
,
поскольку направления
![]() и
совпадают, то
и
совпадают, то
![]() ,
а т.к. Sj=I,
то, окончательно, закон Био-Савара-Лапласа
в векторном виде может быть представлен
следующей формулой:
,
а т.к. Sj=I,
то, окончательно, закон Био-Савара-Лапласа
в векторном виде может быть представлен
следующей формулой:
![]()
В скалярном виде индукция магнитного поля, создаваемая элементом тока (закон Био-Савара-Лапласа) принимает вид:
![]() ,
,
![]() г
где,
r
– радиус-вектор, проведенный из элемента
тока Idl
в
точку А. Направление вектора dB
перпендикулярно
dl
и
r
и
по направлению совпадает с касательной
к линии магнитной индукции и может быть
найдено по правилу правого винта для
тока, протекающего через элемент длины
dl.
г
где,
r
– радиус-вектор, проведенный из элемента
тока Idl
в
точку А. Направление вектора dB
перпендикулярно
dl
и
r
и
по направлению совпадает с касательной
к линии магнитной индукции и может быть
найдено по правилу правого винта для
тока, протекающего через элемент длины
dl.
Используя закон БИО-САВАРА-ЛАПЛАСА можно получить формулы:
1.магнитного
поля прямого тока

![]()
2.магнитного
поля соленоида
![]()
N – число витков катушки соленоида
