Сумы и произведения

Синтаксис: sum(функция, переменная, индекс_начального_члена_ ряда,

индекс_конечного_члена _ряда).

Синтаксис функции произведения аналогичен функции суммы:

product (функция, переменная, индекс_начального_члена_ ряда, индекс_конечного_члена _ряда).

Если конечный член ряда меньше начального, Maxima в ответе возвращает единицу.

Решение алгебраических уравений

Уравнения и системы уравнений решаются в Maxima одной и той же функцией solve. Интерфейс wxMaxima позволяет упростить процедуру использования функции solve: после нажатия на кнопку «Решить» в меню «Уравнения» появится дополнительное окно «Решить», в котором конкретизируется и вид уравнения, и имя переменной, относительно которой нужно решить уравнение.

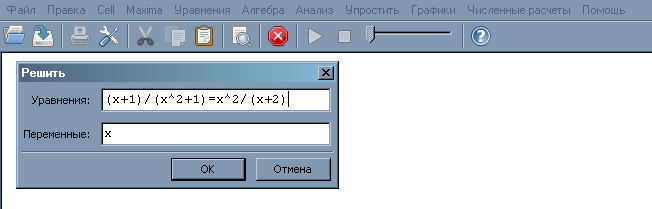
на что получим соответственный результат:

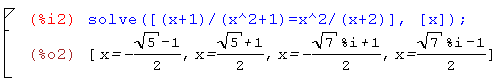
Корни уравнений, как видно, Maxima возвращает в виде списков.

Для записи команды решения системы уравнений для Maxima можно использовать следующий вариант:

solve([уравнение1, уравнение2, …], [переменная1, переменная2, …]),

но можно использовать сокращенный вариант, аналогично варианту для одиночного уравнения.

Пример:

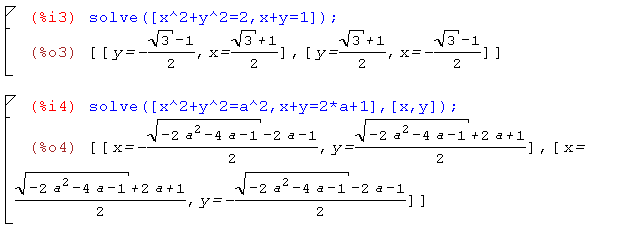
Если же solve не сможет найти точных решений, то она может поступить как функция integrate и вернуть уравнение или систему уравнений в некотором упрощенном виде, а может и самостоятельно попытаться решить систему численно.

Попробуем найти точки пересечения двух кривых второго порядка: гиперболы 4x2 – y2 = 12 с гиперболой xy – x = 2.

Мы получили в качестве решения список, в котором имеются 4 (численных) приближенных решения, два из них – это действительные координаты точек пересечения и два других – комплексные корни, содержащие мнимую единицу %i.

Но если нам все же нужны точные значения корней (в аналитической записи), либо если они не найдены даже в числах, можно попробовать решить уравнения по очереди, выражая одно неизвестное через другое. Для данной пары уравнений решим второе из уравнений eq относительно y, подставим найденное решение в первое уравнение и решим его относительно х.

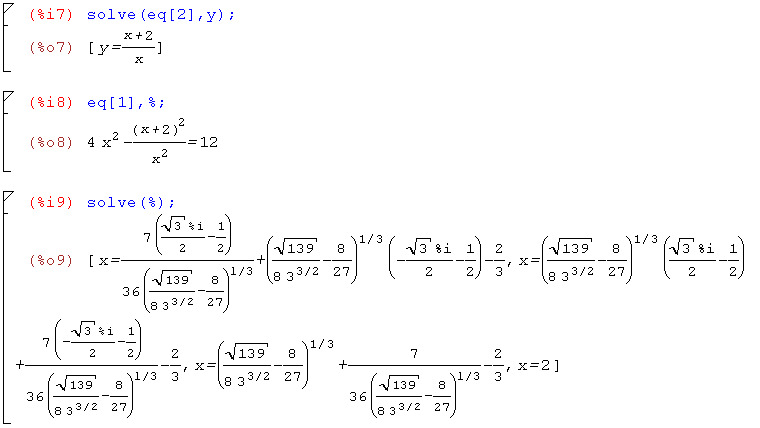
В результате решения получим 4 различных корня, в том числе 2 корня комплексные.

Решение обыкновенных дифференциальных уравнений.

Для решения ОДУ первого порядка применяется функция

ode2 (уравнение. зависимая переменная, независимая переменная). На завершающем этапе начальное условие подставляется функцией ic1.

Пример:

Решение ОДУ 2 порядка.

Первые 2 этапа схожи с предыдущим решением:

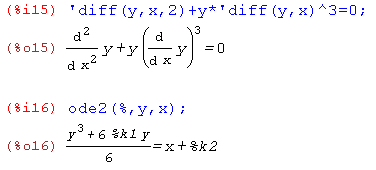
Для подстановки начального условия используем функцию ic2 (начальное условие для ОДУ второго порядка) и сразу упрощаем полученный ответ при помощи функции ratsimp:

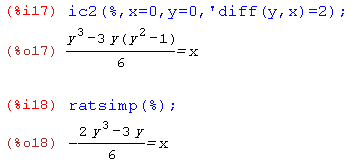
В случае граничной задачи применяется функция bc2 (в качестве параметров указываются значения функции в двух точках)

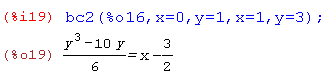
Пример:

решить задачу Коши для дифференциального уравнения второго порядка:

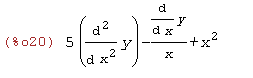
на отрезке [1,3] при начальных условиях y’(1)=1, y(1)=1.

На первом этапе записываем дифференциальное уравнение и решаем его при помощи функции ode2.

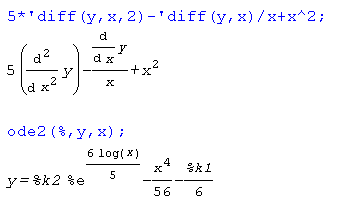
Задаем начальные условия.