Логические конструкции и выражения

В Maxima, в отличие от большинства «традиционных» процедурных и объектных языков программирования, где существует так называемый условный оператор, привычная связка

if условие then выражение1 else выражение2

является не синтаксической конструкцией, а оператором. При выполнении «условия» из двух «выражений» вычисляется только первое и возвращается как результат оператора; в противном случае выполняется только второе и оно же является значением всего выражения «if-then-else». Часть конструкции - «выражение2», как и в большинстве языков программирования, опциональна. Если ее нет, а условие все-таки не выполнилось, результат оператора if будет равен false.

Пример:

Немного о самих условиях, которые могут проверяться оператором if. Условия >, <, >=, <= записываются и расшифровываются традиционно, так же как и логические операторы and, or, not. В то же время равенства в Maxima есть двух видов: синтаксические и логические. Знаком «=» обозначается как раз первое, а второе вычисляется с помощью функции equal().

Пример:

(дополнительно используется предикат «is», который проверяет на истинность свой аргумент)

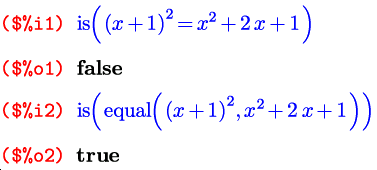
Неравенств, соответственно, также существует два вида. Синтаксическое неравенство обозначается символом логическое неравенство обозначено через notequal().

Символьная матеатика

Одним из важнейших достоинств, и основной задачей систем компьютерной алгебры является возможность осуществления различных символьных операций, результат которых представляется в виде выражения или формулы. К основным символьным операциям относятся дифференцирование, интегрирование, разложение в ряды, нахождение пределов функций, решение уравнений, в том числе дифференциальных, алгебраические преобразования.

Дифференцирование.

Функция diff(); позволяет найти производные, как первого, так и более высоких порядков. При наличии у функции нескольких переменных можно найти частную производную по одной из них.

Синтаксис: diff(функция, переменная, порядок производной);

Пример:

найти первую производную функции

Для вычисления производной вводится команда: diff(y(x),x,1); или diff(y(x),x);. В случае первой производной ее порядок можно не указывать.

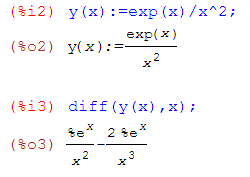
При вычислении кратных производных по нескольким переменным после указания функции перечисляются переменные дифференцирования с указанием соответствующих кратностей, например:

diff(x^8*y^5, x, 4, y, 2); — дифференцирует функцию x⁸y⁵ по переменной х четыре раза и по переменной у два раза

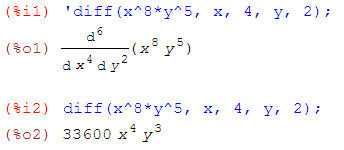
Если функция diff() содержит только один аргумент, то функция diff(выражение); вычисляет не производную записанного выражения, а полный дифференциал этого выражения. Другими словами, запись diff(f, x); равнозначна математическому обозначению df/dx, а diff(f) — df.

Кроме того, функция diff() используется еще и для обозначения производных в дифференциальных уравнениях.

Интегрирование

Для нахождения неопределенного интеграла в качестве аргументов указывается функция и переменная интегрирования.

Синтаксис: integrate (функция, переменная);

Пример:

вычислить интеграл от функции х2+5х+3 по переменной х.

При нахождении значения определенного интеграла помимо рассмотренных параметров указываются пределы интегрирования. В качестве пределов интегрирования могут фигурировать бесконечность (inf) и минус бесконечность (minf).

Синтаксис: integrate(функция, переменная, нижний предел, верхний предел);

Пример:

вычислить интеграл функции sin(x) по переменной х на отрезке от 0 до pi

В случае если интеграл расходится, Maxima выдает сообщение «Integral is divergent»

В некоторых случаях Maxima может попросить доопределить некоторую переменную, как в случае вычисления определенного интеграла, значение которого зависит от знака параметра а, являющегося верхним пределом, или интегрирования функции.

В следующем примере подынтегральное выражение не зависит от знака параметра a, но значение интеграла — зависит, так как параметр а может быть записан или как верхний предел или как нижний предел.

На вопрос Maxima «Is a positive, negative, or zero?» мы ответили р (positive) и получили положительное значение. В случае отрицательного знака у параметра а значение интеграла (%о14) будет отрицательное, а численное значение интеграла по модулю будет тем же.

В следующем примере прежде чем записать ответ Maxima уточнила, не является ли значение n+1 равным нулю: «Is n+1 zero or nonzero?», после получения положительного ответа nonzero Maxima, наконец, записала численное значение интеграла