4.7. Закон Джоуля - Ленца

Электрический ток, как об этом свидетельствует закон Ома, существу­ет в проводнике благодаря действию на носители тока электростатиче­ских и сторонних сил. Под действием этих сил подвижные заряженные частицы в проводнике ускоряются. Однако, сталкиваясь с малоподвиж­ными частицами среды, они отдают им часть своей кинетической энер­гии. Так, энергия носителей тока переходит во внутреннюю энергию проводника. При этом проводник нагревается и отдает тепло в окружа­ющую среду.

Если ток, текущий в проводнике, не очень быстро изменяется с те­чением времени, то через любое сечение этого проводника за время dt будет перенесен один и тот же заряд

dQ = Idt.

Работа при переносе заряда dQ на некотором участке проводника равна произведению этого заряда на падение напряжения на данном участке:

dA = dQU = IUdt.

Согласно закону сохранения энергии работа dA сил, действующих на носители тока, равна приращению dW их кинетической энергии, которое затем в виде тепла передается веществу проводника:

dW = dA .

Таким образом, в проводнике с током за время dt выделяется тепловая энергия

dW = IUdt. (4.27)

Скорость преобразования энергии из одного вида в другой или ско­рость передачи энергии от одного тела к другому называют мощностью Р. По определению

P(t) = dW /dt,

В рассматриваемом случае мощность Р есть количество тепла, которое выделяется за единицу времени в проводнике при прохождении по нему электрического тока, и называется мощностью тока. Теперь формулу (4.27) можно записать так:

| dW = P(t) dt, (4.28)

(4.29)

Тепло W, которое выделяется в проводнике с током за время от момента времени t₁ до момента t₂, равно интегралу от выражения (4.28):

W= P(t)dt (4.30)

Формулы (4.27) - (4.30) выражают собой закон Джоуля - Ленца. Еди­ница мощности в СИ - ватт ( Вт ): [Р] = Вт = А*В.

W = - закон Джоуля–Ленца.

Глава 4

ЭЛЕКТРИЧЕСКИЙ ТОК

(продолжение)

4.8. Сила тока — поток плотности тока

Рассмотрим теперь общий случай упорядоченного движения заряжен­ных частиц в проводящей среде. Носители тока являются микроско­пическими частицами, совершающими беспорядочное тепловое движе­ние. При этом каждая частица в данное мгновение имеет свою скорость. Пусть в некотором физически бесконечно малом объеме dV проводни­ка содержится dN носителей тока. Средней скоростью упорядоченного движения этих частиц называется вектор и, определяемый формулой

dN

dV

где щ - скорость одной из частиц, содержащихся в объеме dV, г - номер частицы. Вектор и можно определить таким образом для любой точки пространства внутри проводника, т.е. объем dV молено располо­жить в любом месте проводника. Иначе говоря, вектор средней скорости есть функция точки пространства. Кроме этого, средняя скорость может изменяться со временем: й = u(t, r). Когда частицы движутся совершен­но беспорядочно, их средняя скорость равна нулю. Если же заряженные частицы движутся преимущественно в одном направлении, то и ф 0, т.е. по проводнику идет электрический ток.

Плотностью электрического тока называют вектор

dV

где qi - заряд частицы под номером г, заключенной в объеме dV. Плот­ность тока в различных малых объемах dV проводника может принимать различные значения и может изменяться с течением времени:

J=J(t,r). , (4.зз)

В том случае, когда все носители тока имеют одинаковые заряды: Qi — формула (4.32) принимает вид

q п г (4.34)

концентрация носителей тока. Объемная плотность q свободных заря­дов связана с концентрацией носителей тока соотношением

Поэтому формулу (4.34) можно записать так:

(4.35)

Пусть в пространстве, заполненном проводящей средой, по которой те­чет электрический ток, задано векторное поле j — j(t, r), описывающее этот ток. Линиями тока называются линии, касательные к которым в каждой точке пространства совпадают по направлению с вектором плот­ности тока. Построим внутри проводника с током произвольный замкну­тый контур С. Проведем через каждую точку этого контура линию тока. Образованная этими линиями поверхность называется трубкой линий то­ка, а объем внутри этой поверхности - трубкой тока (рис. 4.8).

Рис. 4-9. К определению силы тока

Произведем сечение "узкой" трубки тока некоторой поверхностью S (рис. 4.9). Пусть dS есть площадь сечения, an- единичный вектор, перпендикулярный к поверхности S. Выясним физический смысл потока

вектора плотности тока через элемент поверхности

Рис. 4-8- Линии тока и трубка тока

dl = jdS ,

dldt = \g\u cos в dSdt,

где dS = ndS - векторный элемент

где в - угол между вектором плотности тока и нормалью к поверхности, dt - произвольный интервал времени. Построим еще одно сечение dS₀ трубки тока, которое находится на расстоянии и dt от сечения dS. Объем части трубки тока между этими сечениями, т.е. объем цилиндра, равен и dt cos в dS. Предположим, что электрический ток создается движением положительных зарядов. Эти заряды сначала протекают через сечение dS₀, а затем - через dS. Произведение и dt есть среднее расстояние, которое преодолевает носитель тока за время dt, двигаясь вдоль линии тока. Поэтому все носители тока, которые имелись внутри трубки тока между сечениями dS₀ и dS в некоторый момент времени, спустя время dt окажутся за сечением dS. При этом они перенесут через сечение dS свой электрический заряд, который равен произведению плотности заряда q на объем той части трубки тока, где находились эти частицы. Таким образом, выражение (4.37) есть электрический заряд dQ, протекающий за время dt через элемент поверхности площадью dS:

dQ = dIdt.

Отношение заряда, протекающего через некоторую поверхность, ко вре­мени протекания есть сила тока. Согласно этому определению величина dl в формулах (4.36) и (4.37) есть сила тока, протекающего через элемент поверхности dS:

di=4.

dt

Заряд, протекающий за некоторое время через поверхность S, равен сумме зарядов, протекающих за это время через различные элементы поверхности. Поэтому сила тока I, протекающего через поверхность S, будет равна сумме сил токов dl через элементы этой поверхности, т.е. будет равна потоку вектора плотности тока:

(4.38)

По определению заряд dQ, протекающий через поверхность S за время dt равен произведению силы тока на это время:

dQ = Idt.

(4.39)

Следует заметить, что величина (4.38) является алгебраической. Знак силы тока / зависит от выбора направления вектора ft нормали к по­верхности. Если / < 0, то это означает, что в направлении нормали переносится отрицательный заряд dQ или положительный заряд \dQ\ переносится в противоположном направлении.

Задача. Цилиндр радиуса а вращается вокруг своей оси с угло­вой скоростью ш. Цилиндр заряжен равномерно по объему. Плотность заряда равна д. Найти вектор плотности конвекционного тока.

4.9. Уравнение непрерывности

Когда заряженные частицы совершают направленное движение, их распределение в пространстве может изменяться с течением времени, т.е. объемная плотность зарядов в общем случае зависит не только от координат точки пространства, но и от времени:

q = g(t, i*). (4.40)

Выведем соотношение, связывающее функции (4.33) и (4.40). Для этого рассмотрим произвольный объем V, ограниченный замкнутой поверхно­стью S- Согласно определению объемной плотности заряда интеграл

(4.41)

Q(t) = J Q{t,r)dV

есть электрический заряд, распределенный по объему V, в момент вре­мени t. Этот заряд может изменяться с течением времени, если через поверхность S протекает электрический ток. Сила тока /, протекаю­щего через поверхность S в направлении внешней нормали, есть поток вектора плотности тока:

то I(t) = j(t, r)dS .втос; (4.42)

Пусть за время dt заряд в объеме V изменился на величину dQ. Этот заряд принадлежит тем носителям тока, которые пересекли поверхность 5 за это время. По определению сила тока / есть отношение заряда, протекающего через поверхность S, ко времени dt. Предположим, что сила тока / есть положительная величина. Это означает, что положи­тельный заряд вытекает из объема V или отрицательный заряд втекает в этот объем. В таком случае заряд Q в объеме V уменьшается, а его приращение dQ будет отрицательным. Поэтому справедливо равенство

которое выражает собой закон сохранения заряда.

Подставим интегралы (4.41) и (4.42) в равенство (4.43):

(t,r)dV = -

При помощи теоремы Остроградского - Гаусса заменим поверхностный интеграл в правой части этого равенства объемным интегралом от ди­вергенции вектора j плотности тока. После несложных преобразований придем к уравнению

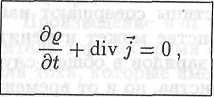
которое называют уравнением непрерывности, или уравнением нераз­рывности.

Рассмотрим два частных случая. Для системы неподвижных зарядов объемная плотность не зависит от времени: д — д{г), а плотность тока равна нулю: j = 0. В этом случае уравнение непрерывности обращается в тождество. Постоянный электрический ток характеризуется не зави­сящими от времени плотностью заряда д = д(г) и вектором плотности тока j = j(r). При этом уравнение непрерывности принимает вид

div j = 0 .