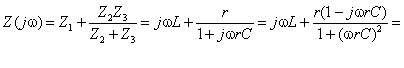1.3. Резонансные режимы двухполюсников с потерями

 

Двухполюсник, включающий полный набор элементов r, L и C, при питании от источника синусоидального тока будет частично потреблять энергию источника в резистивных элементах цепи (активная мощность P>0), а частично участвовать в обмене энергией с источником, периодически запасая ее в реактивных элементах в виде энергии электрического и магнитного поля. Реактивная мощность Q, характеризующая процесс обмена реактивной энергией, в общем случае определяется разностью суммарных реактивных мощностей, запасенных в индуктивностях, и суммарных реактивных мощностей, запасенных в емкостях:

(1.6)

Знак минус в выражении (1.6) означает, что реактивные элементы разных типов обмениваются энергией не только с источником, но и между собой; при этом энергия электрического поля переходит в энергию магнитного поля и наоборот.

На некоторых частотах, которые называются резонансными, суммарная энергия, запасенная в индуктивных элементах , полностью компенсируется энергией, запасенной в емкостных элементах . Тогда суммарная реактивная мощность становится равной нулю (Q = 0), и это условие можно считать одним из определений резонансного состояния цепи. На основе этого вывода следуют ряд положений, каждое из которых можно также считать определением или признаком резонанса:

1. Полная мощность S = P + jQ, потребляемая двухполюсником, целиком определяется активной мощностью P:

S = P

Q = 0

(1.7)

2. Коэффициент мощности становится равным единице, а сам аргумент нулю: cosφ = P/S = 1, φ = 0;

3. Этот же аргумент φ определяет угол сдвига фаз между током и напряжением. Следовательно, на резонансной частоте ток и напряжение на входных зажимах двухполюсника совпадают по фазе: ;

 

4. Угол сдвига фаз φ совпадает по величине с аргументом функции входного сопротивления , который вычисляется по формуле

φ = arctg (X/R)

Если φ = 0, а R не равняется нулю и имеет конечное значение, то мнимая часть функции входного сопротивления должна обращаться в ноль:

X = Jm(Z) = 0

(1.8)

Этим выражением пользуются для определения точек резонанса напряжений, т.е. нулевых резонансных частот.

5. Аналогичные рассуждения можно привести и для функции входной проводимости двухполюсника, которая определяется как величина, обратная входному сопротивлению (см. (1.2)):

Если φ = 0, а G не равняется нулю и имеет конечное значение, то

мнимая часть функции входной проводимости должна обращаться в ноль:

B = Jm(Y) = 0

(1.9)

Этим выражением пользуются для определения точек резонанса токов, т.е. полюсных резонансных частот.

В двухполюсниках с потерями число резонансных частот зависит не только от общего числа реактивных элементов цепи, но и от численных значений параметров r, L и C. Это положение приводит к необходимости дополнительного исследования тех выражений резонансных частот, которые определяются в результате использования условий (1.8) и (1.9). Кроме того, перед решением задачи необходимо установить какие резонансные режимы могут иметь место в рассматриваемой цепи. Для этого рекомендуется рассмотреть две предельные задачи: первая из них получается из исходной цепи путем замены всех резистивных элементов на ноль (r = 0), вторая задача предполагает замену всех резистивных элементов на бесконечность (r = ∞), что означает разрыв ветвей, содержащих резистивные элементы. Обе предельные задачи преобразуют исходную цепь к чисто реактивной, для которой легко просматриваются возможные резонансные режимы (см. выше раздел 1.2).

 

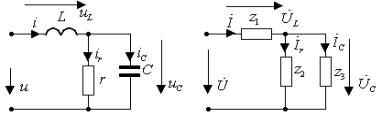
Пример 1.4. Исследовать резонансные режимы для цепи, изображенной на рис.1.8а.

Анализ цепи начинаем с двух предельных схем замещения рис.1.9а,б, которые будут иметь место, если r = ∞ (режим холостого хода х.х.) и r = 0 (режим короткого замыкания к.з.).

а) б)

Рис. 1.8. Схема двухполюсника с потерями:

а)исходная схема; б)комплексная схема

 

В схеме рис.1.9a реактивные элементы L и C соединены последовательно, и в этой цепи возможен резонанс напряжений. В цепи рис.1.9б элемент С замкнут накоротко, и входное сопротивление двухполюсника определяется только индуктивностью L; следовательно в такой цепи резонанса быть не может.

а) б)

Рис. 1.9. Предельные схемы замещения двухполюсника: а)r→∞;б) r→0

 

Итак, возвращаясь к исходной цепи рис.1.8а, делаем вывод о возможном резонансе напряжений в заданной цепи при определенном соотношении параметров r, L и C.

Переходим к анализу комплексной схемы замещения исходной цепи рис.1.8б, где ; ; . Находим входное сопротивление и приводим его к алгебраической форме записи, освобождаясь от мнимости в знаменателе путем умножения числителя и знаменателя второго слагаемого на комплексно-сопряженное выражение. Произведенные действия позволяют выделить в общем виде мнимую часть входного сопротивления

Используя условие резонанса напряжений (1.8), приравниваем мнимую часть полученного выражения к нулю

Достаточно приравнять к нулю числитель и решить полученное уравнение относительно частоты ω.

Решение включает два корня: и .

Первый корень характеризует поведение цепи на постоянном токе, когда не происходит обмена реактивной мощности между индуктивностью L и емкостью C, а вся энергия источника тратится в резистивном элементе r: . Выражение для второго корня можно преобразовать к виду, близкому к известной формуле Томсона, если вынести за знак квадратного корня выражение :

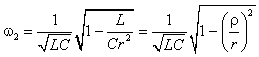
(1.10)

где в конечное выражение введена величина , которая называется волновым сопротивлением последовательного колебательного контура. Полученное выражение (1.10) показывает, что при выполнении условия r > ρ в цепи будет иметь место резонанс напряжений. При этом входное сопротивление двухполюсника будет определяться только его вещественной частью:

Если численные параметры цепи такие, что выполняется обратное условие r < ρ, то резонанса в цепи не будет.

Векторная диаграмма токов и напряжений, соответствующая резонансному режиму, показана на рис.1.10.

 

 

 

Рис. 1.10. Векторная диаграмма токов и напряжений

 

При построении векторной диаграммы учтено, что ток и напряжение совпадают по фазе, т.е. . Кроме того должно выполняться равенство , что характеризует баланс реактивных мощностей.

Задача решена.