4. Задачи для самостоятельного решения

Приложение 1. Задачи к первому разделу пособия.

 

Задание 1. Исследование частотных характеристик.

Для схем, изображенных на рис.1п, найти:

а. Указанную в таблице 1п комплексную передаточную функцию H(jω), для чего к зажимам 1-1 присоединить источник, а к зажимам 2-2^’ сопротивление нагрузки Z_н, которое носит резистивный характер.

б. Выделить из комплексной передаточной функции АЧХ — H(ω) и ФЧХ - θ(ω). Записать найденные выражения в зависимости от относи-тельной частоты Ω, где Ω = ωL/R или Ω = ωRC.

в. Рассчитать найденные частотные характеристики на десяти часто-

тах, включая 0 и ∞. Построить графики АЧХ и ФЧХ в зависимости от относительной частоты.

г. Используя заданные параметры цепи R, L, C, сделать переход к угловой частоте ω [рад./с] и к реальной частоте f [Гц]. Изобразить ось реальных частот на графиках АЧХ и ФЧХ.

д. Сделать вывод о способности четырехполюсника пропускать сигналы разных частот.

а) б) в) г)

д) е) ж) з)

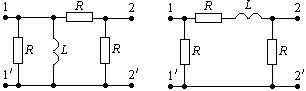
и) к) л) м)

н) о) п) р)

с) т)

Рис. 1п.

Таблица 1п

 

Вар.	Схема	L, мГн	C, мкФ	R,Ом	Zн, Ом	Определить H(jω)
1	а	10	-	4000	2R	Zвх.	Ki	Zп
2	б	200	-	10	4R	Ku	Yвх.	Yп
3	в	-	2.0	300	3R	Yвх.	Ku	Yп
4	г	-	0.5	1000	R	Zп	Ki	Zвх.
5	д	-	0.1	500	R	Ki	Zп	Zвх.
6	е	-	0.2	300	2R	Zп	Zвх.	Ki
7	ж	-	1.5	50	2R	Zвх.	Ki	Zп
8	з	-	2.5	600	R	Ki	Zп	Zвх.
9	и	100	-	400	4R	Zп	Zвх.	Ki
10	к	150	-	200	R	Zвх.	Ki	Zп
11	п	20	-	3000	R	Ki	Zп	Zвх.
12	о	400	-	20	3R	Ku	Yвх.	Yп
13	м	40	-	400	R	Zп	Ki	Zвх.
14	л	-	1.5	2000	2R	Zвх.	Zп	Ki
15	н	-	0.2	200	3R	Yп	Ku	Yвх.
16	р	-	0.1	400	R	Ki	Zвх.	Zп
17	т	-	3.0	60	2R	Zп	Ki	Zвх.
18	с	20	-	500	2R	Zвх.	Zп	Ki
19	и	200	-	250	R	Ki	Zп	Zвх.
20	к	-	1.5	400	3R	Zп	Zвх.	Ki
21	а	30	-	2500	R	Ki	Zп	Zвх.
22	б	300	-	350	5R	Ku	Yп	Yвх.
23	п	60	-	600	2R	Zвх.	Ki	Zп
24	г	-	4.5	4000	R	Yп	Ku	Yвх.
25	д	-	0.5	300	R	Zп	Zвх.	Ki
26	е	-	0.2	500	R	Ku	Yп	Yвх.
27	ж	-	4.0	80	3R	Ki	Zп	Zвх.
28	с	60	-	150	2R	Zвх.	Ki	Zп
29	м	150	-	800	4R	Zп	Zвх.	Ki
30	л	-	3.5	200	3R	Yвх.	Yп	Ku

 

Задача 2п. Найти А - параметры четырехполюсников, схемы которых представлены на рис.1п (без подключения сопротивления нагрузки). Ис-

пользуя выражения (1.27) и (1.28),найти коэффициенты передачи напряжения и тока с учетом сопротивления нагрузки Z_н = 2R .

Задача 3п. Найти резонансные частоты для двухполюсников с потерями, схемы которых изображены на рис.2п. Указать, какие условия должны соблюдаться, чтобы резонанс имел место. Построить векторную диаграмму токов и напряжений для резонансного состояния цепи.

а) б) в)

 

г) д) е) ж)

Рис. 2п.

Задача 4п. Найти резонансные частоты для схем реактивных двухполюсников, представленных на рис.3п.

а. Построить качественно АЧХ функции входного сопротивления.

б. Построить качественно АЧХ функции входной проводимости.

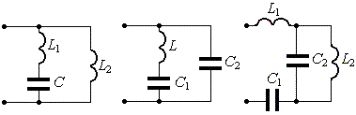
а) б) в) г) д) е)

Рис. 3п.

Приложение 2. Задачи ко второму разделу пособия.

 

Задание 2. Несинусоидальные периодические токи.

На входе цепи рис.1п действует источник несинусоидального периодического сигнала - тока или напряжения, форма которого задана в таблице 2.Здесь под V следует понимать либо максимальное значение тока V = 10 А, либо максимальное значение напряжения V = 100 В. Характер воздействия определен выбором варианта задания и указан в таблице 2п: i₁(t) или u₁(t).

Во всех вариантах задания считать, что на основной (первой) гармонике сигнала выполняются численные равенства x_С1 = 2R; x_L1 = 0,5R.

Для сигналов прямоугольной формы 5 и 6 (табл.2) принять отношение

длительности сигнала к периоду T равным любому из значений:

τ/T = 0,10;0,15;0,20;0,25.

Параметры цепи выбираются по номеру варианта из таблицы 1п.

Требуется исследовать процесс прохождения сигнала в цепи, для чего

следует:

а. В соответствии с указанным вариантом подсоединить к входным за-

жимам источник сигнала, а к выходным - сопротивление нагрузки.

б. Ограничиваясь первыми пятью членами ряда Фурье, рассчитать амплитудный и фазовый спектр входного сигнала.

в. Найти АЧХ и ФЧХ исследуемой цепи. Используя указанные выше соотношения резистивных и реактивных параметров, записать выражения для АЧХ и ФЧХ как функции целочисленной переменной k. Если эти характеристики уже были найдены при выполнении Задания 1, то перейти в них от относительной переменной к целочисленной - k. Найти численные значения характеристик для выбранных значений k.

г. Рассчитать амплитудный и фазовый спектр выходного сигнала. Численные значения, определенные в пунктах б, в и г свести в таблицу.

д. На одном графике построить и сравнить линейчатые спектры входного и выходного сигнала.

Построить графики АЧХ и ФЧХ исследуемой цепи в зависимости от целочисленной переменной k.

е. Записать выражение выходного сигнала как сумму гармоник и пост-

роить график этой функции. Сравнить этот график с входным сигналом.

ж. Определить интегральные характеристики выходного сигнала:

1. Действующее значение;

2. Коэффициенты амплитуды, формы, нелинейных искажений.

 

 

Таблица 2п

Вар	Схема	Входной сигнал			Передаточная характеристика H(jω)			Выходной сигнал
		вид	характер					i(t)			u(t)
1	а	1	i1	-	Zвх.	Ki	Zп	-	i2	-	u1	-	u2
2	б	2	-	u1	Ku	Yвх.	Yп	-	i1	i2	u2	-	-
3	в	3	-	u1	Yвх.	Ku	Yп	i1	-	i2	-	u2	-
4	г	4	i1	-	Zп	Ki	Zвх.	-	i2	-	u2	-	u1
5	д	5	i1	-	Ki	Zп	Zвх.	i2	-	-	-	u2	u1
6	е	6	i1	-	Zп	Zвх.	Ki	-	-	i2	u2	u1	-
7	ж	7	i1	-	Zвх.	Ki	Zп	-	i2	-	u1	-	u2
8	з	8	i1	-	Ki	Zп	Zвх.	i2	-	-	-	u2	u1
9	и	1	i1	-	Zп	Zвх.	Ki	-	-	i2	u2	u1	-
10	к	2	i1	-	Zвх.	Ki	Zп	-	i2	-	u1	-	u2
11	п	3	i1	-	Ki	Zп	Zвх.	i2	-	-	-	u2	u1
12	о	4	-	u1	Ku	Yвх.	Zп	-	i1	i2	u2	-	-
13	м	5	i1	-	Zп	Ki	Zвх.	-	i2	-	u2	-	u1
14	л	6	i1	-	Zвх.	Zп	Ki	-	-	i2	u1	u2	-
15	н	7	-	u1	YП	Ku	Yвх.	i2	-	i1	-	u2	-
16	р	8	i1	-	Ki	Zвх.	Zп	i2	-	-	-	u1	u2
17	т	1	i1	-	Zп	Ki	Zвх.	-	i2	-	u2	-	u1
18	с	2	i1	-	Zвх.	Zп	Ki	-	-	i2	u1-	u2	-
19	и	3	i1	-	Ki	Zп	Zвх.	i2	-	-	-	u2	u1
20	к	4	i1	-	Zп	Zвх.	Ki	-	-	i2	u2	-	-
21	а	5	i1	-	Ki	Zп	Zвх.	i2	-	-	-	u2	u1
22	б	6	-	u1	Ku	Yп	Yвх.	-	i2	i1	u2	-	-
23	п	7	i1	-	Zвх.	Ki	Zп	-	i2	-	u1	-	u2
24	г	8	-	u1	YП	Ku	Yвх.	i2	-	i1	-	u2	-
25	д	1	i1	-	Zп	Zвх.	Ki	-	-	i2	u2	u1	-
26	е	2	-	u1	Ku	Yп	Yвх.	-	i2	i1	u2	-	-
27	ж	3	i1	-	Ki	Zп	Zвх.	i2	-	-	-	u2	u1
28	с	4	i1	-	Zвх.	Ki	Zп	-	i2	-	u1	-	u2
29	м	5	i1	-	Zп	Zвх.	Ki	-	-	i2	u2	u1	-
30	л	6	-	u1	Yвх.	Yп	Ku	i1	i2	-	-	-	u2

Приложение 3. Задачи к третьему разделу пособия.

 

Переходные процессы в линейных цепях.

 

Задание 3. Исследовать переходный процесс в цепи первого порядка

(рис.4п; а - р) после коммутации (ключ S замыкается или размыкается).

В цепи действует либо постоянный источник напряжения E, либо постоянный источник тока J. Параметры цепи указаны в таблице 3п.

Определить закон изменения во времени указанной в таблице 4п величины (тока или напряжения).

Решить задачу классическим и операторным методом. Сравнить результаты и построить график искомой функции.

а) б) в) г)

 

д) е) ж) з)

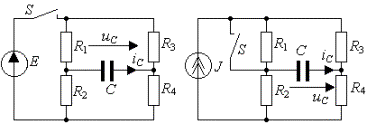
и) к) л) м)

н) о) п) р)

Рис. 4п.

Таблица 3п

Вар.	Схе ма	E,В	J,А	L, мГн	C, мкФ	R1, Ом	R2, Ом	R3, Ом	R4, Ом	Опреде лить	Ключ S
1	а	120	-	1	-	20	20	40	20	uL	зам
2	б	-	2	-	10	40	20	10	30	uC	разм
3	в	100	-	1	-	10	10	25	25	iL	зам
4	г	-	4	2	-	6	6	3	6	i2	разм
5	д	150	-	-	10	50	50	25	25	ic	зам
6	е	-	6	2	-	3	3	3	3	i1	разм
7	ж	120	-	-	5	40	20	20	40	uC	зам
8	з	-	8	1	-	2	4	4	2	uL	разм
9	и	50	-	-	5	20	30	35	15	iC	зам
10	к	-	10	-	5	10	30	35	5	uC	разм
11	л	80	-	10	-	20	60	60	40	u3	зам
12	м	-	12	-	5	12	3	6	3	i4	разм
13	н	100	-	10	-	40	40	20	40	uL	зам
14	о	-	2	-	2	2	4	4	3	i1	разм
15	п	160	-	-	10	20	60	50	30	u4	зам
16	р	-	4	1	-	1	3	4	2	i4	разм
17	а	50	-	10	-	10	40	100	100	i1	разм
18	б	-	6	-	1	20	10	5	15	i1	зам
19	в	60	-	20	-	5	5	15	15	u2	разм
20	г	-	8	10	-	8	8	4	12	uL	зам
21	д	80	-	-	1	20	20	10	10	i3	разм
22	е	-	10	10	-	2	2	4	4	uL	зам
23	ж	100	-	-	2	20	40	45	15	iC	разм
24	з	-	2	2	-	4	2	1	5	iL	зам
25	и	120	-	-	5	40	10	30	30	uC	разм
26	к	-	4	-	10	4	6	8	2	iC	зам
27	л	150	-	8	-	50	50	60	40	i1	разм
28	м	-	6	-	8	12	6	3	3	uC	зам
29	н	180	-	8	-	20	20	40	40	u2	разм
30	о	-	8	-	10	4	8	8	16	iC	зам

 

Задание 4. Исследовать переходный процесс в цепи второго порядка (рис.5п; а - р) после коммутации (ключ S замыкается или размыкается).

В цепи действует либо постоянный источник напряжения E, либо постоянный истоник тока J. Параметры цепи указаны в таблице 4п.

Определить закон изменения во времени указанной в таблице 4п величины (тока или напряжения).

Решить задачу классическим и операторным методом. Сравнить результаты и построить график искомой функции.

 

а) б) в) г) д) е) ж) з)

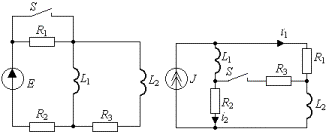
и) к) л) м)

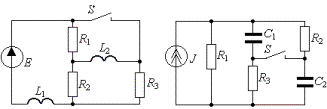
н) о) п) р)

Рис. 5п.

Таблица 4п

Вар.	Схе ма	E   В	J   А	L1   мГн	L2   мГн	C1   мкФ	C2   мкФ	R1   Ом	R2   Ом	R3   Ом	Опреде лить		Ключ   S
1	а	120	-	0.2	-	10	-	4	4	8	iC	i1	зам.
2	б	-	5	1	-	1	-	20	20	10	uC	iC	разм
3	в	120	-	10	-	10	-	100	500	500	iL	uL	зам.
4	г	-	10	1	-	500	-	2	2	6	uC	i2	разм
5	д	120	-	1	-	10	-	100	300	300	iL	u2	зам.
6	е	-	30	5	-	4	-	20	10	20	uC	iC	зам.
7	ж	60	-	2	-	5	-	10	10	10	iL	uL	разм
8	з	-	30	0.2	-	10	-	5	5	10	uC	iC	зам.
9	и	120	-	-	-	10	50	10	20	10	uC1	i1	разм
10	к	-	5	-	-	20	40	100	200	300	uC1	iC1	зам.
11	л	60	-	10	30	-	-	4	4	8	iL1	uL1	зам.
12	м	-	12	1	4	-	-	4	6	8	iL1	i1	зам.
13	н	120	-	2	8	-	-	4	4	8	iL1	uL1	разм
14	о	-	10	-	-	1	3	60	40	20	uC1	iC1	разм
15	п	80	-	1	5	-	-	8	4	4	iL1	uL1	зам.
16	р	-	2	-	-	10	20	50	150	200	uC1	iC1	разм
17	а	100	-	1	-	0.5	-	100	50	50	iL1	u2	разм
18	б	-	2	1	-	1	-	40	20	60	iL	uL	разм
19	в	100	-	10	-	1	-	40	60	60	uC	i3	разм
20	г	-	4	1	-	10	-	4	4	2	iL	uL	зам.
21	д	120	-	5	-	1	-	200	400	200	uC	u3	разм
22	е	-	4	10	-	1	-	30	20	10	iL	uL	зам.
23	ж	60	-	1	-	2	-	200	150	50	uC	u3	зам.
24	з	-	6	1	-	0.5	-	200	400	400	iL	i1	зам.
25	и	80	-	-	-	20	10	50	15	20	uC2	i2	зам.
26	к	-	6	-	-	4	2	100	200	100	uC2	u3	разм
27	л	30	-	5	15	-	-	5	15	5	iL2	u3	разм
28	м	-	12	4	2	-	-	20	4	6	iL2	i2	зам.
29	н	60	-	6	1	-	-	4	6	10	iL2	uL2	разм
30	о	-	4	-	-	20	10	40	20	60	uC2	iC2	зам.

 

Задание 5. Исследовать переходный процесс в цепи второго порядка (рис.5п; а - р) методом переменных состояния. Составить уравнения переменных состояния в послекоммутационной схеме для определения напряжений на емкостях и токов в индуктивностях в общем виде и в числах. Составить матрицу-столбец начальных значений переменных.

В цепи действует либо постоянный источник напряжения E, либо постоянный источник тока J. Параметры цепи указаны в таблице 4п.

По указанию преподавателя решить полученную систему на ЭВМ и вы-

вести результаты расчета в виде графиков на печать.

Приложение 4. Решение уравнений состояния электрической цепи.

 

Основным методом решения уравнений состояния является численный метод интегрирования с применением ЭВМ. В вычислительной математике существует большой набор алгоритмов численного решения систем дифференциальных уравнений, записанных в нормальной форме. В машинных программах наибольшее распространение получил метод Рунге-Кутта четвертого порядка с контролем точности вычислений на каждом шаге интегрирования и регулировкой шага вычислений.

В MATHCAD программа интегрирования по методу Рунге-Кутта носит имя rkfixed. Обращение к ней производится через операцию присваивания какой - либо переменной (здесь z) имени программы:

z: = rkfixed(x, 0, tk, N, D),

где x - вектор переменных состояния. Длина этого вектора - n задается предварительным описанием вектора начальных значений и соответствует числу уравнений состояния; 0 и tk - начало и конец временного интервала интегрирования; N - число точек на интервале интегрирования; z - матрица (массив), имеющая размер (N+1, n+1), где первый столбец (он же нулевой) соответствует дискретным значениям времени ti: zi0 = i.

Остальные столбцы - совокупность значений переменных состояния: zi1, zi2,…, zin, где индекс i изменяется от 1 до N; D - функция дифференцирования левой части системы уравнений, которая описывает правую часть уравнений, разрешенных относительно первых производных. Для линейных цепей эта функция имеет вид линейного матричного преобразования D(t, x):=A·x+F, где A - квадратная матрица коэффициентов, которые определяются структурой цепи и параметрами элементов; F - вектор независимых переменных, параметры которого определяются входными воздействиями, т.е. независимыми источниками питания цепи, которые могут изменяться во времени.

Элементы матриц A и F должны быть определены перед обращением к программе rkfixed. Для контроля правильности задания исходных данных можно (но не обязательно) обратиться к программе определения собственных чисел матрицы A: eigenvals(A). Эта программа выводит информацию о собственных числах, которые совпадают с корнями характеристического уравнения цепи. Необходимым (но недостаточным) условием правильности ввода данных является набор отрицательных собственных чисел, или комплексно-сопряженных с отрицательной вещественной частью.

 

Пример 1. Исследование переходного процесса в простейшей одноконтурной цепи второго порядка, которая образуется после отключения источника постоянного напряжения E от цепи. Эта задача рассмотрена в примере 3.5 для цепи (рис. 3.16а).

Параметры цепи: E = 40 В, r = 40 Ом, L = 1 Гн, C = 0,0005 Ф. Начальные значения переменных: u_C(0) = 40 B; i_L(0) = 1 А.

Уравнения состояния цепи для переменных u_C и i_L имеют вид

где x1 = zi1 = u_C, x2 = zi2 = i_L. Вектор внешних источников питания F отсутствует.

Перед обращением к программе интегрирования определяем (см. распечатку) через операцию присваивания следующие величины:

1. Коэффициенты матрицы A: a11: = 0; a12: = -2000; a21: = 1; a22: = -40;

2. Вектор начальных значений переменных x;

3. Число точек интегрирования N: = 500;

4. Формализованную матричную запись уравнений состояния (здесь без вектора F):

D(t, x): = A·x;

5. Правую границу временного интервала tk = 0,3 c.

Длительность участка интегрирования можно оценить по собственным числам матрицы A путем обращения к программе eigenvals(A). В этом примере имеем два комплексно-сопряженных числа p1 = -20+j40 и p2 = -20-j40, вещественные части которых одинаковы и равны b=-20 1/c. Эта часть комплексного числа определяет коэффициент затухания и непосредственно связана с длительностью переходного процесса формулой: tk = 3/b.

В рассматриваемом примере для наглядности интервал выбран в два раза большим: tk = 6/b = 6/20 = 0, 3 с.

Далее следует обращение к самой программе интегрирования и распе-чатка графика. Так как переменные состояния, измеряемые в разных единицах - в вольтах и в амперах, могут численно значительно отличаться друг от друга, то следует позаботиться о наглядности их графического изображения путем введения соответствующих масштабных коэффи-циентов. Здесь для переменной zi2 = x2 = i_L указан коэффициент 100. Чтобы получить истинное значение тока следует разделить численные значения оси ординат на 100 для этой переменной.

В соответствии с характером собственных чисел, переходный процесс носит колебательный характер, где обе переменные постепенно затухают до нулевого значения.

Обращение к программе rkfixed

 

a11:=0 a12:=-2000 a21:=1 a22:=-40 tk:=0.3 N:=500

D(t,x):=A·x

z:=rkfixed(x,0,tk,N.D)

i:=0..N

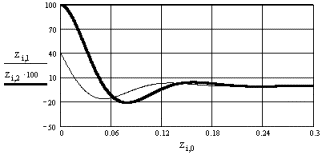
Пример 2. Исследование переходного процесса в цепи второго порядка, который возникает после подключения к цепи (рис. 3.13) сопротивления r1. Эта задача рассмотрена в примере 3.6, где были получены уравнения состояния цепи. Параметры цепи: J = 2 А; r1 = r2 = 50 Ом; L = 5 мГн; С = 0, 1 мкФ.

Уравнения состояния для переменных x1 = zi1 = u_C и x2=zi2= i_L имеют вид

Значения коэффициентов можно вычислить заранее и включить в программу в виде констант, или определить через операции присваивания в самой программе.

Значение N = 5000 указывается произвольно и влияет только на время и точность вычислений. Точность вычислений можно косвенно оценить, сравнив результаты интегрирования для двух значений N = N1 и N = N1/2. Если результаты практически совпадают, то точность вычислений и число точек интегрирования на интервале tk находятся в приемлемых пределах.

Через операцию присваивания определяются также вектор исходных значений x и вектор независимых источников F.

Временной интервал tk может быть указан произвольно или примерно определен параметрами цепи через анализ собственных чисел матрицы A. Следует выбрать наименьшее по модулю собственное число pмин. и воспользоваться формулой: tk = 3/pмин. В данном примере имеем p1 = -1, 888E5 1/c и p2 = -2, 118E4 1/с. Следовательно, tk = 3/2, 118E4 = 1, 42E-4 c.

Другой способ определения tk основан на анализе постоянных времени цепей первого порядка, которые можно построить на основе исходной цепи путем последовательного исключения реактивных элементов. Каждая такая цепь содержит один реактивный элемент, и для нее длительность переходного процесса определяется формулой tk=3·C·R , если это RC цепь, и tk=3·L/R если это LR цепь, где R - входное резистивное сопротивление цепи со стороны реактивности. Исключение индуктивности соответствует замене ее на короткозамкнутую перемычку, исключение емкости соответствует разрыву ветви, в которой стоит емкость. В данном примере имеем t0 = 3·L/(r1+r2) и t1=3·C·r1·r2/(r1+r2). Осуществляется процедура выбора из этих чисел наибольшего: tk: = max(t). Здесь это число равно tk = 1, 5E-4, что практически совпадает с ранее полученным значением.

Формализованная матричная запись уравнения состояния определена в самой общей форме с учетом вектора внешних воздействий: D(t, x)=A·x+F.

Распечатка графиков произведена с учетом введения масштабного коэффициента 100 для переменной zi2 = i_L. Переходный процесс носит апериодический характер. Напряжение на емкости изменяется от уровня u_C(0-) = 100 B до уровня u_Cпр. = 50 В. Ток в индуктивности изменяется от значения i_L(0-)=2 А до значения i_Lпр. = 1 А. Можно отметить в решении точки экстремума и перегиба функций.

 

Обращение к программе rkfixed

 

J:=2 r1:=50 r2:=50 L:=5·10^-3 C:=1·10^-7 N:=5000

D(t, x):=A·x+F tk:=max(t)

tk=1.5 10^-4

z:=rkfixed(x, 0, tk, N, D)

i:=0..N

 

Пример 3. Исследование переходного процесса в цепи третьего порядка (рис. 3.23), который возникает после подключения к цепи сопротивления r5. Переходный процесс обеспечивается независимым источником напряжения Е, а также энергией электромагнитного поля, запасенной в индуктивностях L1 и L2 и емкости C. Параметры цепи:

Е = 120 В; r1 = r3 = r4 = 1 Ом; r2 = 2 Ом; r5 = 2 Ом; L1 = 1 мГн; L2 = 2 мГн;

C=10 мкФ. Уравнения состояния цепи для этой задачи получены в примере 3.7. Переменными состояния будут x1=zi1=u_C, x2=zi2=i_L1 и x3=zi3=i_L2. Система уравнений в данном случае имеет вид

где определена промежуточная переменная g:=1/(r3+r4+r5), а также сами коэффициенты aij: a11:=-g/C; a12:=g·(r4+r5)/C; a13:=-g·r5/C; a21:=-g·(r4+r5)/L1; a22:=-g·(r1·r5+r3·r4+r3·r5+r1·r3+r1·r4)/L1; a23:=g·r3·r5/L1; a31:=g·r5/L2; a32:=g·r3·r5/L2; a33:=-(r2+(r3+r4)·r5·g)/L2.

Параметры вектора независимых источников: f1: = 0; f2: = E/L1; f3: =0.

Вектор начальных значений переменных может быть введен в виде формул или числами x:= (90 30 30)^T.

Вывод информации о собственных числах матрицы A позволяет судить о характере переходного процесса; он апериодический, так как собственные числа все вещественные и отрицательные. По этим числам выбирается время переходного процесса как утроенное значение обратной величины от наименьшего по модулю собственного числа: tk: = 3/(min(li)). В рассматриваемом примере это число l3 = 1, 268E3. Тогда tk = 2E-3 c.

Остальные операторы и обращение к программе интегрирования такое же, как и в рассмотренных ранее примерах.

 

Обращение к программе rkfixed

 

E:=120 r1:=1 r2:=2 r3:=1 r4:=1 r5:=2 L1:=1·10^-3 L2:=2·10^-3 C:=1·10^-5 N:=5000

D(t, x):=A·x+F

tk:=2.366·10^-3

 

z:=rkfixed(x, 0, tk, N, D)

i:=0..N

 

ИСТОРИЯ РАЗВИТИЯ ЭЛЕКТРОТЕХНИЧЕСКОГО ОБРАЗОВАНИЯ В ИНСТИТУТЕ ТОЧНОЙ МЕХАНИКИ И ОПТИКИ

 

При реорганизации в 1930 году техникума точной механики и оптики в учебный комбинат, состоящий из института, техникума и ФЗУ в системе Всесоюзного объединения оптико-механической промышленности, руководство комбинатом уделяло достаточно большое внимание качеству преподавания дисциплин электротехнического цикла, приглашая на работу известных ленинградских профессоров-электротехников.

В те годы электротехническую подготовку в нашем институте проводи-ли кафедры «Электротехники» и «Электроизмерительные приборы». Кафедрой «Электротехники» руководил профессор Салтыков Лев Николаевич, а кафедрой «Электроизмерительные приборы» профессор Шишелов Л.П.

С 21 ноября 1937 года до эвакуации института кафедрой заведовал Александр Александрович Солодовников, который являлся в те годы известным специалистом в области электротехники и электроизмери-тельных приборов.

Во время войны при эвакуации ЛИТМО в г. Черепаново и после возвращения из эвакуации кафедрой руководил доцент, кандидат технических наук Березниковский Сергей Федорович.

В послевоенные годы в Ленинграде, да и в целом по стране, ощущался острый дефицит опытных преподавателей высшей школы, и руководство институтом принимает решение о приглашении в институт для работы по совместительству и исполнения обязанностей заведующего кафедрой «Общей и специальной электротехники» известного ученого, педагога и методиста Людвига Мариановича Пиотровского, в то время заведующего аналогичной кафедрой в Политехническом институте и автора известных монографий: «Электрические машины» в двух частях 1957 и 1958 года издания, написанная в соавторстве с академиком АН СССР Костенко М.П., позднее дважды переизданная в 1965 и 1973 годах, «Трансформаторы» 1934 года издания, «Испытания электрических машин» в двух частях 1937 и 1938 года издания, «Электрические машины» (для учащихся техникумов) 1949 года и т.д.

В 1948 году на базе бывшей кафедры «Общей и специальной электротехники» образуются три кафедры: «Общей электротехники и электрических машин», зав.каф. доцент Березниковский С.Ф., «Теоретических основ электротехники», зав. каф. профессор Слепян Л.Б., «Электроизмерительных приборов» и.о. зав. каф. профессор Слепян Л.Б., но в том же 1948 году кафедра «Электроизмерительных приборов» расформируется и ее штаты передаются на кафедру «Автоматики и телемеханики».

В 1951 году кафедры «Электротехники» и «ТОЭ» объединяют в единую кафедру «Электротехники и ТОЭ» в составе Радиотехнического факультета, под руководством доцента Березниковского С.Ф.

В 1953 году зав. кафедрой становится доцент Сочнев Алексей Яковлевич. А в 1956 году в составе Радиотехнического факультета вновь образуются две кафедры – «ТОЭ» зав. каф. Доцент Сочнев А.Я., «Электрических машин» зав.каф. доцент Березниковский С.Ф.

В 1961 года в связи со смертью доцента Березниковского С.Ф. в ЛИТМО приглашают проф. Сахарова А.П. , который в мае этого же года избирается на должность зав. каф. «Электрических машин».

В 1965 году на должность заведующего кафедрой «Электрические машины» избирается доцент, к.т.н. Глазенко Т.А. и в 1968 году приказом Министра Высшего и Среднего образования СССР № 854 от 29 ноября кафедры «ТОЭ» и «Электрических машин» объединяются в единую кафедру «Электротехники».

Профессор Глазенко Т.А. являлась одним из наиболее ярких воспитанников Ленинградской электротехнической школы, она в 1948 году с отличием закончила энергетический факультет Ленинградского института инженеров железнодорожного транспорта и начала работать в институте механизации и электрификации сельского хозяйства на кафедре общей и теоретической электротехники. После прохождения одногодичной аспирантуры в декабре 1953 года защитила диссертацию и получила степень кандидата технических наук, а в 1966 году докторскую диссертацию и более 25 лет возглавляла кафедру.

Татьяной Анатольевной Глазенко в эти годы по существу была создана Ленинградская школа по силовой электроники, специалисты которой успешно решали задачи определения электрофизических параметров силовых приборов, задачи по созданию высокоэффективных алгоритмов коммутации коммутирующего оборудования в современных системах электропривода и источниках питания.

В 1990 году на должность заведующего кафедрой избирается профессор, д.т.н. Герман - Галкин Сергей Германович, а в 1991 году доцент Томасов Валентин Сергеевич.

В 1993 году приказом № 196 Государственный комитет РФ по высшему образованию дополнил перечень направлений базового высшего образова-ния нашего университета направлением 654500 - “Электротехника, электромеханика и электротехнологии” с дальнейшим продолжением выпуска инженеров по специальностям 1801: “Электромеханика» и 1804: «Электропривод и автоматика».

В связи с тем, что кафедра стала совмещать преподавание специальных дисциплин с традиционными для нее, электронно-электротехническими дисциплинами общетехнического цикла для базовых направлений университета: оптотехника и приборостроение, она была в 1996 году переименована в кафедру электротехники и прецизионных электро-механических систем (Э и ПЭМС).

Список литературы

 

1. Осипов Ю.М., Петров Е.А. Анализ разветвленных цепей постоянного и переменного тока. Учебное пособие. - СПбГИТМО (ТУ), 1998.

2. Бессонов Л.А. Теоретические основы электротехники. Электрические цепи. - М.: Высшая школа, 1978.

3. Матханов П.Н. Основы анализа электрических цепей. Линейные цепи. - М.: Высшая школа, 1980.

4. Белецкий А.Ф. Теория линейных электрических цепей. Учебник для вузов. - М.: Радио и связь, 1986.

5. Новгородцев А.Б. 30 лекций по теории электрических цепей. Учебник для вузов. - СПб.: Политехника, 1995.

6. Глазенко Т.А., Прянишников В.А. Электротехника и основы электроники. Учебное пособие для вузов. - М.: Высшая школа, 1985.

7. Прянишников В.А. Теоретические основы электротехники. Курс лекций. – СПб.: ”КОРОНА принт”, 2000.

 

124