3.4 Уравнения состояния электрической цепи

Для электрических цепей более высокого порядка (n > 2), включающих

емкостей и индуктивностей, переходные процессы исследуются путем составления и решения системы уравнений состояния. При этом предполагается, что цепь состоит из набора канонических ветвей и имеет место независимость всех переменных состояния друг от друга. Как было отмечено ранее, под переменными состояния понимают напряжения на емкостях и токи в индуктивностях . Общий путь расчета в этом методе основан на составлении дифференциальных уравнений первого порядка относительно переменных состояния , записанных в нормальной форме Коши

Коэффициенты в правых частях уравнений состояния определяются структурой цепи и параметрами ее элементов, а функции учитывают влияние внешних независимых источников энергии на скорость изменения каждой переменной состояния. Переменные состояния однозначно определяют запас энергии цепи в любой момент времени, а, следовательно, через эти переменные однозначно определяются остальные токи и напряжения.

Для линейных цепей система уравнений состояния также линейна, и ее обычно записывают в матричной форме

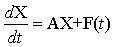
(3.30)

где X - вектор переменных состояния; A - квадратная матрица; F(t) - вектор входных воздействий.

Эта система полностью определяет поведение цепи в переходном режиме. Формирование системы уравнений (3.30) основано на известных дифференциальных соотношениях (3.21), из которых непосредственно записываются производные от переменных состояния

Если выразить правые части этих соотношений как функции всех переменных состояния и внешних источников воздействий, то это позволит сформировать систему уравнений (3.30). Для этой цели можно использовать законы Кирхгофа или метод наложения.

3.4.1 Использование законов Кирхгофа

  При составлении уравнений состояния следует иметь в виду, что любая переменная состояния характеризует энергию электрического или магнитного поля, запасенную реактивным элементом, и по теореме компенсации может быть заменена либо источником напряжения, либо источником тока. Этот прием уже был использован выше в определении неосновных начальных условий в классическом методе расчета переходных процессов. При записи уравнений состояния этот прием получает дополнительное развитие: исходная цепь заменяется на чисто резистивную, где вместо реактивных элементов действуют независимые источники тока и напряжения. С течением времени структура цепи не меняется, но численные значения источников изменяются вслед за изменением переменных состояния.

Фактически на каждом шаге интегрирования приходится решать задачу расчета резистивной цепи постоянного тока при неизменной структуре цепи и изменяющимися источниками энергии. Найденные на предыдущем шаге переменные состояния служат для следующего шага интегрирования начальными условиями. Процесс интегрирования начинается с вектора начальных значений переменных состояния X(0), который находят на основании законов коммутации, рассматривая напряжения на емкостях и токи в индуктивностях в момент времени t = 0-.

При изображении источников, заменяющих реактивные элементы, необходимо соблюдать некоторые правила, которые следуют из теоремы компенсации. Эти правила указаны на рис.3.20. Емкость С заменяется на источник напряжения с ЭДС , направленной в сторону разряда емкости на внешнюю цепь, т.е. от минуса к плюсу; при этом направление тока в емкости сохраняет свое прежнее направление. Индуктивность L заменяется на источник тока , направленный в сторону принятого ранее положительного направления тока; при этом направление напряжения на индуктивности сохраняет свое прежнее направление. Все условные положительные направления токов и напряжений в исходной цепи должны быть заранее указаны, они же и сохраняются в преобразованной цепи.

Рис. 3.20.

 

Законы Кирхгофа можно использовать для сравнительно простых цепей, где число резистивных элементов минимально. Рассмотрим задачу составления системы уравнений на примере одноконтурной цепи.

  Пример 3.5. Составить уравнения состояния для цепи рис.3.16а, рассмотренной в примере 3.4.

На рис.3.21 изображена схема исследуемой одноконтурной цепи, которая полностью отражает взаимодействие реактивных и резистивных элементов цепи в любой момент времени t после коммутации. При изображении использована замена емкости С на источник напряжения , а индуктивности L на источник тока в соответствии с рис.3.20.

Рис. 3.21. Эквивалентная схема замещения цепи (t>0)

 Полученная схема обобщает задачу определения неосновных начальных условий, которая анализировалась в примере 3.4 для момента времени t=0+ .После замены реактивных элементов цепь стала чисто резистивной, и для нее легко написать уравнения равновесия по первому и второму закону Кирхгофа

или

или

Объединяя уравнения в систему, получим

или

Для того чтобы ЭВМ начала процесс интегрирования этой системы уравнений, необходимо указать вектор начальных значений, который включает два числа: напряжение на емкости и ток в индуктивности к моменту коммутации.

Задача решена.

В Приложении 4 выполнен процесс интегрирования полученной системы уравнений на ПЭВМ (см. пример 1).

  Пример 3.6. Составить уравнения состояния для цепи рис.3.13а.

На рис.3.22 изображена схема замещения цепи после коммутации (ключ S замыкается), которая обобщает схему рис.3.15б и эквивалентно отражает энергетическое состояние цепи в любой момент времени t.

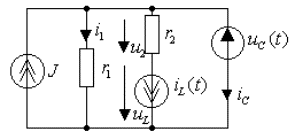
Рис. 3.22. Эквивалентная схема замещения цепи (t>0)

 

На основании первого закона Кирхгофа выразим ток в емкости в зависимости от токов других ветвей, подходящих к узловой точке. При этом необходимо ток в резистивном элементе связать с переменными состояния

где 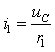или

На основании второго закона Кирхгофа составим уравнение равновесия напряжений для контура k, в котором в явном виде наблюдается влияние обеих переменных состояния. При этом следует напряжение на резистивном элементе выразить через переменные состояния

где или

Объединяя уравнения в систему, получим

или

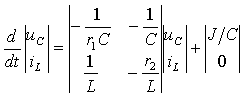
Вектор начальных значений сформируем на основе анализа докоммутационного состояния цепи

где ;

Задача решена.

  Интегрирование системы уравнений состояния на ПЭВМ приведено в Приложении 4 (см. пример 2).

  Как показывают рассмотренные примеры, составление уравнений состояния базируется на законах Кирхгофа и компонентных уравнениях цепи. В первоначальном виде эти уравнения содержат ряд избыточных переменных - токов и напряжений в резистивных элементах цепи. Так в примере 3.5 это напряжение , а в примере 3.6 это ток и напряжение . Для получения нормальной формы записи уравнений необходимо, во-первых, выразить эти избыточные переменные через переменные состояния, во-вторых, скомпоновать уравнения таким образом, чтобы в каждое из них входил бы только один член с производной от переменной состояния. Отсюда следует, что контура, для которых составляются уравнения равновесия для напряжений должны включать только одну индуктивность, а узловые точки (или сечения) - только одну емкость. Этот путь анализа не всегда прост в исполнении, и требует некоторого опыта. Задача усложняется с увеличением числа резистивных элементов, контуров и узловых точек [3],[5].