7.6. Тепловое расширение твердых тел

Рассмотрим простую модель, состоящую из двух атомов. Будем считать, что между атомами действует упругая сила взаимодействия. Кривая потенциальной энергии взаимодействия представлена на рис.7.8 и меняется по закону где коэффициент квазиупругой силы.

При температуре атомы колеблются так, что межатомное расстояние меняется от до со средним значением , при межатомное расстояние меняется от до со средним значением и т.д. Кривая потенциальной энергии симметрична относительно прямой , и среднее межатомное расстояние не зависит от амплитуды колебаний и остается постоянным при любой температуре.

Однако, в реальных кристаллах силы взаимодействия между атомами в решетке нельзя считать абсолютно упругими, как мы предполагали ранее, они зависят от смещения атомов из положения равновесия не линейно, а содержат ангармонические члены, влияние которых возрастает с ростом температуры. Тепловое расширение решетки (или изменение равновесного объема V при изменении температуры) обусловлено асимметрией взаимодействия между атомами, вызванной тем, что сила отталкивания возрастает быстрее при сближении атомов, чем сила притяжения при их удалении друг от друга. 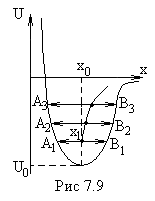Это приводит к непараболическому виду кривой потенциальной энергии взаимодействия (рис.7.9). При температуре атомы колеблются так, что межатомное расстояние меняется от до со средним значением , при межатомное расстояние меняется от до со средним значением и т.д. и твердое тело с повышением температуры расширяется. Среднее расстояние между атомами определяется выражением:

где g – коэффициент ангармоничности колебаний атомов; - коэффициент упругости.

Таким образом, с ростом температуры увеличивается не только амплитуда колебаний атомов, но также происходит увеличение средних расстояний между ними, что ведет к расширению твердого тела.

Коэффициент линейного теплового расширения для данного вещества зависит от коэффициента ангармоничности g, коэффициента упругости , т.е. определяется свойствами вещества.

7.7. Теплопроводность твердых тел Диэлектрики

Все тела способны проводить теплоту. В изотропном твердом теле распространение теплоты подчиняется закону Фурье

= - ,

где – поверхностная плотность теплового потока. Это вектор, модуль которого равен тепловому потоку через единичное сечение, перпендикулярное , Т – температура, – градиент температуры вдоль нормали к изотермической поверхности; - теплопроводность.

Знак «минус» показывает, что теплота течет в направлении, противоположном градиенту температуры, т.е. от горячей области к холодной.

В диэлектриках теплота распространяется посредством атомных колебаний (фононный механизм).

А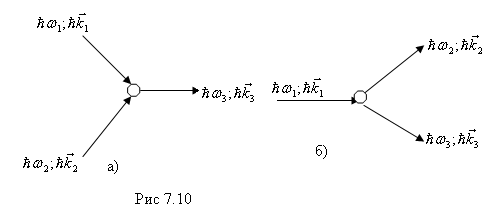 томы в твердом теле связаны между собой. При нагревании какого-либо участка тела амплитуда колебаний атомов этого участка увеличивается, и атомы при своем движении толкают соседние атомы, которые в свою очередь передают это движение своим соседям, и т. д. Кинетическая энергия колебаний атомов передается от нагретого участка к более холодному. Макроскопический поток кинетической энергии атомов – теплообменный поток. Этот процесс одинаков с процессом распространения упругих звуковых волн в твердом теле. При объяснении явлений теплопроводности мы уже не можем считать, что атомы совершают строго гармонические колебания, которые распространяются в кристалле в виде системы невзаимодействующих между собой упругих волн. Такие волны распространялись бы в кристалле без затухания, следовательно, имели бы неограниченный свободный пробег, тепловой поток даже при малых градиентах температуры мог бы существовать сколь угодно долго, и теплопроводность была бы бесконечной (тепловое равновесие не устанавливалось бы). В реальных же твердых телах теплопроводность конечна. Это связано с тем, что колебания атомов кристаллической решетки не являются чисто гармоническими из-за того, что силы взаимодействия между атомами линейно зависят от смещения атомов. Ангармонический характер колебаний учитывают, выводя дополнительные слагаемые в значение потенциальной энергии. Тем самым учитывают рассеяние фононов друг на друга, которое сопровождается рождением и исчезновением фононов – либо два фотона превращаются в один, либо фонон распадается на два (рис.7.10).

При этом должны выполняться два условия:

, , (7.12)

где , - вектор обратной решетки. Первое из уравнений (7.12) представляет собой закон сохранения энергии для трехфононного процесса. Фонон с волновым вектором и частотой , вообще говоря, не обладает механическим импульсом, как обычная микрочастица. Однако величина , называемая квазиимпульсом, во многом сходна с импульсом. При выражение (7.12) совпадает с законом сохранения импульса. Взаимодействие, при котором называется нормальным или N-процессом. Этот процесс аналогичен процессу взаимодействия элементарных частиц, при котором выполняются законы сохранения энергии и импульса.

В отличие от взаимодействия обычных микрочастиц при взаимодействии фононов общее число фононов не сохраняется, а квазиимпульс может сохраняться лишь с точностью до значения обратной решетки. Это означает, что кристаллическая решетка, в которой движутся фононы, тоже принимает участие в столкновениях, забирая часть импульса, равную . Взаимодействие, при котором называется процессом переброса или U-процессом. В процессах переброса энергии должна сохраняться так же, как и в нормальных процессах.

После N-процесса тепловая энергия переносится в направлении групповой скорости фонона, поэтому в случае N-процесса направление потока энергии в моде с волновым вектором совпадает с направлением, в котором энергия эффективно переносится модами и . В такой ситуации N-процессы сами по себе не приводят к восстановлению равновесного распределения фононов, а это означает, что конечный перенос энергии может сохраняться и при отсутствии градиента температуры, т.е. теплопроводность бесконечно велика.

После U- процесса тепловая энергия передается в направлении, которое не совпадает с направлением групповых скоростей в модах и . Такие существенные изменения волнового вектора всегда ведут к восстановлению равновесного распределения фононов, а, следовательно, и к конечному значению теплопроводности.

Рассмотрим зависимость теплопроводности от температуры. Из кинетической теории газов в предположении, что вместо движения молекул рассматривается движение фононов, получаем

где -теплоемкость единичного объема кристалла, связанная с колебаниями решетки, - средняя скорость фононов, примерно равная скорости звука в кристалле и слабо зависящая от температуры, - средняя длина свободного пробега фонона, - эффективное время релаксации, обратное значение которого соответствует частоте столкновений фононов.

Зависимость теплопроводности от температуры определяют величины и . При высоких температурах удельная теплоемкость приближается к предельному значению, определяемому законом Дюлонга и Пти, ,т.е. становится независящей от температуры, и зависимость теплопроводности от температуры определяется температурными изменениями длины свободного пробега фононов. Число фононов при таких температурах велико и пропорционально температуре:

поэтому вероятность возникновения процессов переброса увеличивается с ростом температуры, и частота столкновений растет пропорционально температуре, а, соответственно длина свободного пробега фононов уменьшается обратно пропорционально температуре: . Тогда .

При понижении температуры среднее число фононов, способных принять участие в процессах переброса, спадает по экспоненте:

вероятность процессов переброса уменьшается тоже по экспоненте, и длина свободного пробега (как и время релаксации) фонона с понижением температуры увеличивается экспоненциально

У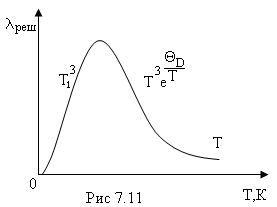 дельная теплоемкость с понижением температуры уменьшается в соответствии с законом Дебая, как , но рост теплопроводности происходит преимущественно за счет , которая растет по экспоненте,

При приближении температуры к абсолютному нулю вероятность процессов переброса становится малой, длина свободного пробега становится сравнимой с размерами образца и не зависит от температуры. При дальнейшем понижении температуры коэффициент теплопроводности резко спадает до нуля, так же, как теплоёмкость, т.е. как . Зависимость теплопроводности диэлектриков от температуры представлена на рис.7.11.