4.5. Энергетический спектр электронов в кристалле. Модель Кронига-Пенни

Для нахождения энергетического спектра электронов в кристалле необходимо решить одноэлектронное уравнение Шредингера с периодическим потенциалом решетки . Собственные функции и собственные значения энергии этого уравнения зависят от вида периодического потенциала.

Некоторые характерные особенности энергетического спектра можно узнать, рассматривая простую одномерную модель периодического потенциала, предложенную Р. Кронигом и В.Пенни.

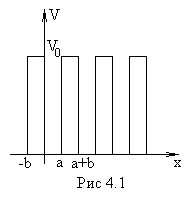Зависимость потенциальной энергии V электрона от расстояния х для одномерной решетки в этой модели представлена на рис.4.1.

Прямоугольные потенциальные ямы шириной а чередуются с прямоугольными барьерами шириной b.

Период такой решетки .

Потенциальная энергия представляет собой функцию

Здесь п- любое число ( ).

Решение одноэлектронного уравнения Шредингера для одномерного случая и потенциальной энергии приводит к уравнению

. (4.7)

Здесь Р – степень прозрачности барьера для электрона, т.е. степень связанности электрона в потенциальной яме, . (4.8)

В уравнении (4.7)

• cos k - функция четная,

• замена волнового числа k на –k не меняет уравнения.

Это означает, что энергия электрона также является четной функцией k,

т.е.

На рис.4.2 изображена зависимость левой части уравнения (4.7) от параметра

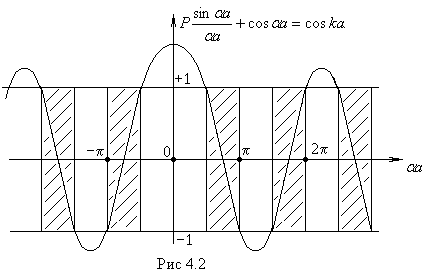
• . Поскольку cos k , стоящий в правой части уравнения (4.7), может принимать значения только в интервале от +1 до -1, то допустимыми значениями являются такие, для которых левая часть уравнения не выходит из указанных пределов.

• интервалы разрешенных значений заштрихованы.

Ширина этих интервалов зависит

- от параметра Р:- чем меньше Р, тем они шире.

- от . При любом зафиксированном значении Р эти интервалы расширяются с увеличением . В силу соотношения (4.8) между и энергией электрона Е сказанное относится и к энергии.

Таким образом, энергия электрона в кристалле не может принимать любого значения. Есть зоны разрешенных и зоны запрещенных энергий.

р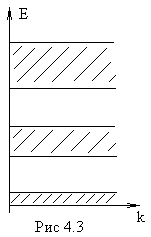 ис.4. 3: Чередование разрешенных и запрещенных зон

Рассмотрим, как изменяется энергетический спектр в двух предельных случаях и .

• Случай соответствует условию , т.е. почти свободному электрону (приближение слабой связи).

Из (4.7) получаем , т.е. ,

и на основании (4.8):

Это выражение совпадает с зависимостью E(k) для свободного электрона.

Поскольку на k в этом случае никаких ограничений не накладывается, кривая E(k) представляет собой непрерывную параболу.

• случай в силу того, что . Это означает, что электрон локализован в бесконечно глубокой яме, т.е. сильно связан (приближение сильной связи). При из уравнения (4.7) находим, что т.е. , (4.9)

где М=

а из (8) . (4.10)

Таким образом, при система энергетических зон вырождается в дискретные уровни.

Попытаемся теперь найти явный вид закона дисперсии E(k) для электрона, движущемся в периодическом поле решетки.

Для этого надо решить относительно Е уравнение (4.7).

Это можно сделать только приближенно.

Допустим, что Р>>1 - это соответствует приближению сильной связи.

Для больших Р согласно (4.9) можно записать: , (4.11)

где .

Разлагая левую часть уравнения (4.7) в ряд и ограничиваясь линейными относительно членами, получим ,

или (4.12)

Подставляя (4.12) в (4.11), находим (4.13)

Учитывая связь между и энергией электрона Е (4.8) и ограничиваясь линейными относительно членами при возведении (4.13) в квадрат,

получим выражение, связывающее Е и k: (4.14)

или (4.15)

Здесь обозначено ;

- коэффициент перед , в общем случае не равный .

Первый член в (4.15) представляет собой энергию М-го энергетического уровня электрона в изолированной бесконечно глубокой потенциальной яме, определяемую формулой (4.10).

Второй и третий члены связаны действием периодического поля решетки.

Видно, что в периодическом поле решетки энергетические уровни опускаются на значение С (перед С стоит знак «—»!). Это свидетельствует о том, что объединение атомов в цепочку энергетически выгодно.

Третий член в (4.15) определяет зонный характер энергетического спектра, поскольку cos ka ограничивает пределы его изменения.

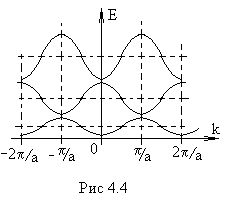На рис.4. 4 показана зависимость E(k) для электрона, находящегося в одномерной решетке.

Здесь наглядно видно, что

• для всех k, отличающихся на (2 / )n, энергия одна и та же.

• Интервал значений k от до представляет собой первую зону Бриллюэна.

• два отрезка от до и от до 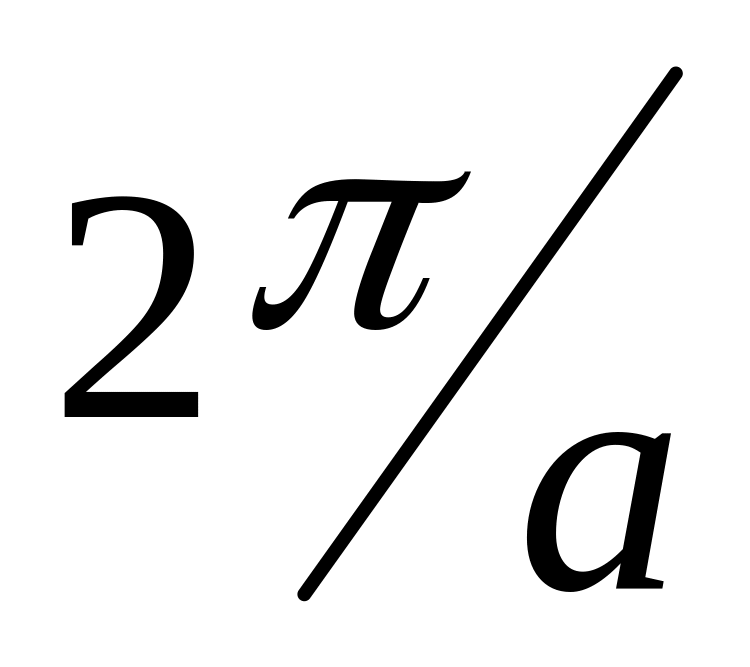- вторую зону Бриллюэна и т.д.

В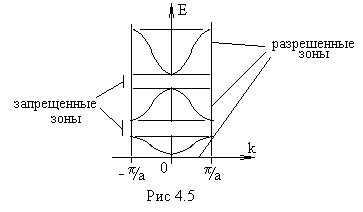 се возможные значения энергий в каждой энергетической зоне можно получить путем изменения k в пределах первой зоны Бриллюэна.

Поэтому зависимость E(k) часто строят только для первой зоны Бриллюэна. Все остальные значения Е могут быть приведены в эту зону.

Такой способ изображения E(k) , иллюстрируемый на рис.4.5, получил название схемы приведенных зон .

В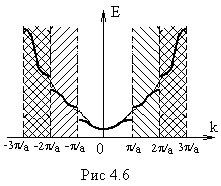 отличие от него зависимость, показанную на рис.4.4, называют периодической зонной схемой.

Кроме этих двух способов изображения энергетических зон используют ещё один способ, получивший название расширенной зонной схемы (рис.4.6).

Здесь

• различные энергетические зоны размещаются в k-пространстве в различных зонах Бриллюэна.

• показана также параболическая зависимость E(k) для свободного электрона. Начало отсчета энергий обеих зависимостей совмещено.

Из рис.4. 4 хорошо видно, что

• в каждой нечетной энергетической зоне, т. е. в каждой зоне, определяемой числами М=1, 3, 5, ..., имеется

- один минимум энергии в центре зоны Бриллюэна

- и два эквивалентных максимума на краях зоны Бриллюэна.

• В четных энергетических зонах наоборот

- максимум энергии в центре каждой зоны Бриллюэна,

- минимумы.- на границах.

• Разрывы в энергетическом спектре электрона появляются при достижении волновым вектором k значений n /а, т. е. на границах зон Бриллюэна.

Какова физическая природа этих разрывов?

Выразим волновой вектор через длину волны электрона

и запишем условие, при котором функция E(k) терпит разрыв:

или . (4.16)

Последнее выражение представляет собой условие Вульфа — Брэгга для электронной волны, падающей на решетку перпендикулярно атомным плоскостям.

При выполнении этого условия функция Блоха представляет уже не бегущую, а стоячую волну, так как электрон с таким волновым вектором при его движении (в реальном пространстве) испытывает брэгговское отражение.

Падающая и отраженная волны могут складываться двумя способами, образуя симметричную и антисимметричную комбинации:

(4.17)

( 4.18)

Выражения (4.17) и (4.18) записаны для значений волновых векторов k= / .

Волновая функция не изменяется при замене х на - х, a меняет знак.

Функция является мнимой, однако плотность электрического заряда, связанная с волновой функцией в этом случае, так же как и для представляет собой вещественную отрицательную величину.

В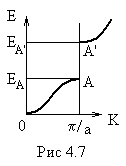 олновым функциям и ₂ соответствуют разные энергии.

• Решению , отвечает меньшая энергия, которая соответствует верхней границе первой зоны (точка А на рис. 4.7),

• а решению - энергия, соответствующая нижней границе второй зоны (точка ).

• При k< /a электрон обладает энергиями меньшими, чем ,

• а при k> a - энергиями, большими, чем .

• В интервале от до нет ни одного собственного значения энергии электрона, т. е. эта область представляет собой запрещенную зону.

Напомним, что, рассматривая колебания цепочки атомов, мы также пришли к выводу, что при достижении волновым вектором границы зоны Бриллюэна, т. е. k = / , наблюдается отражение упругих и образование стоячих волн. Эти стоячие волны являются результатом сложения двух бегущих волн, распростра­няющихся в противоположных направлениях.

В трехмерном случае зонная структура здесь может быть значительно сложнее, чем в рассмотренной выше одномерной модели. Зависимость Е(k) в трехмерном кристалле может быть различна для разных направлений в зоне Бриллюэна. Это связано с тем, что трехмерный потенциал V(r), зависящий от структуры кристалла, в различных направлениях не одинаков. Следствием этого может быть перекрытие разрешенных зон.

Так, например, запрещенная зона в одном направлении может совпадать с разрешенной зоной в другом направлении. Перекрытие разрешенных зон нельзя получить в одномерном случае.