2. Статистическая корреляционная функция и ее аппроксимация

При экспериментальном исследовании случайного процесса первичным материалом является выборка, представляющая дискретные значения процесса, взятые через постоянные интервалы времени . Пусть весь интервал времени наблюдения процесса равен . Разделим этот интервал на равных частей , тогда . Непрерывное время заменим дискретными значениями , где . Непрерывное время (аргумент корреляционной функции) представим как , где Значения случайного процесса в дискретные моменты времени обозначим 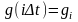, а значения корреляционной функции - через . Дискретные значения корреляционной функции могут быть приближенно определены по формуле

. (7)

Функция называется статистической корреляционной функцией. Она лишь приближенно соответствует действительной корреляционной функции, определяемой формулой (1). В формуле (1) интервал наблюдения , а в реальной выборке всегда конечно. Чем больше , тем меньше погрешность определения .

Вычисления по формуле (7) следует выполнять на ЭВМ. Значения изменять от 0 до 40, . Результаты вычислений вписать в табл. 3.

Т а б л и ц а 3

K	0	1	2	3	. . .		. . .	39	40
Rg*(k)

Другой важной характеристикой случайного процесса является его математическое ожидание (среднее значение). Оценка математического ожидания процесса по его выборке определяется по формуле

. (8)

В зависимости от характера случайного процесса его статистическая корреляционная функция может быть приближенно аппроксимирована одним из следующих выражений:

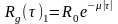, (9)

, (10) . (11)

Используются и другие выражения.

Следует иметь в виду, что график , полученный обработкой некоторой реализации конечной длительности, содержит элемент случайности, который может оказать существенное влияние при больших . Поэтому следует добиваться хорошего совпадения экспериментальной и аналитической кривых прежде всего на начальном участке значений аргумента до , начиная

Рис. 1. а) Статистическая корреляционная функция;

b) ее аппроксимация

с которого, не выходит за пределы (0,3-0,5) .

По виду графика следует выбрать соответствующую аппроксимирующую функцию, а затем определить ее параметры таким образом, чтобы графики и максимально совпадали.

Наиболее качественным методом определения неизвестных значений параметров является метод наименьших квадратов, однако его использование требует сложных вычислений. В данной курсовой работе рекомендуется определить неизвестные параметры аппроксимирующего выражения из условия равенства его ординат кривой в некоторых характерных точках. Такими могут быть, например, ; значения при которых и др.

Рассмотрим пример. Пусть имеет вид, как показано на рис. 1. Для аппроксимации этого графика выберем формулу (10).

Необходимо определить параметры . Очевидно . Пусть первое пересечение графиком оси абсцисс происходит в точке_(рис.1). Тогда , откуда следует:

.

Для определения выберем произвольную точку на начальном участке кривой . Пусть координаты точки соответственно равны . Подставим эти координаты в формулу аппроксимирующей функции:

_.

Из последнего уравнения следует

.

В тех случаях, когда R₀ получить невозможно путем обработки экспериментальных данных, что имеет место, например, при проведении расчетов в пакете MATLAB, можно воспользоваться для определения 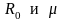двумя фиксированными точками статистической корреляционной функции, например, первой и шестой. Подставив в формулу (10) параметры, соответствующие первой и шестой точкам статистической корреляционной функции, получим два уравнения:

(12)

(13)

_{Разделив первое уравнение на второе, получим:} .

Из последнего выражения находим µ: .

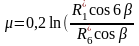Подставив найденное значение µ в (12) определим R₀: