9.4. Модель з імовірнісними обмеженнями

Підводячи підсумки розгляду викладеного в попередньому розділі методу рішення двокрокової стохастичної задачі лінійного програмування, приходимо до висновку, що основний недолік цього методу полягає у тому, що отримувана в результаті його застосування стандартна лінійна модель (еквівалентна вихідній стохастичній моделі) має занадто велику розмірність.

Збільшення розмірності обумовлене тим, що для побудови вичерпних правил ухвалення рішення на другому кроці необхідно враховувати всі можливі значення випадкових показників, що фігурують у задачі. Якщо, однак, зробити ряд додаткових припущень, що спрощують, то можна побудувати інший, простіший метод рішення, який дозволяє звести двокрокову лінійну стохастичну модель до звичайної лінійної оптимізаційної моделі тієї ж розмірності. Цей метод називають програмуванням з імовірнісними обмеженнями. Пояснимо його сутність на прикладі, уже розглянутому в попередньому розділі.

Приклад. Звернемося знову до задачі фірми. Спробуємо спростити цю задачу в ще більшій мірі, припустивши, що коефіцієнти а₁ і а₂ є відомими, а замість строгої вимоги повної реалізації надлишкової продукції будемо припускати, що можливими є альтернативні варіанти дій, економічні наслідки яких не визначені. Тоді випадковими величинами будуть лише ринкові ціни r_j та граничні значення для рівнів попиту D_і. При цьому для очікуваного значення питомого прибутку будемо мати де означає номер продукції, що випускається фірмою.

Підлягаючої максимізації цільова функція має вигляд

Максимізувати . (9.30)

Помітимо, що вираз для цільової функції містить лише перемінні першого кроку, тому що не конкретизовані варіанти рішень (або дій) у випадку, коли обсяг продукції, що випускається, перевищує обсяг попиту. Врахуємо тепер уже відомі обмеження на обсяг наявного лісу, а також умови ненегативності х_j:

(наявний у запасі ліс), (9.31)

. (9.32)

Нарешті, необхідно накласти обмеження на обсяг виробленої продукції, оскільки в супротивному випадку модель, орієнтована на максимізацію очікуваного прибутку, мабуть, приведе до значень х₁ та х₂, що перевищують рівні попиту. Допустимо далі, що президент фірми ставить за умову, щоб усі продукти і, що випускаються фірмою, були повністю реалізовані в обсязі з імовірністю, не меншою ніж .

Математично ця умова записується у такий спосіб:

(попит на пиломатеріали), (9.33)

(попит на фанеру). (9.34)

Обмеження (9.33) та (9.34) називаються імовірнісними, оскільки вони виражені через імовірності можливих наслідків. Умови (9.33) та (9.34) еквівалентні наступним звичайним лінійним нерівностям:

[детерміністський еквівалент співвідношення (9.33)], (9.35)

[детерміністський еквівалент співвідношення (9.34)]. (9.36)

Іншими словами, лінійна модель, що складається з цільової функції (9.30) та обмежень (9.31), (9.32) і детерміністських еквівалентів обмежень (9.33), (9.34), дозволяє одержати оптимальне рішення сформульованої вище задачі з імовірнісними обмеженнями.

Метод рішення. Відштовхуючись від вищенаведеного приклада, дамо загальний опис методу рішення для двокрокової моделі з імовірнісними обмеженнями. Нехай є перемінними, значення яких вибираються на першому кроці. (Перемінні другого кроку в явному вигляді не вказуємо). Допустимо, що всі коефіцієнти задані. Нарешті, припустимо, що випадкові події не залежать від того, які значення приймають перемінні першого кроку. Рішення моделі з імовірнісними обмеженнями зводиться до знаходження значень х_j у наступній задачі:

Максимізувати (9.37)

при обмеженнях (перший крок), (9.38)

(імовірнісні обмеження), (9.39)

для всіх значень j. (9.40)

Співвідношення (9.39) інтерпретується в такий спосіб: безумовна імовірність того, що виконується нерівність , не може бути менше (де задовольняє умові ).

У припущенні, що існують такі значення , що одночасно задовольняють всім умовам (9.38) – (9.40), рішення сформульованої задачі може бути отримане в результаті рішення звичайної задачі лінійного програмування, цільова функція якої має вигляд (9.37), а в систему обмежень поряд зі співвідношеннями (9.38) та (9.40) входить детерміністський еквівалент імовірнісних обмежень (9.39), а саме умова

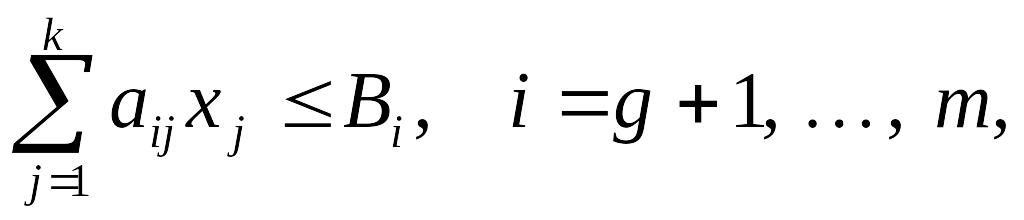(9.41)

де – граничне значення , що задовольняє умові

(9.42)

або (що те ж саме)

(9.43)

Обговорення результатів. Порівняємо тепер метод імовірнісних обмежень з викладеним раніше методом, заснованим на використанні двокрокової моделі. Модель з імовірнісними обмеженнями має дві позитивні якості. По-перше, вона зводиться до еквівалентної задачі лінійного програмування, що має ту ж розмірність і таку ж структуру, що й детерміністський аналог вихідної моделі. По-друге, щодо випадкових величин потрібно знати тільки значення констант , що визначають відповідні безумовні розподіли імовірностей. У силу зазначених властивостей моделі з імовірнісними обмеженнями вигідно відрізняються від моделей, розглянутих у попередньому розділі, коли при відображенні стохастичної задачі на звичайну задачу лінійного програмування розмірність моделі сильно зростає і, крім того, приходиться припускати, що число можливих станів Q обмежено. Основний недолік моделей імовірнісними обмеженнями полягає в тому, що економічний наслідок „порушення” того або іншого обмеження може бути оцінено лише опосередковано.

іншими словами, у більшості випадків визначення чисельних значень , що правильно описують аналізовану ситуацію, повинне бути складовою частиною оптимізаційного процесу. Необхідно також відзначити, що оптимальне рішення, отримане методом імовірнісних обмежень, може відрізнятися від оптимального рішення, знайденого за допомогою двокрокової моделі.