4.4. Рівноважний розподіл вільних носіїв заряду за швидкостями

Робота твердотільних електронних пристроїв ґрунтується на явищах електропровідності, надпровідності та інших, пов’язаних з особливостями руху вільних носіїв заряду у зовнішніх полях. Метою даного розділу є ознайомлення з сучасними уявленнями про природу названих явищ. Це можна зробити на основі викладеної у попередніх розділах інформації про будову енергетичного спектра фононів і електронів, а також статистичних закономірностях, яким підпорядковується рух цих квазічастинок. Досягнення поставленої мети можливе за умови формування уявлення про особливості руху і взаємодії квазічастинок у кристалах, зокрема розподіл електронів по швидкостях.

Для знаходження закону розподілу вільних носіїв заряду по швидкостях використаємо знайдений вище їх розподіл за енергією у досконалому напівпровіднику. Відповідно до означення функції розподілу за енергією та (4.14), кількість електронів, що володіють енергією в інтервалі (ε, ε + dε) у зоні провідності, становить величину

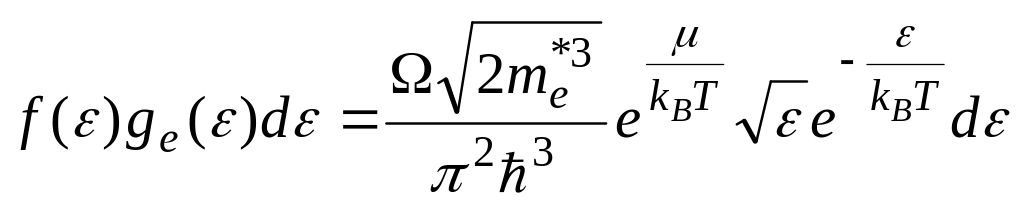. (4.30)

Вважаючи, що повна енергія електрона провідності ε = m_e^*υ²/2, з (4.30) отримується концентрація електронів, швидкість руху яких належить інтервалу (υ, υ + dυ):

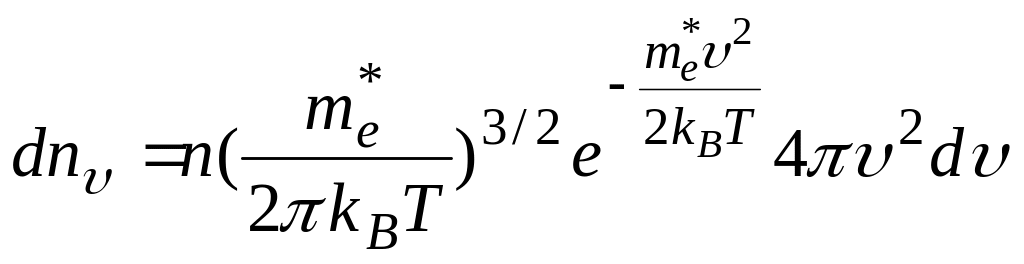. (4.31)

Тут n – їх рівноважна концентрація, що визначається формулою (4.15). Співвідношення (4.31) являє собою розподіл електронів провідності у напівпровіднику за значеннями їх швидкостей з щільністю розподілу Максвелла

. (4.32)

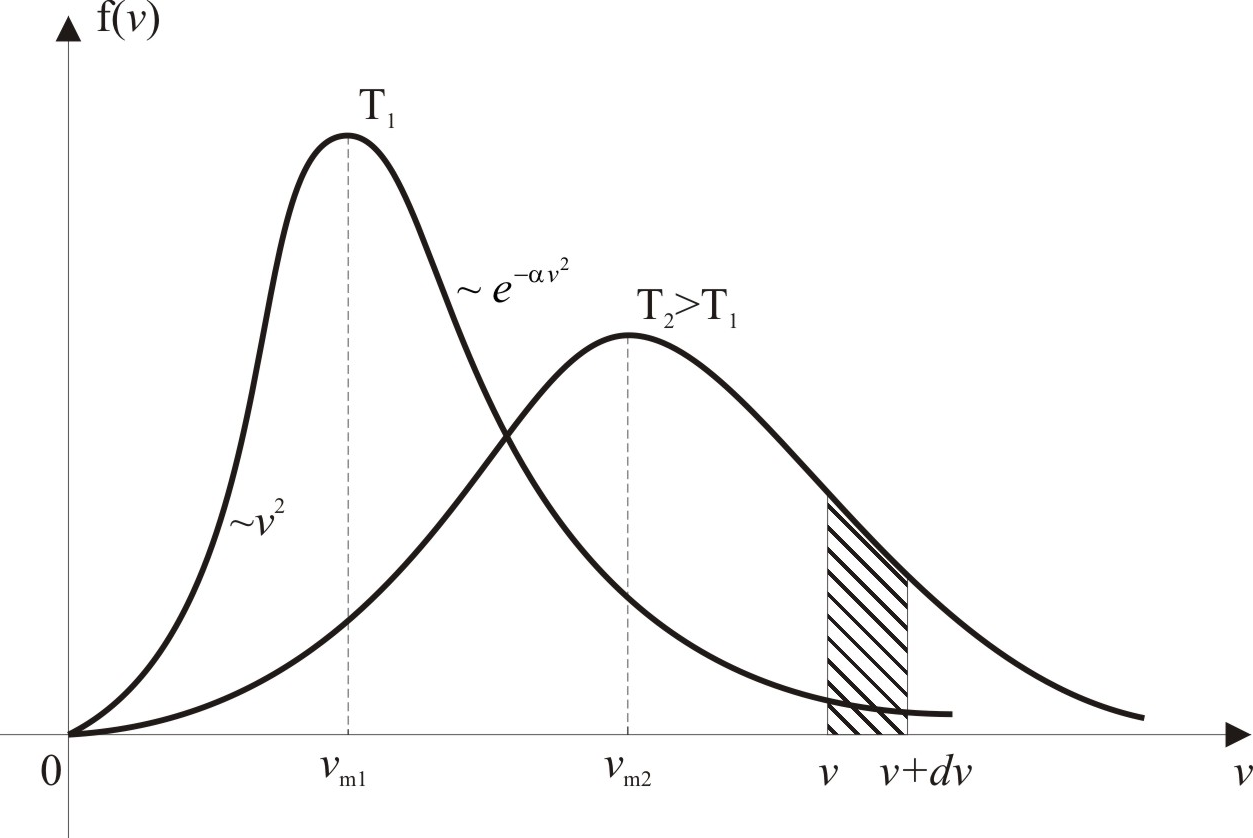
Як видно, швидкість руху електронів провідності може набувати довільного значення, проте з різною ймовірністю. Найімовірніша

Рис. 4.7. Щільність розподілу електронів провідності невиродженого напівпровідника за швидкостями (площа заштрихованої смуги дорівнює ймовірності попадання швидкості електрона у інтервал (υ, υ + dυ)

та середньоквадратична

швидкості теплового руху визначаються ефективною масою електрона, що є характеристикою системи, і температурою кристалу (зростає пропорційно до T^1/2 при її збільшенні). Оцінка, виконана за умови m_e^* = m₀ при T = 300 K свідчить, що швидкість руху електрона у напівпровіднику становить величину того ж порядку, що й швидкість вільних електронів у металах, – 10⁶ м/с.

При швидкостях, значно менших від υ_m, функція (4.32) зростає, пропорційно до υ², а при υ >> υ_m – експоненціально спадає (рис. 4.7).

Відповідно, відстань між сусідніми дозволеними значеннями однойменної компоненти його швидкості дорівнює h/(m_e^*L_i), так що деякій виділеній множині швидкостей {(υ_x, υ_x + dυ_x), (υ_y, υ_y + dυ_y), (υ_z, υ_z + dυ_z)} відповідає 2Ωdυ_xdυ_ydυ_z/(h/m_e^*)³ станів (з урахуванням їх спінового виродження). Беручи до уваги, що заповнення станів невиродженого електронного газу підпорядковується розподілу Больцмана з щільністю

,

знаходимо концентрацію електронів, що володіють швидкостями з вказаної області значень

.

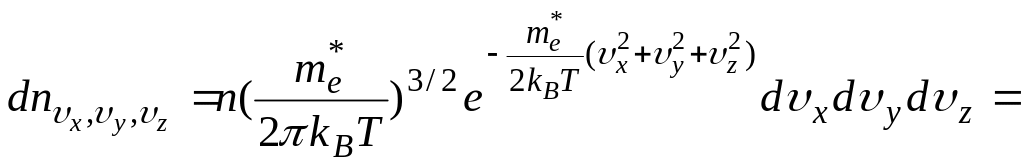
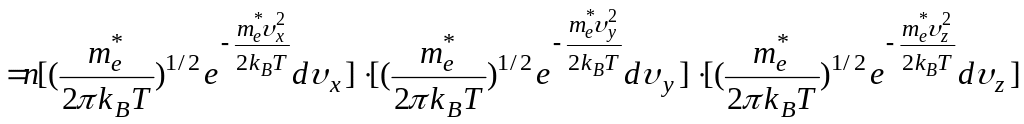Компоненти вектора швидкості електрона провідності – незалежні випадкові величини, тому кожний з виразів у прямокутних дужках являє собою ймовірність попадання υ_i у інтервал (υ_i, υ_i + dυ_i). Це означає, що функція

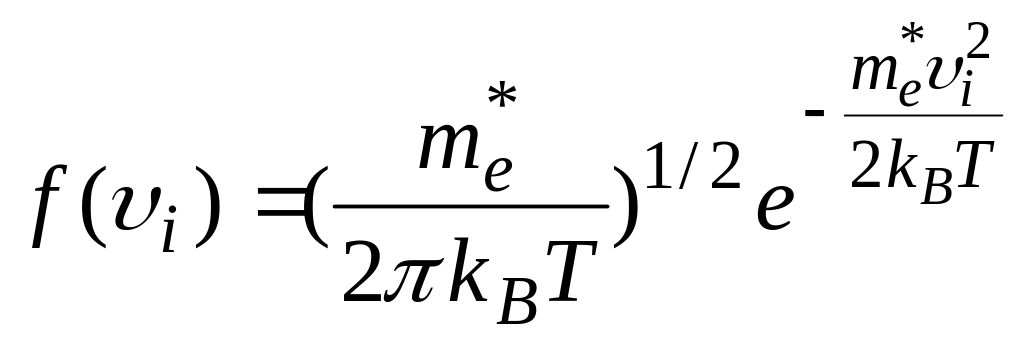(4.33)

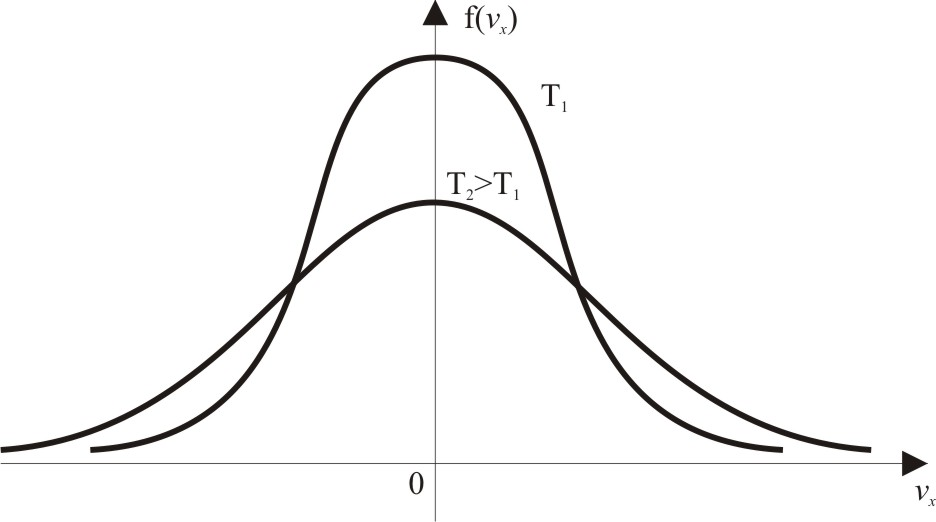
є щільністю розподілу електронів провідності невиродженого напівпровідника за і-ою компонентою вектора швидкості (i= x, y, z); її графік – гауссова крива, – схематично поданий на рис. 4.8.

Рис. 4.8. Щільність розподілу електронів провідності невиродженого напівпровідника за значеннями проекції швидкості υx

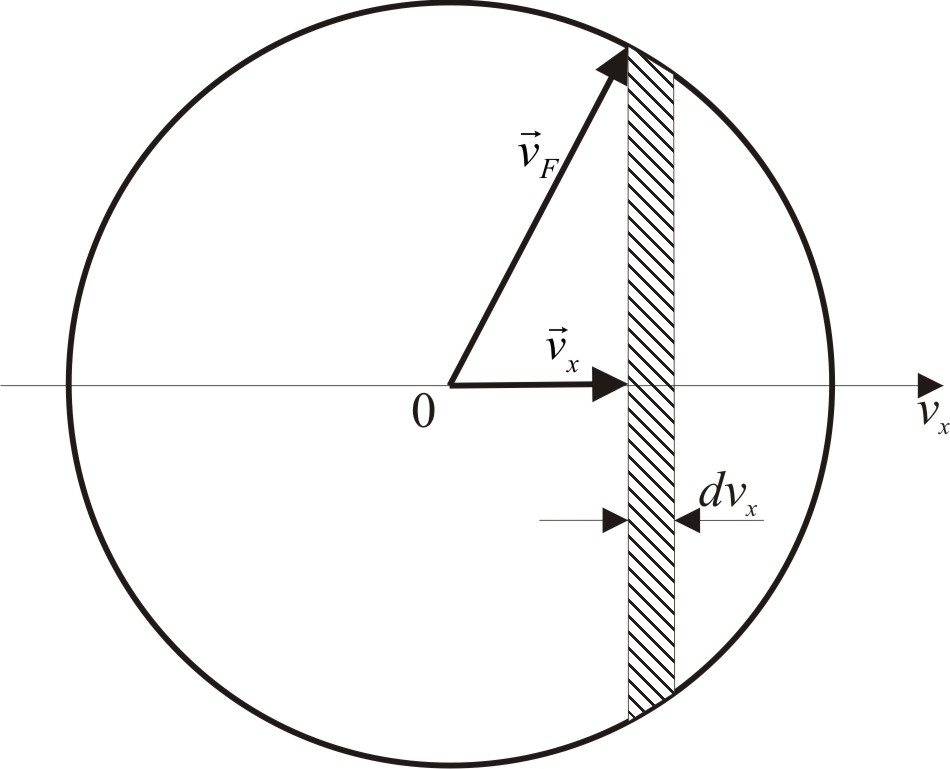
Рис. 4.9.

У випадку провідників електронний газ вироджений і при T =0 усі стани аж до рівня Фермі повністю заповнені, отже щільність розподілу електронів за швидкостями дорівнює густині станів

, (4.34)

де Ω_F = 4πυ_F³/3 – об’єм сфери Фермі радіуса υ_F.

За умови υ_x < υ_F сфера Фермі відтинає від множини точок, що містяться між площинами υ_x = const i υ_x + dυ_x = const простору зміни швидкостей область (рис. 4.9), об’єм якої при малих значеннях dυ_x становить величину π(υ_F² - υ_x²)dυ_x. Відношення цієї величини до об’єму сфери Фермі є ймовірністю того, що швидкість руху електронів вздовж вісі Ox лежить у інтервалі (υ_x, υ_x + dυ_x), а функція

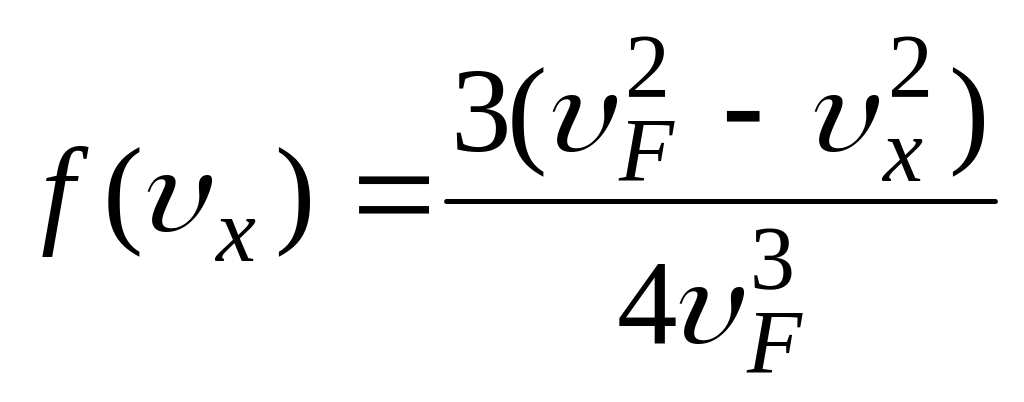– (4.35)

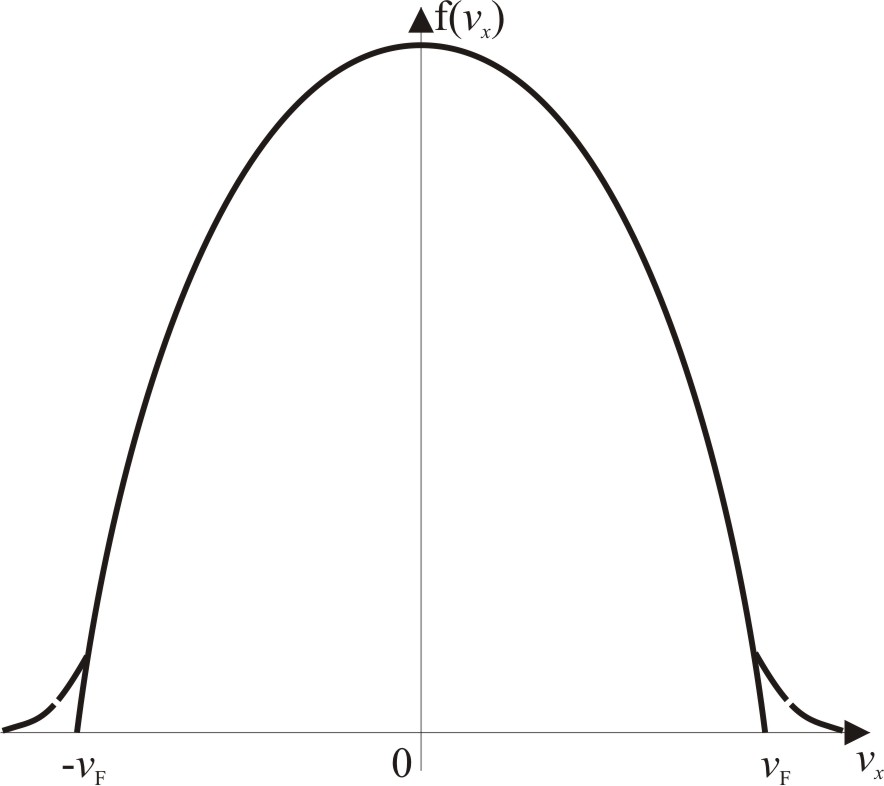
щільністю цього розподілу при T = 0; її графік наведений на рис. 4.10.

Рис. 4.10. Щільність розподілу електронів провідника за значеннями проекції швидкості υx при Т = 0 (суцільна крива) і Т ≠ 0 (пунктир)

При Т ≠ 0 має місце розмиття розподілу Фермі поблизу значень υ_x ± υ_F, що відобразиться на спотворенні параболи (4.35) в околі цих точок (пунктир на рис. 4.10).

З наведеного вище видно, що розподіл електронів за проекціями швидкостей їх теплового руху як у провідниках, так і у напівпровідниках – симетричний: f(-υ_x) = f(υ_x). Тому у стані термодинамічної рівноваги електронної системи середня швидкість їх теплового руху дорівнює нулю за будь-яких температур.

Стан термодинамічної рівноваги встановлюється і підтримується внаслідок взаємодії електронів з атомами залишками, що здійснюють коливання біля вузлів кристалічної ґратки (електрон-фононна взаємодія). Відхилення ядер від положення рівноваги при здійсненні теплових коливань викликають зміну розподілу зарядів у кристалі і, як результат – змінне електричне поле. Взаємодія електронів з цим полем і пояснює природу електрон-фононної взаємодії. Зміна енергії електрона в результаті такої взаємодії відбувається квантами величини ± ħω, що трактується як поява або зникнення фонона.

В результаті вказаних процесів (їх називають розсіюванням) відбувається обмін енергією й імпульсом між квазічастинками, що сприяє вирівнюванню температури в усьому об’ємі кристалу. Зміна енергії і імпульсу електрона можлива також внаслідок їх розсіювання на дефектах ґратки, а при великих концентраціях електронів – внаслідок взаємодії між ними.