4.2. Відмінність законів розподілу у металах і напівпровідниках

Рівняння визначає поверхню k-простору, яка відокремлює повністю зайняті (при Т = 0) одноелектронні стани від незаповнених. У наближенні квадратичного закону дисперсії це – сфера, радіуса і об’єму (сфера Фермі).

На кожний одноелектронний стан припадає елементарний об’єм (2π)³/Ω, так що їх кількість під сферою Фермі . Ці стани заповнені електронами (по два на кожному рівні), концентрація яких у кристалі-провіднику визначається енергією Фермі

(4.10)

і не залежить від температури. У металах ця величина набуває значень 10²⁵ ... 10²⁶ м^-3.

З (4.10) одержується формула для оцінки величини енергії Фермі у провідниках

. (4.11)

Вважаючи n = 5∙10²⁵ м^-3, а m_e^* рівною масі спокою вільного електрона, отримуємо E_F ≈ 5 еВ. Тоді середня енергія електрона провідності у металах

≈ 3 еВ,

а середня швидкість руху вільних електронів у металах ≈ 10⁶ м/c.

Одержані значення енергій є надзвичайно великим для мікрочастинки. Для того, щоби молекули ідеального газу володіли такою енергією, його необхідно нагріти до температури близько 25000 К. Це означає, що в області нормальних температур у металах рівність (4.9) виконується з ймовірністю, практично рівною одиниці (закон розподілу у такому випадку називають виродженим). З цієї причини електронний газ у металах також називають виродженим.

Підвищення температури провідника приводить до зміни розподілу електронів за енергією – відбувається їх перехід на незаповнені рівні вище рівня Фермі, хоча й з малою ймовірністю (f(ε) << 1 при ε > E_F). Це приводить до того, що хімічний потенціал системи електронів у провіднику стає залежним від температури. З умови незмінності кількості електронів провідності можна отримати наближений вираз, що описує температурну залежність хімічного потенціалу

, (4.12)

де E_F визначається виразом (4.11). Як видно з (4.12), зростання температури приводить до зменшення хімічного потенціалу провідника, проте, внаслідок великих значень E_F такі зменшення несуттєві – навіть при кімнатних температурах μ(Т)/μ(0) ≈ 0,9999.

У напівпровіднику функція розподілу електронів провідності експоненціально спадає при збільшенні енергії стану ε (якщо відлік енергії проводиться від дна зони провідності, то μ < 0), так що практично для усіх рівнів зони провідності за звичайних умов виконується умова невиродженості

. (4.13)

З цієї причини електронний газ у напівпровіднику, а іноді і сам кристал, називають невиродженим.

Повна функція розподілу невиродженого електронного газу

(4.14)

має немонотонну залежність від ε: в області дна зони провідності вона зростає пропорційно до , а при великих значеннях енергії – спадає пропорційно до (рис. 4.3). Це дозволяє обчислити концентрацію електронів як

,

що після інтегрування набуває вигляду

, (4.15)

де N_c – величина, яку називають ефективною кількістю станів зони провідності.

Рис. 4.3. Характер енергетичної залежності функції f(ε)ge(ε)

З (4.15) видно, що концентрація електронів провідності у напівпровіднику залежить від сорту кристалу (ним визначається значення хімічного потенціалу) та його температури – зростає при її збільшенні.

Ймовірність того, що одноелектронний стан з енергією ε незаселений, визначається функцією

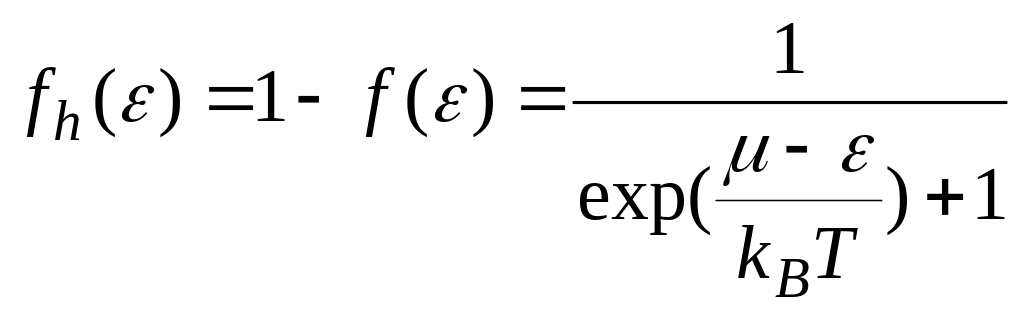, (4.16)

яку слід вважати функцією розподілу дірок. Очевидно, для глибоких рівнів валентної зони також виконується умова невиродженості закону розподілу дірок (f_h(ε) << 1), а їх концентрація

, (4.17)

де N_v – величина, яку називають ефективною кількістю станів валентної зони. Як і у випадку електронів, концентрація дірок визначається характеристиками напівпровідника (μ, E_g) та його температурою T.

Формули (4.15, 17) дозволяють встановити значення ширини забороненої зони та енергії Фермі електронного газу у досконалому напівпровіднику, а також залежність концентрації вільних носіїв заряду від E_g. Дійсно, вільні носії заряду (електрони і дірки) з’являються в ньому парами, а тому n_i = p_i (індекс і означає, що розглядається властива провідність напівпровідника). Тоді розглядаючи (4.15) і (4.17) як систему рівнянь відносно концентрацій, одержимо

– (4.18)

концентрація вільних носіїв у досконалому напівпровіднику визначається його типом (через характеристики кристалу – ширину забороненої зони, ефективні маси електрона і дірки) та температурою. Зазначимо, що формула (4.18) одержана з використанням закону розподілу Фермі-Дірака, який виконується за умови термодинамічної рівноваги в системі електронів. З цієї причини вільні носії заряду, що з’являються завдяки тепловому збудженню системи електронів у напівпровіднику, та їх концентрації, визначені формулою (4.18), називаються рівноважними. Оскільки при малих температурах множник перед експонентою в (4.18) залежить від Т слабше, ніж експонента, то можна вважати, що рівноважна концентрація електронів і дірок у досконалому напівпровіднику залежить від температури за законом

, (4.19)

де А – постійна величина.

Прирівнявши праві частини (4.15) і (4.17), одержуємо рівняння для знаходження хімічного потенціалу, звідки

, (4.20)

а E_F = μ(0) = – E_g/2 (рівень Фермі електронів у досконалому напівпровіднику відповідає середині забороненої зони).

З (4.20) видно також, що у випадку m_e^* < m_h^*, що має місце у більшості випадків, хімічний потенціал електронної системи досконалого напівпровідника зростає при його нагріванні пропорційно до абсолютної температури, а при m_e^* > m_h^* – зменшується.