6.3.2 Некоторые сведения о других методах решения жестких систем
Разностные методы (6.22) для решения жестких систем на практике используются в виде методов Гира (неявный разностный метод) и метода матричной экспоненты(метод Ракитского).
6.3.2.1 Методы Гира
Это
частный случай методов (6.22), когда
коэффициент
,
.
Запишем числовые коэффициенты, которые
определяются из условия p-го
порядка точности аппроксимации системы
разностными методами
-
;
;
(6.26)
где l=2,...,p.
Решив систему линейных уравнений (6.26) с учетом предыдущих условий, получаем все нужные коэффициенты.
Трехшаговый метод Гира (частный случай методов (6.22) с учетом условий (6.26)) имеет вид
-
.(6.27)
При m=4, получаем четырехшаговый метод Гира
-
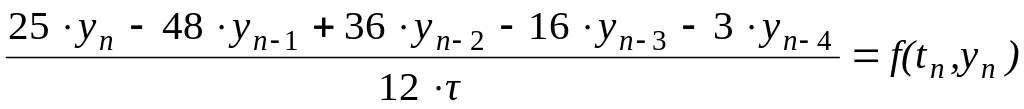.(6.28)
Запишем систему (6.26) в виде
-
.(6.29)
Решив (6.29) для
каждого случая можем найти коэффициенты
,
к=1,2,…,т.
6.3.2.2 Метод Ракитского(матричной экспоненты) решения систем оду
-
,
(6.30)
где:
;
;
А-матрица
размерности n*n.
Допустим, что матрица А - постоянная, т.е. ее элементы не зависят от времени. Система (6.30)–однородная, с постоянными коэффициентами. Запишем аналитическое решение (6.30)
-
,(6.31)
где
-матричная
экспонента и
-
+….(6.32)
Пусть необходимо (6.30) проинтегрировать при значениях t=, 2, 3,….
Если точно знать
матрицу
,
то точное решение в указанных точках
можно получить по формуле (6.31), т.е.
решение можно записать
……………..…
Таким образом, задача сводится к тому, чтобы достаточно точно знать матрицу . На практике поступают следующим образом: при больших рядом Тейлора нельзя воспользоваться в связи с его бесконечностью, т.е. для удовлетворительной точности пришлось бы взять много членов ряда, что трудно. Поэтому поступают так: отрезок [0,] разбивают на к-частей, чтобы длина h=/к удовлетворяла условию ||A*h||<0.1. Тогда запишем по схеме Горнера
.
Каждый столбец
матрицы
-
вычисляют по формуле
,
где
-
вектор столбец, в i-ой
строке которого 1, а в остальных - нули.
Если эта матрица найдена, то решение находится по (6.31).
Для исследования разностных методов при решении жестких систем рассматривают модельное уравнение
-
,(6.33)
где -произвольное комплексное число.
Для того, чтобы уравнение (6.33) моделировало исходную систему (6.30) его нужно рассматривать при таких значениях , которые являются собственными числами матрицы А. Многошаговые разностные методы (6.31) имеют вид
-
,(6.34)
где: n=m, m+1…; .
Если решение
уравнения (6.34) искать в виде
,
то для нахождения числа q
получим характеристическое уравнение
вида
.
Для устойчивости
метода достаточно выполнения условия
корней
.
В случае жестких систем используются
более узкие определения устойчивости.
Предварительные сведения. Областью устойчивости разностных методов называется множество всех точек комплексной плоскости *, для которых разностный метод применительно к уравнению (6.33) устойчив.
Определение 1. Разностный метод называется А-устойчивым, если область его устойчивости содержит левую полуплоскость комплексной полуплоскости, т.е. Re<0.
Замечание. Решение модельного уравнения (6.33) асимптотически устойчиво при значениях Re<0, поэтому сущность А-устойчивого метода заключается в том, что А-устойчивый разностный метод является абсолютно устойчивым, если устойчиво решение исходного дифференциального уравнения.
Так как класс А-устойчивых методов узок, то пользуются А()-устойчивым методом.
Определение 2. Разностный метод (6.31) называется А()-устойчивым, если область его устойчивости содержит угол меньший , т.е. |arg(-)|<, где .Исходя из этого определяется, что при А() устойчивость совпадает с определением А-устойчивого метода.