
2.1.4. Чисельні характеристики
середнього арифметичного
однаково розподілених
взаємно незалежних випадкових величин
Розглянемо n
взаємно незалежних дискретних випадкових
величин
![]() ,
які мають однакові закони розподілу
ймовірностей. Тоді їх чисельні
характеристики (математичне сподівання,
дисперсія і середнє квадратичне
відхилення) також однакові, тобто
,
які мають однакові закони розподілу
ймовірностей. Тоді їх чисельні
характеристики (математичне сподівання,
дисперсія і середнє квадратичне
відхилення) також однакові, тобто
![]()
![]()
![]()
![]() .
.
Нехай
![]() – середнє арифметичне описаних випадкових
величин, тобто
– середнє арифметичне описаних випадкових
величин, тобто
![]() .
.
Виникає
питання: який зв’язок між чисельними
характеристиками випадкової величини
і випадкових величин
![]()
Відповідь на це питання дає таке твердження: чисельні характеристики (математичне сподівання, дисперсія, середнє квадратичне відхилення) середнього арифметичного n взаємно незалежних і однаково розподілених дискретних випадкових величин виражаються такими рівностями:
![]()
![]() , (2.10)
, (2.10)
![]() .
.
Рівності (2.10) випливають з означень відповідних числових характеристик та їх властивостей:
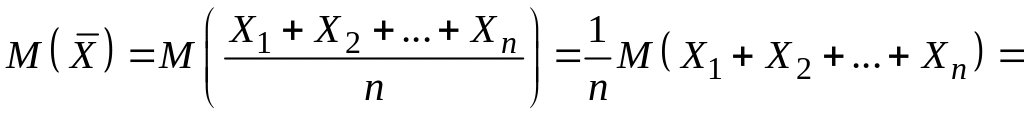
![]() ;
;
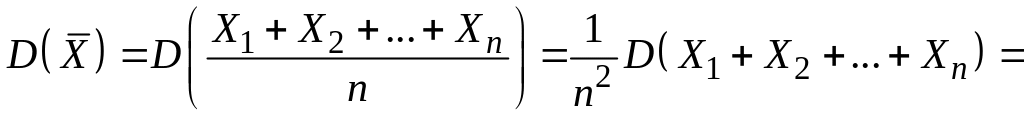
![]() ;
;
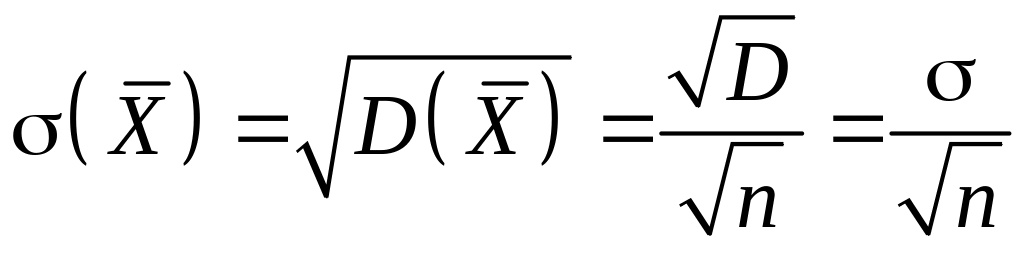 .
.
Сформульоване твердження має важливе значення для практики.
Для
встановлення певної
ознаки даної величини проводять кілька
вимірювань, результати яких є
випадковими величинами
![]() ,
бо вони залежать від багатьох випадкових
факторів. Ці величини мають однаковий
розподіл і є взаємно незалежними. Із
наведеного твердження випливає, що за
характеристику досліджуваної ознаки
доцільно обрати середнє арифметичне
одержаних результатів вимірювань
,
бо вони залежать від багатьох випадкових
факторів. Ці величини мають однаковий
розподіл і є взаємно незалежними. Із
наведеного твердження випливає, що за
характеристику досліджуваної ознаки
доцільно обрати середнє арифметичне
одержаних результатів вимірювань
![]() ,
оскільки розсіювання їх середнього
арифметичного є менше, ніж розсіювання
кожного результату вимірювання, і
воно зменшується при
,
оскільки розсіювання їх середнього
арифметичного є менше, ніж розсіювання
кожного результату вимірювання, і
воно зменшується при
![]() .
Іншими словами, значення середнього
арифметичного
результатів вимірювань ознаки випадкової
величини є надійнішим і ближчим до
істинної характеристики цієї ознаки,
ніж окремий результат.
.
Іншими словами, значення середнього
арифметичного
результатів вимірювань ознаки випадкової
величини є надійнішим і ближчим до
істинної характеристики цієї ознаки,
ніж окремий результат.
Рекомендована література: [1, с. 93–113; 2, с. 40–46, 59–68; 5, с. 64–99; 7, с. 75–77, 213–225; 8, с. 63–183].
Завдання для самоконтролю
Основні поняття, означення і відношення.
Замість крапок запишіть таке продовження (доповнення) тексту словами або формулами, щоб у результаті отримати правильне означення або твердження.
Величина називається випадковою, якщо …
Випадкова величина називається одновимірною, якщо …, і n-вимірною, якщо …
Випадкова величина називається дискретною, якщо …
Закон розподілу дискретної випадкової величини – це …
Закон розподілу дискретної випадкової величини називається біномним, якщо …
Розподілом Пуассона дискретної випадкової величини називається …
Математичне сподівання дискретної випадкової величини – це …
Математичне сподівання дискретної випадкової величини має такий імовірнісний зміст: …
Якщо Х і Y – дискретні випадкові величини, то М(Х + Y) = … і М(Х – Y) = …
Якщо Х і Y – незалежні дискретні випадкові величини, то М(Х · Y) = …
Якщо С = const і Х – дискретна випадкова величина, то М(С) = … і М(С · Х) = …
Якщо випадкова величина Х – число появ події А в n випробуваннях за схемою Бернуллі і р = Р(А) – імовірність появи А в одному випробуванні, то М(Х) = …
Відхиленням дискретної випадкової величини Х від її математичного сподівання називається …
Математичне сподівання відхилення дискретної випадкової величини Х від її математичного сподівання М(Х) дорівнює …
Дисперсією D(X) дискретної випадкової величини Х називається … , і вона обчислюється за формулами: …
Дисперсія дискретної випадкової величини має такий імовірнісний зміст: …
Якщо Х і Y – незалежні дискретні випадкові величини, то D(X + Y) = … і D(X – Y) = …
Якщо С = сonst і Х – дискретна випадкова величина, то D(C) = … і D(C · X) = …
Якщо випадкова величина Х – число появ події А в n випробуваннях за схемою Бернуллі і р = Р(А) – імовірність появи події А в окремому випробуванні, то D(X) = …
Середнім квадратичним відхиленням дискретної випадкової величини Х називається …
Середнє квадратичне відхилення дискретної випадкової величини має такий імовірнісний зміст: …
Середнє квадратичне відхилення суми кількох взаємно незалежних випадкових величин
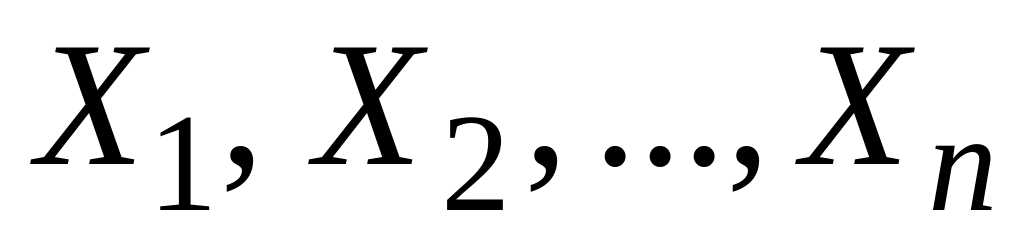 дорівнює …
дорівнює …Якщо випадкова величина Х – число появ події А в n випробуваннях за схемою Бернуллі і р = Р(А) – імовірність появи події А в одному випробуванні, то D(Х) = …
Початковим моментом s-го порядку дискретної випадкової величини Х називається …
Центральним моментом s-го порядку дискретної випадкової величини називається …
Асиметрія дискретної випадкової величини – це …
Ексцес дискретної випадкової величини – це…
Якщо
 – взаємно незалежні дискретні випадкові
величини, а
– взаємно незалежні дискретні випадкові
величини, а
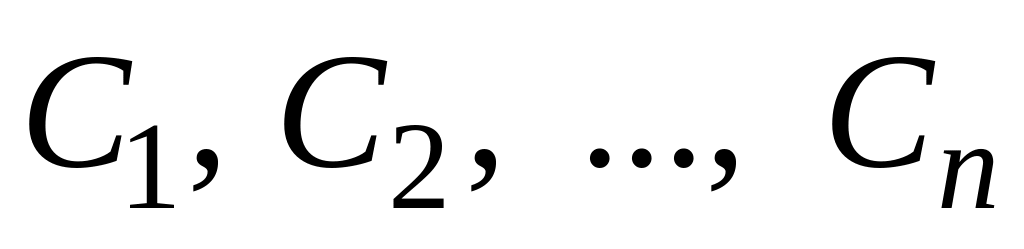 – сталі величини, то
– сталі величини, то
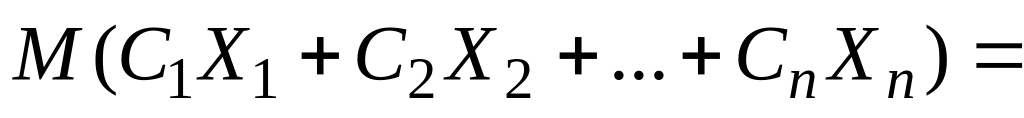 …
…Якщо
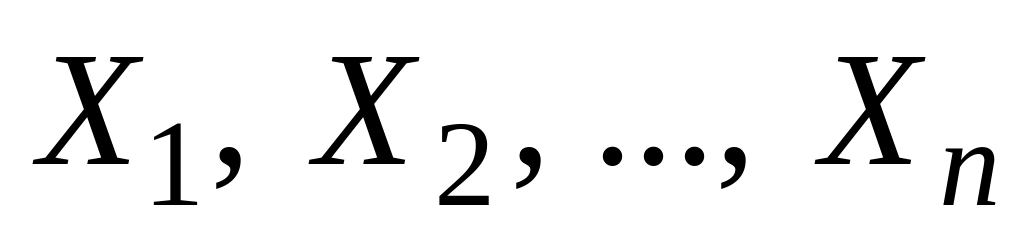 – взаємно незалежні дискретні випадкові
величини, а
– взаємно незалежні дискретні випадкові
величини, а
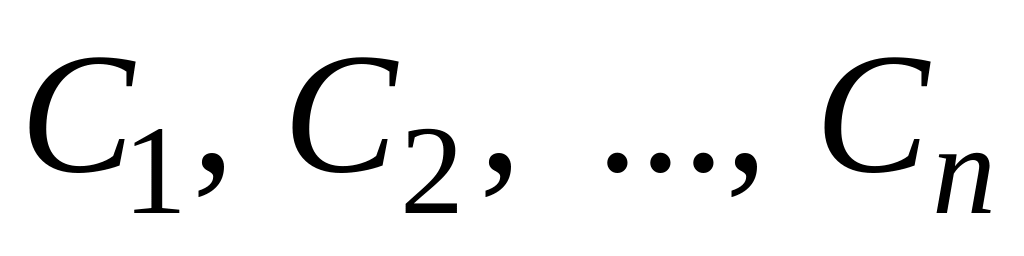 – сталі величини, то
– сталі величини, то
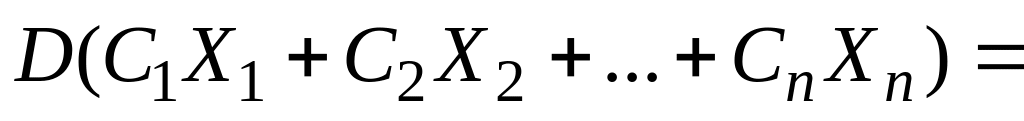 …
…Якщо
 – взаємно незалежні і однаково
розподілені дискретні випадкові
величини (
– взаємно незалежні і однаково
розподілені дискретні випадкові
величини (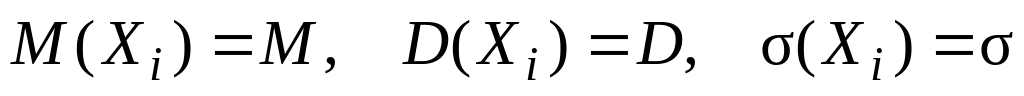 ),
а
),
а
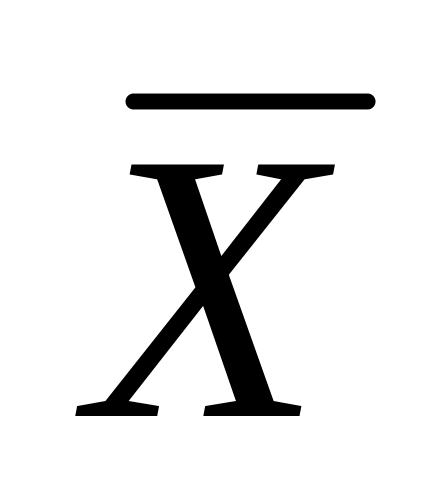 – їх середнє арифметичне, то
– їх середнє арифметичне, то
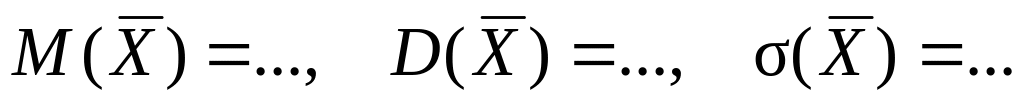
Тести
Запишіть на бланку відповідей номер завдання та коди (порядкові номери або літери), що відповідають тим варіантам відповідей, які вважаєте правильними.
Якими повинні бути числа
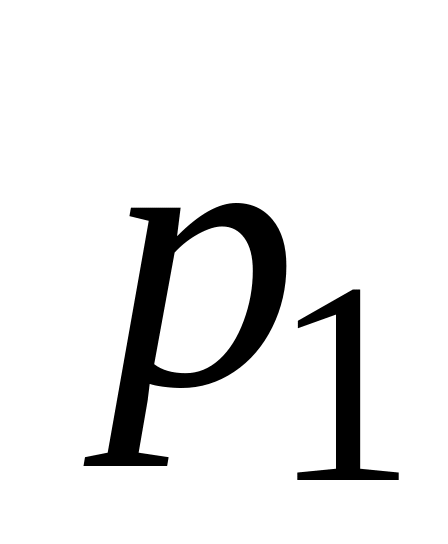 і
і
 ,
щоб таблиця:
,
щоб таблиця:
Х = хі |
х1 |
х2 |
х3 |
х4 |
х5 |
р = рі |
р1 |
0,1 |
0,3 |
0,2 |
р5 |
відображала
закон розподілу випадкової величини
Х,
якщо
![]()
Варіанти
відповідей:
1.
![]() ,
,
![]() 2.
2.
![]() ,
,
![]()
3.
![]() ,
,
![]()
2. У сейфі лежать 100 банкнот, з яких 20 – по 100 грн, 30 – по 50 грн і 50 – по 20 грн. Зі сейфа навмання виймають одну банкноту. Написати закон розподілу ймовірностей випадкової величини Х – вартості вийнятої банкноти у формі таблиці:
Х= хі |
100 |
50 |
20 |
р = рі |
|
р2 |
р3 |
Варіанти
відповідей:
1.
,
![]() ,
,
![]()
2.
,
![]() ,
,
![]()
3.
![]() ,
,
![]() ,
,
![]() .
.
3. Метеослужба міста, для прогнозування кількості снігових буранів протягом поточного року, переглянула статистичні відомості за останні 50 років і результати розподілу цих буранів подала у такій таблиці:
Кількість буранів |
0 |
1 |
2 |
3 |
4 |
5 |
Частота (к-сть років) |
2 |
4 |
8 |
12 |
14 |
10 |
Написати закон розподілу статистичних імовірностей випадкової величини Х – кількості можливих снігових буранів у поточному році і знайти ймовірність того, що поточного року їх буде не менше ніж три (подія А).
Варіанти відповідей: 1. Р(А) = 0,72. 2. Р(А) = 0,48. 3. Р(А)= 0,28.
4. Статистика свідчить, що 20% сімей мають кабельне телебачення. Навмання вибирають три сім’ї. Напишіть біномний закон розподілу випадкової величини Х – числа сімей, які мають кабельне телебачення, із трьох навмання вибраних, і обчисліть імовірність події А – не більше ніж одна сім’я із трьох навмання вибраних має кабельне телебачення.
Варіанти відповідей: 1. 0,512. 2. 0,896. 3. 0,488.
5.
Фірма відвантажила споживачеві 5 000
якісних виробів. Імовірність того, що
під час транспортування один виріб буде
пошкоджений, становить 0,0002. Випадкова
величина Х
– число пошкоджених виробів – розподілена
за біномним законом із параметрами п
= 5000, р
= 0,0002. Обчислити
перші три ймовірності цього розподілу
![]()
![]() ,
використовуючи
асимптотичну формулу Пуассона. Указати
на ймовірнісний зміст числа 2/е.
,
використовуючи
асимптотичну формулу Пуассона. Указати
на ймовірнісний зміст числа 2/е.
Варіанти відповідей. Число 2/е виражає ймовірність події:
А. Жоден виріб не буде пошкоджений.
Б. Два вироби будуть пошкоджені.
В. Не більше ніж один виріб буде пошкоджено.
6. Незалежні випадкові величини Х і Y задані такими законами розподілу:
-
Х = хі
–2
2
Y = yj
1
2
3
р = рі
…
0,7
q = qj
0,4
…
0,5
Заповніть
порожні клітинки й обчисліть
![]() .
.
Варіанти
відповідей:
1.
=
0,8. 2.
=
1,68. 3.
![]() =
2,3.
=
2,3.
7. Незалежні випадкові величини Х і Y задані такими законами розподілу:
-
Х = хі
–3
5
6
Y = yj
1
2
р = рі
0,6
…
0,2
q = qj
0,7
…
Заповніть
порожні клітинки й обчисліть D
=![]() .
.
Варіанти відповідей: 1. 0,9076. 2. 0,6976. 3. 3,698.
8. У пологовій лікарні протягом одного дня народилося п’ятеро дітей. Яке середнє число серед них хлопчиків, якщо ймовірність народження хлопчика (подія А) дорівнює 0,52?
Варіанти відповідей: 1. 2,25. 2. 2,4. 3. 2,6.
9.
Випадкова величина Х
може набувати двох можливих значень
![]() з імовірностями
з імовірностями
![]() ,
відповідно. Знайти
,
відповідно. Знайти
![]() і
і
![]() ,
якщо
,
якщо
![]() М(Х)
=
2,4,
М(Х)
=
2,4,
![]() і
і
![]() .
.
Варіанти відповідей: 1. = 2,6; = 1,6. 2. = 2,1; = 3,1.
3. = 2,6; = 3.
10. Дисперсія кожного із 36 незалежних вимірювань деякої величини дорівнює 12 см. Знайти дисперсію і середнє квадратичне відхилення середнього арифметичного результатів цих вимірювань.
Варіанти
відповідей:
1.
1/3 см і
![]() см. 2.
2
см і 2/3 см. 3.
4
см і 2 см.
см. 2.
2
см і 2/3 см. 3.
4
см і 2 см.
