1.3.1. О приближенных случайных числах

При работе на ЭВМ имеют дело с числами, длина которых ограничена разрядной сеткой ЭВМ, то есть происходит округление чисел.

Следствием округления является возможность появления зависимостей между цифрами числа  .

Физические датчики случайных величин

Физическими датчиками (генераторами) случайных величин называют физические приборы, на выходе которых формируются либо случайные напряжения, либо случайные коды.

Принцип работы многих таких устройств построен на использовании эффекта собственных шумов радиоэлектронных приборов.

Предположим, что имеется “шумящий” радиоэлектронный прибор. Напряжение на его выходе иллюстрируется следующей временной диаграммой:

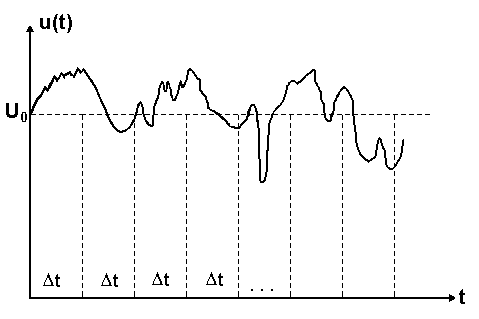
Рис. 1.1.

Зададим некоторый уровень опорного напряжения U₀ и интервал квантования по времени  t.

Можно подсчитать количество выбросов напряжения U (t) за уровень U₀ в течение каждого из интервалов времени  t. Если затем произвести суммирование по mod2 подсчитанного числа выбросов для каждого из интервалов  t, то полученная сумма будет равна 0, либо 1.

Пусть требуется сформировать r-разрядное двоичное число (на основании которого получаем к - разрядное десятичное). В этом случае для определения r разрядов первого числа ₁ , используется r интервалов  t, следующие r интервалов  t определяют число ₂ и т.д.

При этом должна быть обеспечена одинаковая вероятность появления нулей и единиц. Чтобы не проверять равенство вероятностей, используется схема стабилизации вероятностей, когда один двоичный разряд выходного числа  формируется с помощью двух интервалов  t.

В этом случае комбинация {01} принимается за 1, комбинация {10}- за 0. Комбинации {00} и {11} не рассматриваются и отбрасываются.

Достоинство физических датчиков:

1. Запас чисел практически не ограничен, т.е. вероятность повторения чисел при моделировании пренебрежимо мала.

Недостаток. Необходимо иметь специальное физическое устройство.2. С течением времени все радиоэлектронные приборы изменяют свойства, следовательно, датчики во времени работают нестабильно, поскольку у формируемой ими последовательности чисел может меняться вид закона распределения и его параметры.

3. В процессе моделирования датчик невозможно проверить, поэтому каждый его сбой будет сказываться на результатах моделирования.

О проверке физических датчиков случайных чисел

Особенностью проверки физических датчиков случайных величин является то, что проверяются не те числа, которые используются при моделировании.

Физический датчик проверяется до начала моделирования и после его окончания, в процессе моделирования проверка не производится.

Поэтому к физическим датчикам случайных величин предъявляются жесткие требования стабильности работы во времени.

Метод псевдослучайных чисел

Псевдослучайными называются такие числа, которые формируются по заранее заданному алгоритму, но обладают всеми свойствами случайных чисел.

Конкретную последовательность псевдослучайных чисел можно всесторонне проверить, а затем многократно применять.

Достоинства датчиков псевдослучайных чисел:

1. Программы формирования псевдослучайных чисел очень просты и состоят из нескольких операторов.

2. Числа формируются во времени устойчиво, в отличие от физических датчиков.

Недостатки:

1. Последовательность псевдослучайных чисел, в силу конечной длины разрядной сетки ЭВМ, всегда ограничена, т.е. начиная с некоторого числа, при моделировании неизбежно начнется повторение случайных чисел.

2. Числа формируются медленнее, чем при использовании физических датчиков.

В настоящее время это основной способ формирования случайных чисел при моделировании на ЭВМ.