4.6. Оценка точности линеаризованных решений дифференциальных уравнений движения поезда
Основной моделирующий алгоритм, вычисляющий величину межпоездного интервала, в процессе своей работы обращается к подпрограмме, которая вычисляет либо конечную скорость и время по заданной начальной скорости и пути, который надо пройти, либо конечную скорость и путь по известной начальной скорости и времени. Для определения всех этих величин подпрограмма использует решения дифференциальных уравнений, описывающих движение поезда.
Часть вышеуказанных уравнений имеет аналитическое решение, часть – не имеет и может быть решена методом Симпсона. Разработана соответствующая подпрограмма для основного моделирующего алгоритма, которая использовала решения данных дифференциальных уравнений. Однако оказалось, что время счета этой подпрограммы слишком велико, а поскольку в течение одного прогона основная программа обращается к подпрограмме много раз, то при использовании данного метода время счета сильно возрастает.
В связи с этим
было предложено использовать не точные,
а линеаризованные уравнения движения,
т.е. ускорение, вычисляемое по формуле
,
считать постоянным на каждом подучастке
(с постоянным уклоном) и вычислять
соответственно по формулам (1-2), (4), (6) п.
4.4, подставляя вместо
величину скорости в начале данного
подучастка. Таким образом, сложное
движение, описываемое вышеуказанными
дифференциальными уравнениями, заменяется
кусочно-равноускоренным движением.
Применение линеаризации существенно
снижает время счета одного прогона
модели, однако необходимо предварительно
убедиться в том, что возникающие при
этом погрешности допустимы в рамках
моделирующего алгоритма. Для этого была
разработана вторая подпрограмма, по
структуре аналогичная первой, но в
отличие от нее, использующая линеаризованные
уравнения движения. Далее при одних и
тех же исходных данных были пропущены
обе подпрограммы и найдены величины
погрешностей:
,
,
,
что и дает оценку точности решений
линеаризованных дифференциальных
уравнений движения поезда.
4.7. Результаты моделирования
4.7.1. Описание объекта моделирования и исходные данные
Для апробации математической модели функционирования двухпутного участка, определения основных параметров программы и ее возможностей эта модель была настроена на определенный объект моделирования. В качесте такого объекта был взят конкретный двухпутный ж.д. участок с автоблокировкой и диспетчерской централизацией.
Исходные данные для моделирования содержат:
- условно- постоянную (нормативно-справочную) информацию,
- переменную информацию.
Нормативно-справочная информация содержит:
1) профиль моделируемого ж.д. участка,
2) расстановку светофоров на ж.д. участке,
3) распределение вероятностей весов и длин поездов,
4) коэффициенты уравнений движения поезда,
5) нормативные правила действий машиниста при различных показаниях светофоров.
Дадим краткое описание нормативно-справочной информации.
Данный железнодорожный участок состоит из 34 блок-участков. Их длины приведены в нижеследующей таблице 4.4.
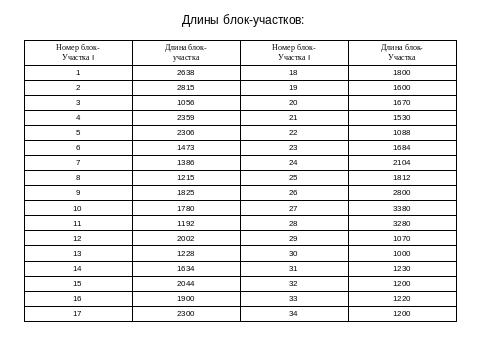
В исходных данных задается профиль пути таким образом, что каждый блок-участок делится на подучастки с различным значением уклона ( ). Если при движении, которое рассчитывается с помощью системы (2 - 7) п. 4.4, поезд проходит несколько таких подучастков, то уравнения (2 - 7) п. 4.4 решаются для каждого отдельного подучастка с разными значениями коэффициентов. Профиль ж.д. участка задается таблицей 4.5.
Задается совместное распределение весов и длин поездов на рассматриваемом учкастке. Для получения гистограммы этого распределения с 250 скоростемерных лент были сняты данные о весах и длинах поездов и обработаны в соответствии с правилами математической статистики. Полученное совместное двумерное распределение приведено в таблице 4.6.
Коэффициенты уравнений движения поезда приведены ранее. Нормативные правила действий машиниста при различных показаниях светофоров отражены в моделирующем алгоритме.
Переменная информация содержит начальное расположение поездов на участке, их длины и веса, их фазы обслуживания. Эти данные сведены в таблицу 4.7.
Таблица 4.5
Профиль пути
№ б/у |
1 подучасток |
2 подучасток |
3 подучасток |
4 подучасток |
5 подучасток |
|
Уклон, длина, км |
Уклон, длина, км |
Уклон, длина, км |
Уклон, длина, км |
Уклон, длина, км |
1 |
1,3 0,299 |
-0,2 0,75 |
1,7 0,6 |
1,7 0,989 |
|
2 |
1,7 0,611 |
-1,7 1,53 |
0,3 0,674 |
|
|
3 |
0,3 0,696 |
0 0,2 |
-0,4 0,16 |
|
|
4 |
-0,4 0,51 |
3,1 0,83 |
-0,2 0,197 |
-0,2 0,303 |
1,4 0,519 |
5 |
1,4 1,781 |
-0,2 0,525 |
|
|
|
6 |
-0,2 0,675 |
2 0,798 |
|
|
|
7 |
2 1,386 |
|
|
|
|
8 |
2 0,416 |
-0,5 0,799 |
|
|
|
9 |
-0,5 0,501 |
0,4 1,19 |
-0,5 0,134 |
|
|
10 |
-0,5 1,476 |
1,2 0,304 |
|
|
|
11 |
1,2 0,796 |
-1,1 0,396 |
|
|
|
12 |
-1,1 0,104 |
2,7 0,65 |
-2 0,75 |
1 0,2 |
-0,5 0,298 |
13 |
-0,5 0,802 |
1 0,4 |
|
|
|
14 |
0 0,3 |
-2 0,65 |
2 0,2 |
-1,3 0,484 |
|
15 |
-1,3 0,466 |
0,5 0,56 |
-2,4 2,018 |
|
|
16 |
-2,4 0,852 |
2,5 1,048 |
|
|
|
17 |
2,5 0,822 |
1,2 1,478 |
|
|
|
18 |
1,2 0,722 |
-0,4 0,3 |
1 0,778 |
|
|
19 |
1 1,152 |
-5,1 0,448 |
|
|
|
20 |
-5,1 1,67 |
|
|
|
|
21 |
-5,1 0,452 |
2,7 0,84 |
1,6 0,238 |
|
|
22 |
-1,6 0,322 |
0,9 0,765 |
|
|
|
23 |
0,9 0,685 |
-5,9 0,999 |
|
|
|
24 |
-5,9 1,263 |
-1,6 0,841 |
|
|
|
25 |
-1,6 0,259 |
0,4 0,8 |
-0,3 0,6 |
3,8 0,153 |
|
26 |
3,8 1,812 |
|
|
|
|
27 |
3,8 0,786 |
0,3 0,634 |
0,3 0,86 |
|
|
28 |
0,3 0,5 |
0,7 0,5 |
4,6 1,12 |
-2,2 0,171 |
|
29 |
-2,2 0,809 |
1,6 0,18 |
1,6 0,8 |
-3 0,27 |
|
30 |
-3 1 |
|
|
|
|
31 |
-3 0,511 |
2,1 0,609 |
-3,7 0,11 |
|
|
32 |
-3,7 0,12 |
|
|
|
|
33 |
-3,7 0,379 |
1,7 0,55 - |
0,9 0,291 |
|
|
34 |
-0,9 0,159 |
2,8 0,75 |
0 0,391 |
|
|
Таблица 4.6
Совместное распределение веса и длины поезда
\Вес Длина\ |
300- 780 |
780- 1260 |
1260- 1740 |
1740- 2220 |
2220- 2700 |
2700- 3180 |
3180- 3660 |
3660- 4140 |
4140- 4620 |
4620- 5100 |
10-46 |
0,00578 |
0,00578 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
46-82 |
0,011561 |
0 |
0,00578 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
82-118 |
0,00578 |
0 |
0 |
0,00578 |
0 |
0 |
0 |
0 |
0 |
0 |
118-154 |
0 |
0 |
0,00578 |
0 |
0 |
0,00578 |
0,017341 |
0 |
0,00578 |
0 |
154-190 |
0 |
0,0289 |
0 |
0,017341 |
0,00578 |
0,011561 |
0,00578 |
0,0231 |
0 |
0 |
190-226 |
0 |
0,03468 |
0,00578 |
0,011561 |
0,04046 |
0,0867 |
0,127168 |
0,121387 |
0,08092 |
0,01734 |
226-262 |
0 |
0 |
0,00578 |
0,00578 |
0,00578 |
0,00578 |
0,0289 |
0,04624 |
0,098265 |
0,02312 |
262-298 |
0 |
0 |
0,00578 |
0 |
0 |
0 |
0 |
0,00578 |
0,011561 |
0 |
298-334 |
0 |
0 |
0 |
0 |
0 |
0 |
0,00578 |
0 |
0 |
0 |
334-370 |
0 |
0 |
0 |
0 |
0,00578 |
0 |
0 |
0 |
0 |
0 |
Таблица 4.7.
Начальное распределение поездов на ж.д. участке
№ б/у |
Наличие «головы» поезда на блок-участке |
Фаза обслуживания |
Скорость движения |
Расстояние до конца фазы обслуживания |
Расстояние до конца блок-участка |
Длина поезда |
Вес поезда |
Показания светофора |
1 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
2 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
3 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
4 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
5 |
1 |
1 |
22,2 |
900 |
900 |
1276 |
1980 |
2 |
6 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
7 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
8 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
9 |
1 |
1 |
22,2 |
1100 |
1100 |
623,5 |
2460 |
2 |
10 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
11 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
12 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
13 |
1 |
1 |
22,2 |
200 |
200 |
88,5 |
2460 |
2 |
14 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
15 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
16 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
17 |
1 |
1 |
22,2 |
1200 |
1200 |
1015 |
3900 |
2 |
18 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
19 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
20 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
21 |
1 |
1 |
22,2 |
100 |
100 |
1276 |
1980 |
2 |
22 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
23 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
24 |
1 |
1 |
22,2 |
1300 |
1300 |
493 |
1500 |
2 |
25 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
26 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
27 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
28 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
29 |
1 |
1 |
22,2 |
1300 |
1300 |
493 |
1500 |
2 |
30 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
31 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
32 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
1 |
33 |
1 |
1 |
22,2 |
50 |
50 |
754 |
4860 |
2 |
34 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
0 |
В графе 2 поставлено: 1, если «голова» поезда находится на блок-участке,
0 в противном случае.