
- •Введение
- •Глава 1. Моделирование случайных величин
- •1.1.1. Понятия модели и моделирования
- •1.1.2. Основной цикл познания при моделировании
- •1.1.3. Математическое моделирование
- •1.1.3.1. Математическое описание сложных систем
- •1.1.3.2. Методы математического моделирования
- •1.1.3.3. Имитационное моделирование
- •1.1.3.4. Принципы построения алгоритмов имитационного моделирования
- •1.1.3.5. Характерные особенности имитационного моделирования на эвм
- •1.1.3.6. Статистическое моделирование
- •1.1.3.7. Понятие о вероятностном физическом моделировании
- •1.1.3.8. Достоинства метода имитационного моделирования на эвм
- •1.1.3.9. Недостатки метода имитационного моделирования
- •1.2. Структура имитационной модели. Технологии построения.
- •1.2.1. Этапы разработки имитационной модели
- •1.2.2. Элементы и структура имитационной модели
- •1.2.3. Технология построения и функционирования.
- •1.3. Генерирование равномерно распределенных на интервале [0,1] случайных чисел. Проверка качества генераторов случайных чисел
- •1.3.1. О приближенных случайных числах
- •Физические датчики случайных величин
- •О проверке физических датчиков случайных чисел
- •Метод псевдослучайных чисел
- •Алгоритмы получения псевдослучаных чисел
- •Алгоритмы порядка r
- •Метод возмущений
- •Генератор Лемера
- •Проверка качества формируемой последовательности псевдослучайных чисел
- •1.4. Методы генерирования случайных событий, дискретных и непрерывных случайных величин, многомерных случайных величин, усеченных случайных величин.
- •1.4.1. Моделирование дискретных случайных величин
- •1.4.2. Моделирование семейства биномиальных распределений
- •1.4.3. Моделирование непрерывных случайных величин Метод обратных функций
- •Метод суперпозиций
- •Моделирование многомерных случайных величин
- •Моделирование n-мерной точки с зависимыми координатами
- •Метод отбора
- •Применение метода отбора. Моделирование усеченных распределений
- •Метод Неймана
- •Выбор равномерно распределенных точек в сложных областях
- •1.5. Методы генерирования наиболее часто встречающихся на практике распределений.
- •1.5.1. Моделирование распределения Эрланга
- •1.5.2. Приближенное моделирование нормально распределенных случайных величин
- •1.5.3. Методы генерирования цепей и процессов Маркова.
- •1.5.4. Метод генерирования процессов Маркова с дискретным множеством состояний.
- •1.5.5. Метод генерирования процессов Маркова с дискретно-непрерывным множеством состояний.
- •Глава 2. Моделирование информационных систем железнодорожного транспорта
- •2.1. Формирование реализаций случайных потоков
- •Однородных событий.
- •2.1.1. Входящие потоки
- •2.1.2. Формирование произвольных случайных потоков однородных событий
- •2.2. Введение марковских процессов при моделировании систем массового обслуживания при произвольных распределениях основных случайных величин.
- •2.3. Моделирование однолинейной системы массового обслуживания
- •2.3.1. Распределение длины очереди
- •2.3.2. Время отклика и время ожидания
- •2.4. Моделирование многолинейной системы массового обслуживания
- •2.4.1. Моделирование многолинейной системы массового обслуживания для расчете времени ожидания
- •2.4.2. Моделирование многолинейной системы массового обслуживания для расчета распределения числа требований в системе.
- •2.5. Моделирование сетей массового обслуживания,
- •Глава 3. Оценка точности результатов моделирования
- •3.1. Постановка задачи по оценке точности результатов моделирования. Характеристики точности результатов моделирования Оценка точности результатов аналитического моделирования
- •3.1.1. Постановка задачи по оценке точности результатов
- •3.1.2. Классификация входных случайных величин
- •3.1.3. Смещение и дисперсия оценки выходного показателя
- •3.2. Оценка точности результатов имитационного
- •3.2.1. Оценка смещения
- •3.2.2. Оценка составляющей дисперсии за счет неточности входных параметров
- •3.2.3. Оценка частных производных от показателя эффективности сложной системы на ее математической модели
- •3.3. Оценка точности результатов статистического
- •Глава 4. Разработка математической модели функционирования двухпутного железнодорожного участка для определения минимального расчетного межпоездного интервала
- •4.1. Постановка задачи
- •4.1.1. Актуальность разработки модели
- •4.1.2. Постановка задачи по разработке модели.
- •4.2.2. Кусочно-непрерывный марковский процесс, описывающий функционирование двухпутного железнодорожного участка
- •4.3. Алгоритм смены состояний кусочно-непрерывного процесса, функционирования железнодорожного участка во времени
- •4.4. Уравнения движения поезда
- •4.5. Программная реализация алгоритма математической модели функционирования двухпутного ж.Д. Участка
- •4.6. Оценка точности линеаризованных решений дифференциальных уравнений движения поезда
- •4.7. Результаты моделирования
- •4.7.1. Описание объекта моделирования и исходные данные
- •4.8. Результаты моделирования для обычных грузовых поездов
- •4.9. Результаты моделирования для поездов повышенной длины и массы
- •4.10. Результаты расчета точности решений линеаризованных уравнений движения поезда
- •Глава 5. Задачи по дисциплине «Моделирование систем» для студентов 4 курса по кафедре «асу» по направлениям
- •Оглавление
- •Глава 1
- •Глава 2. Моделирование информационных систем
- •2.3. Моделирование однолинейной системы массового обслуживания………………………………………………………………...52
- •2.4. Моделирование многолинейной системы массового обслуживания..55
- •Глава 3. Оценка точности результатов моделирования…………………...63
- •Глава 4. Разработка математической модели функционирования
- •Глава 5. Задачи по дисциплине «Моделирование систем»
2.4.2. Моделирование многолинейной системы массового обслуживания для расчета распределения числа требований в системе.
Рассмотрим
многолинейную систему массового
обслуживания с ожиданием с
обслуживающими приборами. Входящий
поток является рекуррентным. В начальный
момент система свободна. Требования
поступают в моменты
![]() ,
величины
=
,
величины
=
![]() независимы
в совокупности и обладают одним и тем
же законом распределения
независимы
в совокупности и обладают одним и тем
же законом распределения
![]() .
Длительности обслуживания требований
- независимые в совокупности случайные
величины
.
Длительности обслуживания требований
- независимые в совокупности случайные
величины
![]() с распределением
с распределением
![]()
![]() .
Предполагаем, что последовательности
(
)
и (
)
взаимно независимы. Обозначим через
число
требований в системе в момент
- 0,
.
Предполагаем, что последовательности
(
)
и (
)
взаимно независимы. Обозначим через
число
требований в системе в момент
- 0,
![]() - число поступивших требований в систему
до момента
и
- число поступивших требований в систему
до момента
и
![]() - число обслужившихся требований системой
до момента
.
- число обслужившихся требований системой
до момента
.
Пусть в момент
=0
= 0. Легко видеть, что здесь также
=
-
.
Всегда
![]() .
С поступлением первого требования в
момент
.
С поступлением первого требования в
момент
![]() становится больше 0. Обозначим через
становится больше 0. Обозначим через
![]() первый момент времени, когда
снова обратится в нуль. Интервал (
,
)
также называется периодом занятости
системы, периоды времени, когда
= 0, являются свободными периодами. За
свободным периодом следует период
занятости, затем снова свободный период,
затем период занятости и т.д.
первый момент времени, когда
снова обратится в нуль. Интервал (
,
)
также называется периодом занятости
системы, периоды времени, когда
= 0, являются свободными периодами. За
свободным периодом следует период
занятости, затем снова свободный период,
затем период занятости и т.д.
Построим моделирующий алгоритм на периоде занятости. Заметим, что значения процесса являются целочисленными и меняются скачками, а именно, в момент поступления требования входящего потока к прибавляется 1, в момент ухода из системы обслужившегося требования из вы-читается 1. Весь период занятости состоит из последовательно следующих один за другим периодов увеличения и периодов уменьшения .
Начинается период
занятости с периода увеличения
,
к
= 0 прибавляется 1. Реализуется время
обслуживания
![]() .
Реализуются также случайные величины
.
Реализуются также случайные величины
![]() .
Если
.
Если
![]() ,
то в счетчик длительностей интервалов
записывается пара (1,
),
где
- длина интервала, на котором
= 1, и
,
то в счетчик длительностей интервалов
записывается пара (1,
),
где
- длина интервала, на котором
= 1, и
![]() )
= 0. На этом период увеличения
заканчивается.
)
= 0. На этом период увеличения
заканчивается.
Однако далее идет
уже более сложный процесс моделирования.
Обозначим через
![]() моменты
времени, когда процесс
претерпевает скачки. Осуществим
моделирования перехода состояния
процесса
из момента времени
моменты
времени, когда процесс
претерпевает скачки. Осуществим
моделирования перехода состояния
процесса
из момента времени
![]() в
в
![]() .
Для этого введем векторный марковский
процесс
.
Для этого введем векторный марковский
процесс
![]() =
(
,
=
(
,
![]() ,
где
- время с момента
до момента поступления следующего
требования,
,
где
- время с момента
до момента поступления следующего
требования,
![]() - время с момента
до момента окончания обслуживания
требования на
- время с момента
до момента окончания обслуживания
требования на
![]() - ом канале, которое обслуживалось на
нем в момент времени
,
- ом канале, которое обслуживалось на
нем в момент времени
,
![]() .
Величина
= 0, если
- ый канал в момент времени
был свободен. Для моделирования поведения
процесса
отводим
+ 2 ячеек для хранения в них значений
компонент процесса
,
т.е.
,
.
Величина
= 0, если
- ый канал в момент времени
был свободен. Для моделирования поведения
процесса
отводим
+ 2 ячеек для хранения в них значений
компонент процесса
,
т.е.
,
![]() .
Изменения процесса
рассматриваем только в моменты времени
.
.
Изменения процесса
рассматриваем только в моменты времени
.
Пусть в момент
времени
имеем
![]() =
(
=
(![]() ,
,
![]() .
Опишем процедуру перехода к процессу
в момент времени
,
т.е. процедуру нахождения значения
процесса
в момент времени
,
а именно,
.
Опишем процедуру перехода к процессу
в момент времени
,
т.е. процедуру нахождения значения
процесса
в момент времени
,
а именно,
![]() =
(
=
(![]() ,
,
![]() Имеет место следующий алгоритм.
Имеет место следующий алгоритм.
Находим
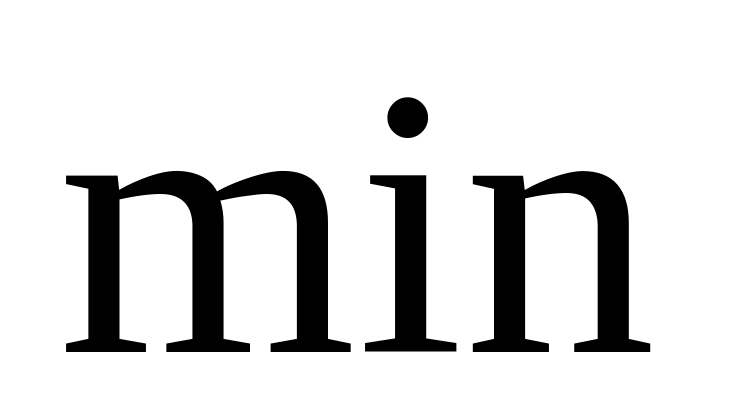 (
.
(
.Если ( =
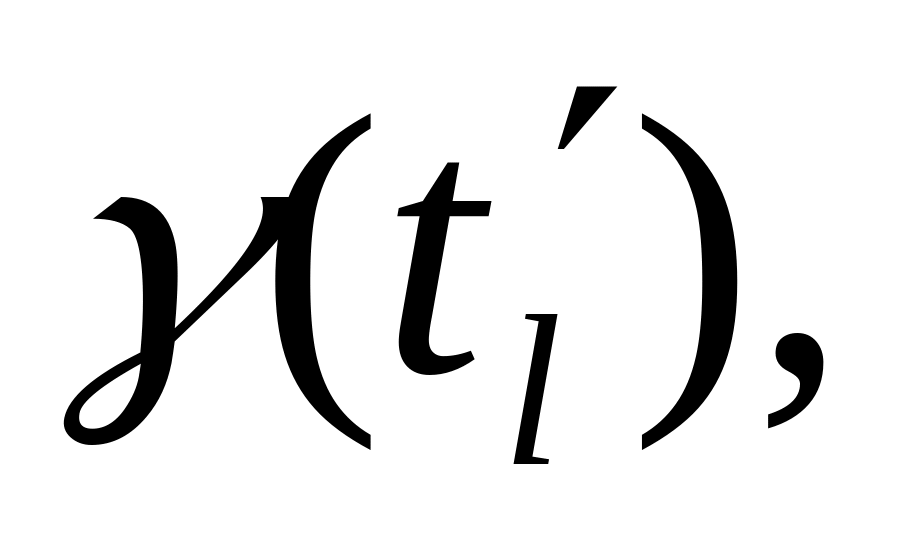 то модельное время увеличивается на
величину
в ячейку для
то модельное время увеличивается на
величину
в ячейку для
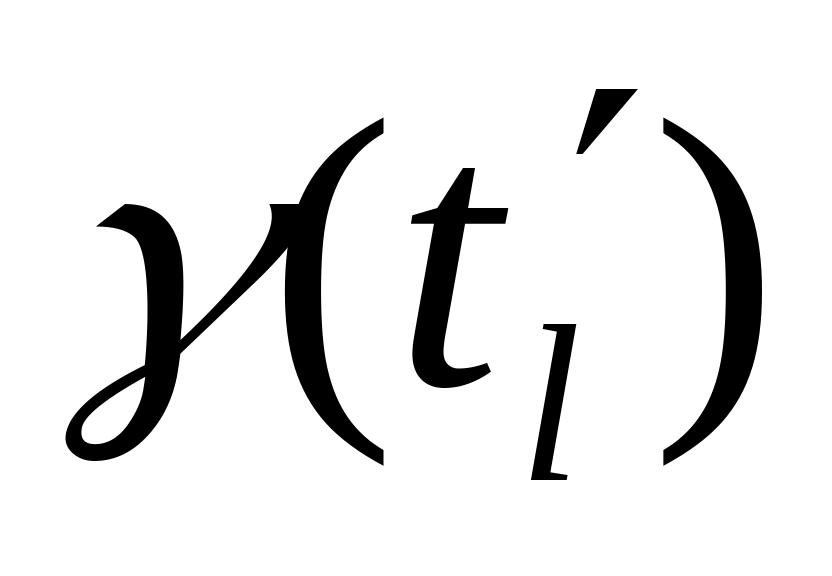 заносится величина интервала до момента
поступления следующего требования
заносится величина интервала до момента
поступления следующего требования
 ,
в ячейку для
заносится величина
+1, если все величины
,
в ячейку для
заносится величина
+1, если все величины
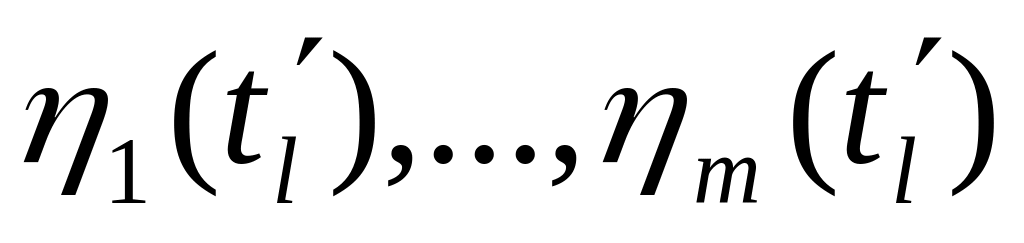 больше 0, т.е.
больше 0, т.е.
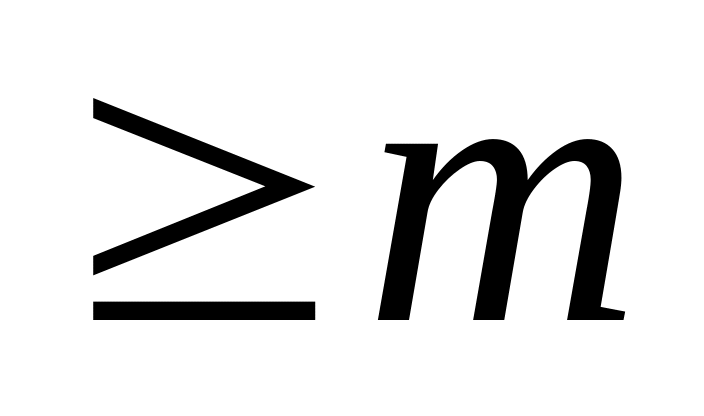 ,
то они уменьшаются на величину
.
Модельное время увеличивается на
величину
.
Таким образом,
=
(
,
будет равен (
=
+1 ,
,
то они уменьшаются на величину
.
Модельное время увеличивается на
величину
.
Таким образом,
=
(
,
будет равен (
=
+1 ,

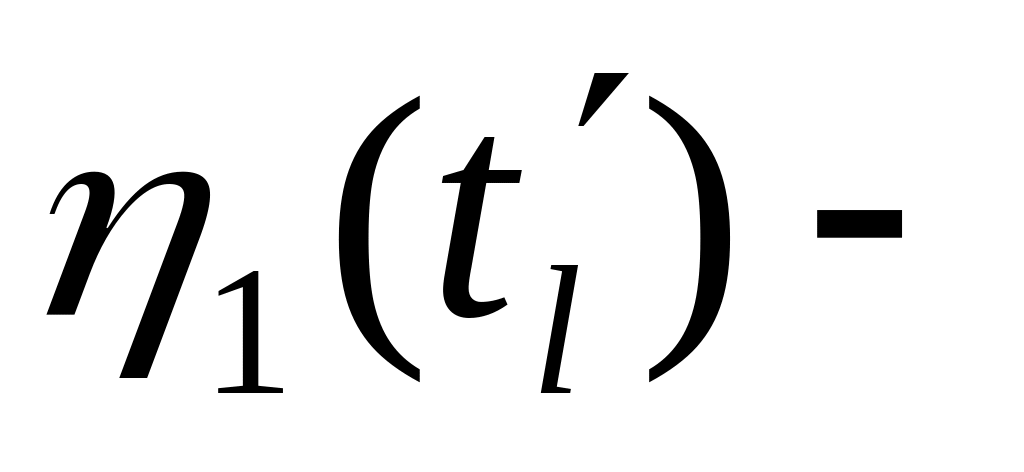 …,
…,
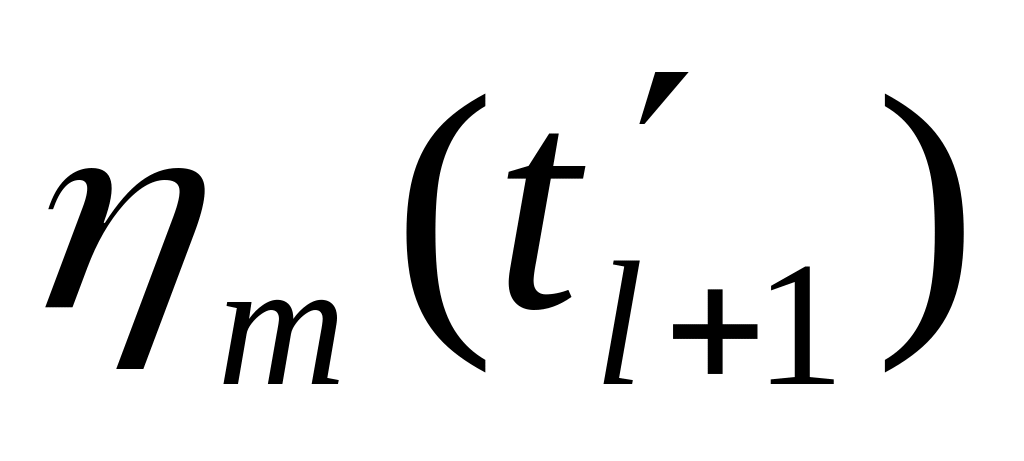 =
=
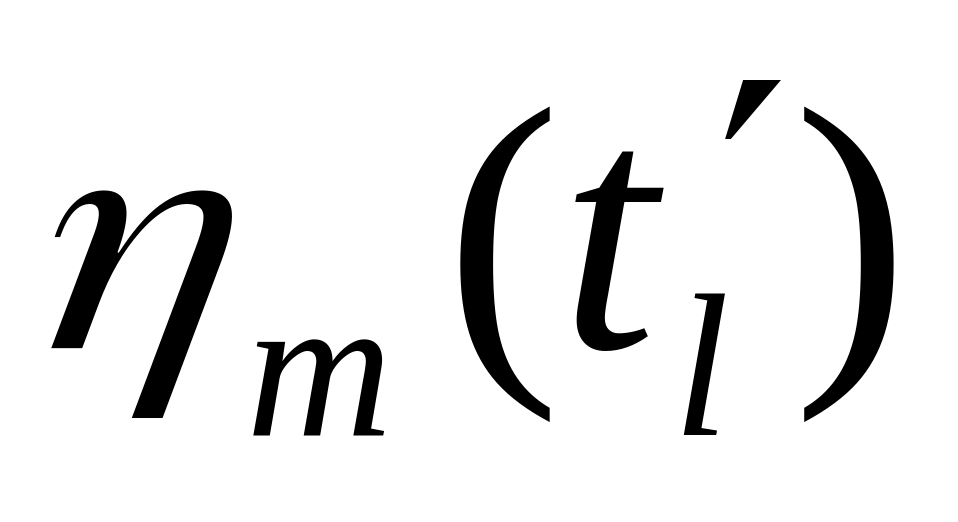 -
).
Если
-
).
Если
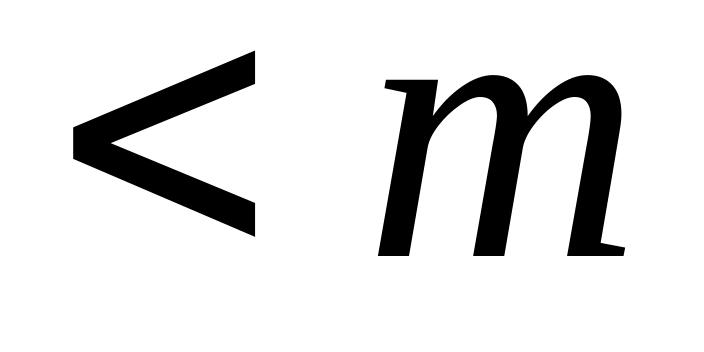 ,
то генерируется случайная величина
,
то генерируется случайная величина
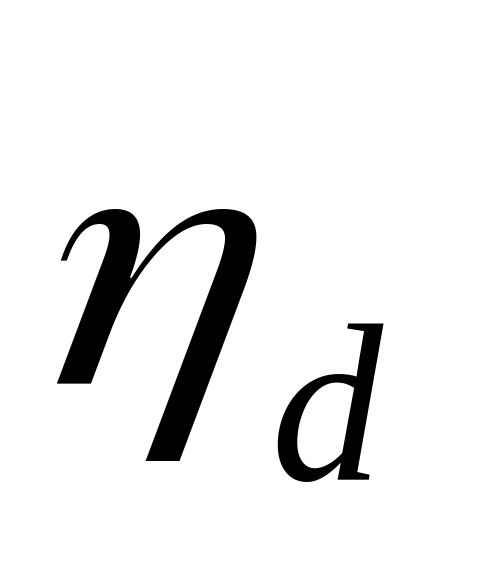 ,
которая будет помещена в ячейке, в
которой находился 0, как символ свободности
канала обслуживания. В счетчик
длительностей интервалов заносится
пара (
,
,
которая будет помещена в ячейке, в
которой находился 0, как символ свободности
канала обслуживания. В счетчик
длительностей интервалов заносится
пара (
,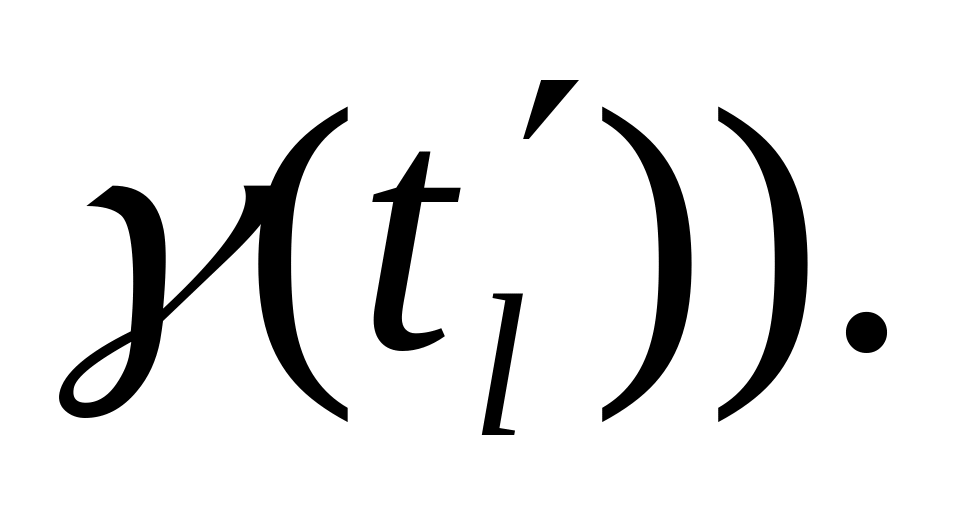
Если ( =
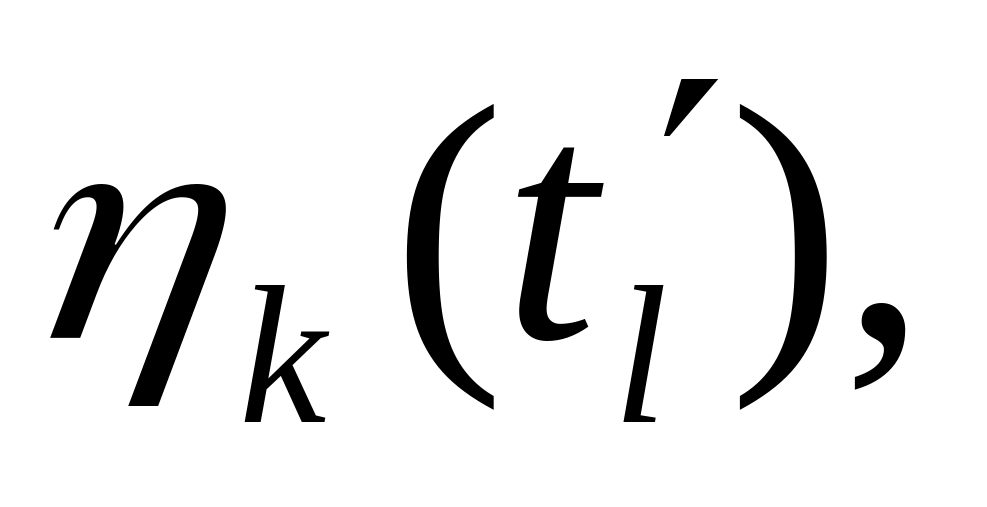 ,
то модельное время увеличивается на
величину
в ячейку для
заносится величина
-
в ячейку для
заносится величина
-1, величины
,
то модельное время увеличивается на
величину
в ячейку для
заносится величина
-
в ячейку для
заносится величина
-1, величины
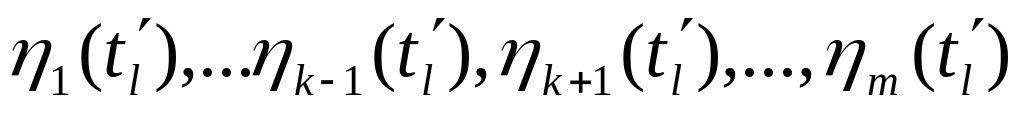 уменьшаются на величину
в ячейку для
уменьшаются на величину
в ячейку для
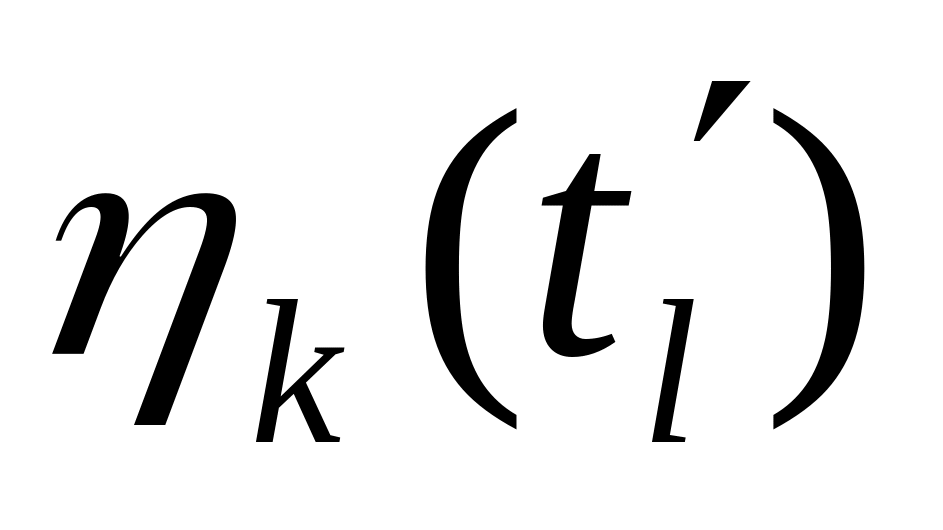 заносится величина времени обслуживания
следующего требования, которое является
первым требованием в очереди, если
заносится величина времени обслуживания
следующего требования, которое является
первым требованием в очереди, если
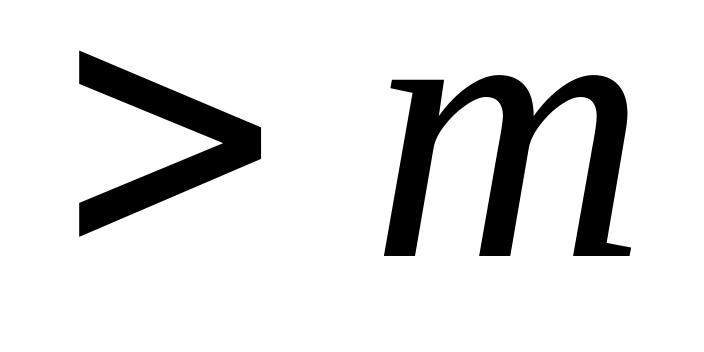 ,
и 0 в противном случае. Таким образом,
=
(
,
будет равен (
=
-1 ,
,
и 0 в противном случае. Таким образом,
=
(
,
будет равен (
=
-1 ,
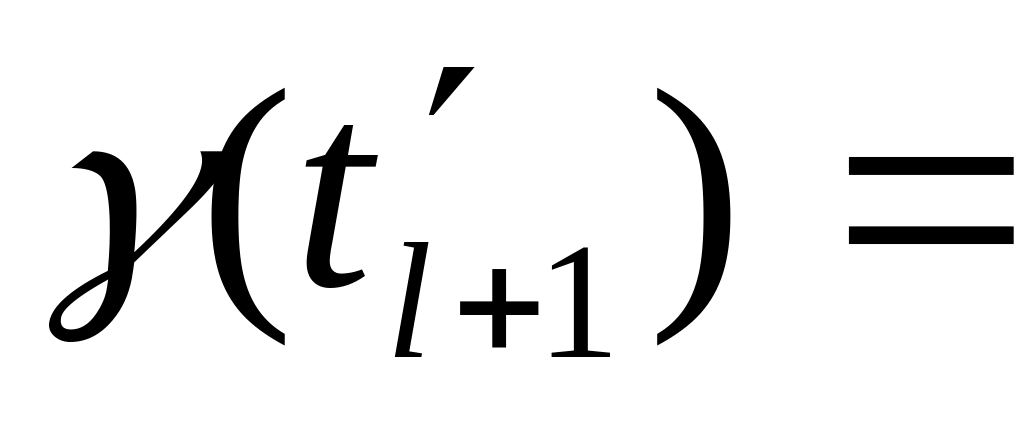 -
-
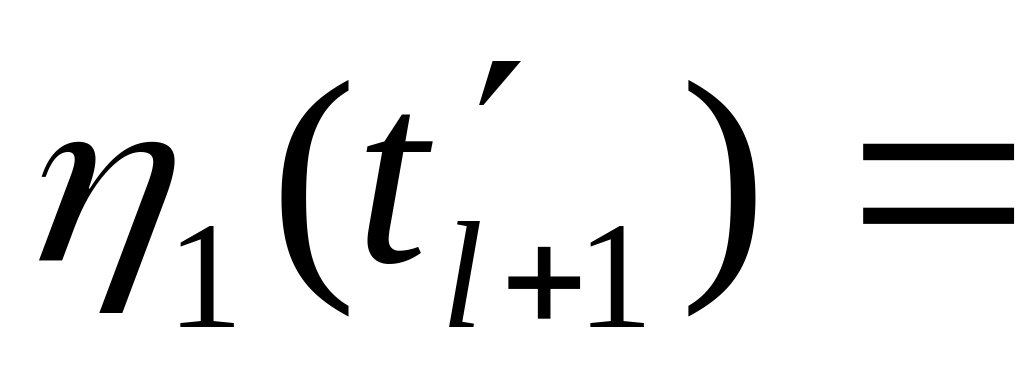 …,
…,
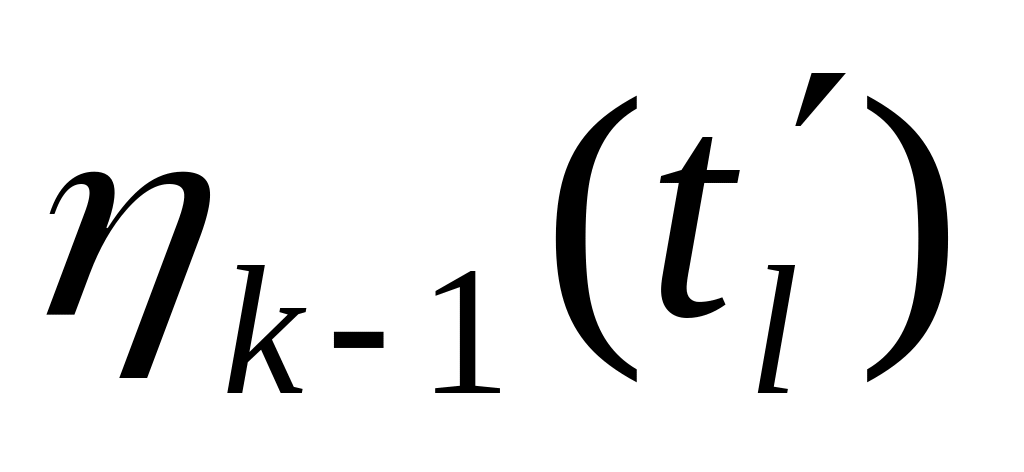 -
-
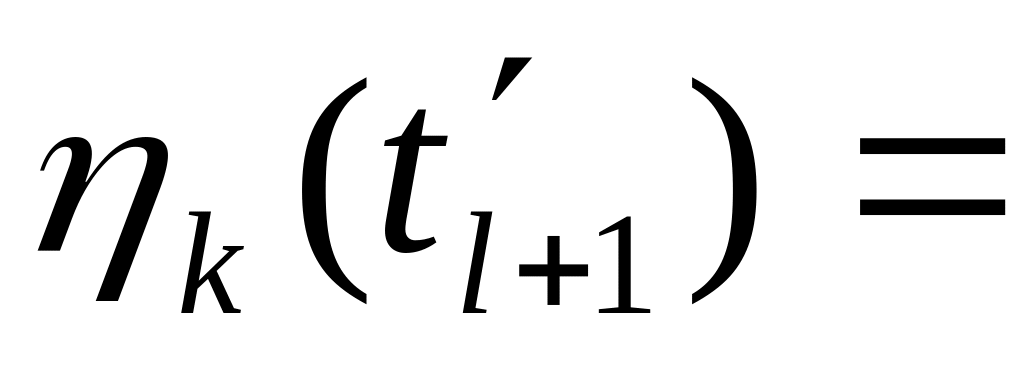 )+0
(1-
)),
)+0
(1-
)),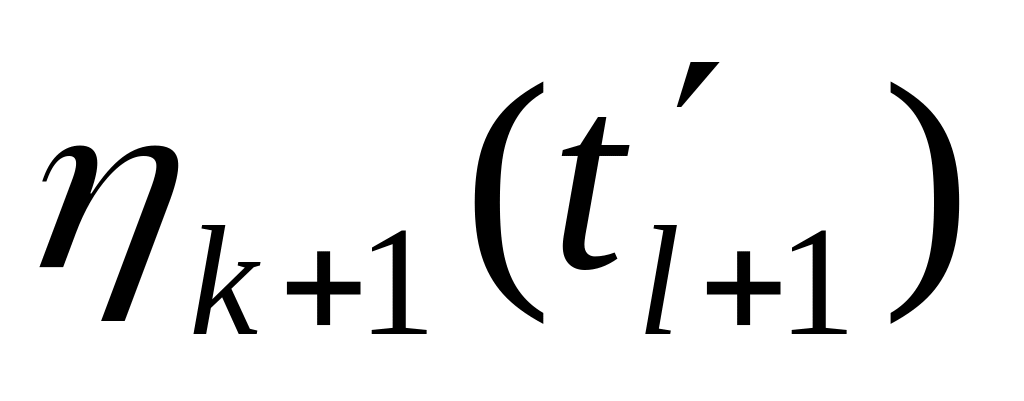 =
=
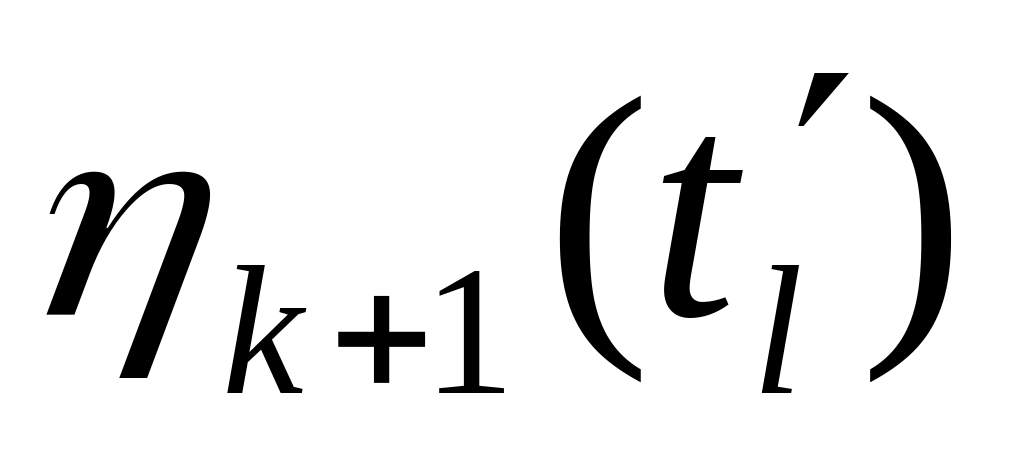 -
…,
=
-
).
В счетчик длительностей интервалов
заносится пара (
,
-
…,
=
-
).
В счетчик длительностей интервалов
заносится пара (
, .
.В счетчике числа скачков прибавляется 1 и по циклу переходим к п. 1.
Кончается период занятости уменьшением до 0.
Каждый период занятости можно моделировать автономно, т.к. развитие процесса на нем не зависит от того, что происходило до момента начала этого периода занятости. Момент его начала есть точка регенерации процесса . Но всю статистику необходимо засылать в счетчик длительностей интервалов. Свободные периоды после каждого периода занятости свойством регенерации не обладают, но их также надо засылать в счетчик длительностей интервалов.
