1.5.3. Методы генерирования цепей и процессов Маркова.

Простая цепь Маркова полностью характеризуется матрицей переходных вероятностей { p_ij }.

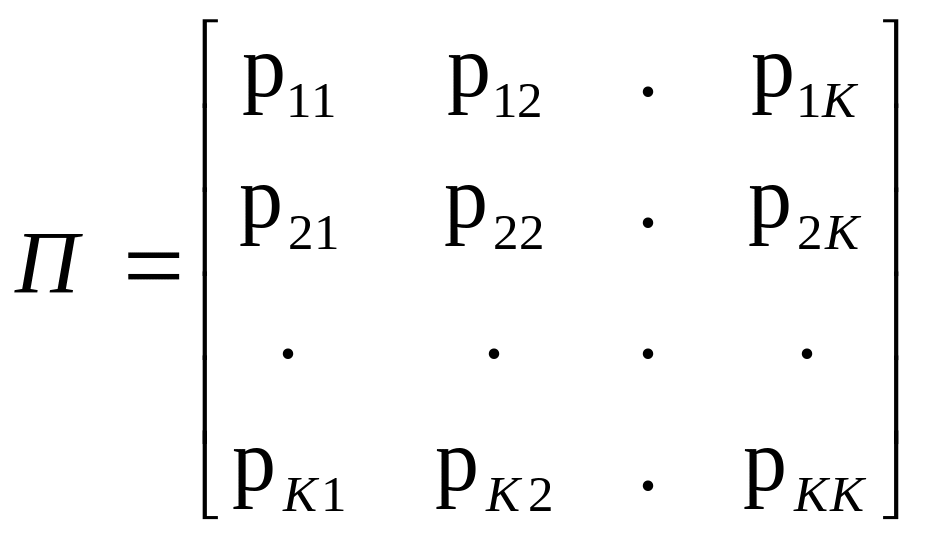
Будем рассматривать вероятности Р_ij матрицы переходных вероятностей, как условные вероятности наступления в данном испытании события A_j , при условии, что результатом предыдущего испытания было событие А_i .

Моделирование цепи Маркова в этом случае состоит в последовательном выборе событий А_j в соответствии с заданными переходными вероятностями. Сначала выбирается некоторое начальное состояние цепи Маркова, которое может быть задано априорно, либо выбирается по жребию.

Пусть начальным состоянием будет состояние А_l , которое задается вероятностями p_l1, p_l2, . . ., p_lK , образующими l - строку матрицы переходных вероятностей.

Так как сумма вероятностей в l-ой строке тождественно равна единице, то формируется число  , равномерно распределенное на интервале [0, 1] и проверяется в какой из интервалов p_lj = _i это число попадает:

(1)

Пусть число  попало в интервал, соответствующий m-му состоянию. Это означает, что следующим событием данной реализации цепи Маркова будет событие А_m . Выбирается m-ая строка матрицы {Р_ij}, вновь формируется число  и проверяется условие (1) , но уже для m-ой строки. Аналогичная процедура повторяется и далее.

1.5.4. Метод генерирования процессов Маркова с дискретным множеством состояний.

Процессы Маркова с дискретным множеством состояний задаются: дискретным множеством состояний и интенсивностями переходов из одного состояния в другое состояние , . Интенсивность выхода из состояния определяется через интенсивности переходов следующим образом

= .

Тогда моделирование процесса Маркова с дискретным множеством состояний осуществляется следующим образом: генерируется по вышеизложенному случайная величина, имеющая экспоненциальное распределение с параметром , а затем осуществляется переход в , , с вероятностями

, рассчитываемыми по следующей формуле

= .

1.5.5. Метод генерирования процессов Маркова с дискретно-непрерывным множеством состояний.

Процессы Маркова с дискретно-непрерывным множеством состояний задаются: дискретным множеством состояний , дискретным вектором состояния и множеством непрерывных компонент , где - количество непрерывных компонент в дискретном векторе состояния . В дискретном состоянии находится минимум . Пусть он достигается на компоненте . Тогда модельное время сдвигается на величину , из дискретного состояния осуществляется переход в дискретное состояние с переходной вероятностью , = 1.

Моделирование этого процесса осуществляется следующим образом. Разыгрывается начальное дискретное состояние процесса с непрерывными компонентами . Далее находится минимальная компонента из . Пусть минимум достигается на компоненте . Тогда модельное время сдвигается на величину , из дискретного состояния осуществляется переход в дискретное состояние с переходной вероятностью , = 1 и так далее.