
- •Введение
- •Глава 1. Моделирование случайных величин
- •1.1.1. Понятия модели и моделирования
- •1.1.2. Основной цикл познания при моделировании
- •1.1.3. Математическое моделирование
- •1.1.3.1. Математическое описание сложных систем
- •1.1.3.2. Методы математического моделирования
- •1.1.3.3. Имитационное моделирование
- •1.1.3.4. Принципы построения алгоритмов имитационного моделирования
- •1.1.3.5. Характерные особенности имитационного моделирования на эвм
- •1.1.3.6. Статистическое моделирование
- •1.1.3.7. Понятие о вероятностном физическом моделировании
- •1.1.3.8. Достоинства метода имитационного моделирования на эвм
- •1.1.3.9. Недостатки метода имитационного моделирования
- •1.2. Структура имитационной модели. Технологии построения.
- •1.2.1. Этапы разработки имитационной модели
- •1.2.2. Элементы и структура имитационной модели
- •1.2.3. Технология построения и функционирования.
- •1.3. Генерирование равномерно распределенных на интервале [0,1] случайных чисел. Проверка качества генераторов случайных чисел
- •1.3.1. О приближенных случайных числах
- •Физические датчики случайных величин
- •О проверке физических датчиков случайных чисел
- •Метод псевдослучайных чисел
- •Алгоритмы получения псевдослучаных чисел
- •Алгоритмы порядка r
- •Метод возмущений
- •Генератор Лемера
- •Проверка качества формируемой последовательности псевдослучайных чисел
- •1.4. Методы генерирования случайных событий, дискретных и непрерывных случайных величин, многомерных случайных величин, усеченных случайных величин.
- •1.4.1. Моделирование дискретных случайных величин
- •1.4.2. Моделирование семейства биномиальных распределений
- •1.4.3. Моделирование непрерывных случайных величин Метод обратных функций
- •Метод суперпозиций
- •Моделирование многомерных случайных величин
- •Моделирование n-мерной точки с зависимыми координатами
- •Метод отбора
- •Применение метода отбора. Моделирование усеченных распределений
- •Метод Неймана
- •Выбор равномерно распределенных точек в сложных областях
- •1.5. Методы генерирования наиболее часто встречающихся на практике распределений.
- •1.5.1. Моделирование распределения Эрланга
- •1.5.2. Приближенное моделирование нормально распределенных случайных величин
- •1.5.3. Методы генерирования цепей и процессов Маркова.
- •1.5.4. Метод генерирования процессов Маркова с дискретным множеством состояний.
- •1.5.5. Метод генерирования процессов Маркова с дискретно-непрерывным множеством состояний.
- •Глава 2. Моделирование информационных систем железнодорожного транспорта
- •2.1. Формирование реализаций случайных потоков
- •Однородных событий.
- •2.1.1. Входящие потоки
- •2.1.2. Формирование произвольных случайных потоков однородных событий
- •2.2. Введение марковских процессов при моделировании систем массового обслуживания при произвольных распределениях основных случайных величин.
- •2.3. Моделирование однолинейной системы массового обслуживания
- •2.3.1. Распределение длины очереди
- •2.3.2. Время отклика и время ожидания
- •2.4. Моделирование многолинейной системы массового обслуживания
- •2.4.1. Моделирование многолинейной системы массового обслуживания для расчете времени ожидания
- •2.4.2. Моделирование многолинейной системы массового обслуживания для расчета распределения числа требований в системе.
- •2.5. Моделирование сетей массового обслуживания,
- •Глава 3. Оценка точности результатов моделирования
- •3.1. Постановка задачи по оценке точности результатов моделирования. Характеристики точности результатов моделирования Оценка точности результатов аналитического моделирования
- •3.1.1. Постановка задачи по оценке точности результатов
- •3.1.2. Классификация входных случайных величин
- •3.1.3. Смещение и дисперсия оценки выходного показателя
- •3.2. Оценка точности результатов имитационного
- •3.2.1. Оценка смещения
- •3.2.2. Оценка составляющей дисперсии за счет неточности входных параметров
- •3.2.3. Оценка частных производных от показателя эффективности сложной системы на ее математической модели
- •3.3. Оценка точности результатов статистического
- •Глава 4. Разработка математической модели функционирования двухпутного железнодорожного участка для определения минимального расчетного межпоездного интервала
- •4.1. Постановка задачи
- •4.1.1. Актуальность разработки модели
- •4.1.2. Постановка задачи по разработке модели.
- •4.2.2. Кусочно-непрерывный марковский процесс, описывающий функционирование двухпутного железнодорожного участка
- •4.3. Алгоритм смены состояний кусочно-непрерывного процесса, функционирования железнодорожного участка во времени
- •4.4. Уравнения движения поезда
- •4.5. Программная реализация алгоритма математической модели функционирования двухпутного ж.Д. Участка
- •4.6. Оценка точности линеаризованных решений дифференциальных уравнений движения поезда
- •4.7. Результаты моделирования
- •4.7.1. Описание объекта моделирования и исходные данные
- •4.8. Результаты моделирования для обычных грузовых поездов
- •4.9. Результаты моделирования для поездов повышенной длины и массы
- •4.10. Результаты расчета точности решений линеаризованных уравнений движения поезда
- •Глава 5. Задачи по дисциплине «Моделирование систем» для студентов 4 курса по кафедре «асу» по направлениям
- •Оглавление
- •Глава 1
- •Глава 2. Моделирование информационных систем
- •2.3. Моделирование однолинейной системы массового обслуживания………………………………………………………………...52
- •2.4. Моделирование многолинейной системы массового обслуживания..55
- •Глава 3. Оценка точности результатов моделирования…………………...63
- •Глава 4. Разработка математической модели функционирования
- •Глава 5. Задачи по дисциплине «Моделирование систем»
Метод Неймана
Рассмотрим случайную величину , определенную на интервале [а, в] с плотностью распределения f(х). Причем плотность распределения ограничена сверху f(х) < С . Эта плотность распределения изображена на рис. 1.5.
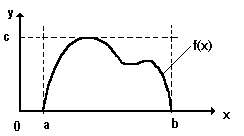
Рис. 1.5.
Теорема 3. Пусть 1 и 2 независимые, равномерно распределенные на интервале [0, 1] случайные числа. Случайная величина , определенная соотношениями = / < f ( ), где =а + 1(в-а), = С2 , имеет заданную плотность распределения f(х).
Доказательство. Пусть двумерная точка с координатами ( , ) имеет равномерное распределение в прямоугольнике, т.е. ее плотность = [c(b-a)]-1
Имеем
![]()
![]()
![]()
Рассмотрим числитель, который представляет собой вероятность одновременного выполнения двух условий: точка ( , ) окажется под кривой плотности распределения и в то же время < z :
![]()
Отсюда
![]()
Эффективность
метода Неймана равна
![]() .
.
Выбор равномерно распределенных точек в сложных областях
Пусть В - ограниченная область на плоскости х, y , “сложная” с точки зрения вычислительной практики: например, границы на отдельных участках трудно задать в явном виде. Предположим, что существует достаточно простой алгоритм, позволяющий определить, принадлежит ли области В любая заданная точка {х, y} или нет.
Выберем прямоугольник П = {а1 < х < в1, а2 < y < в2}, содержащий область В. Он изображен на рис. 1.6.
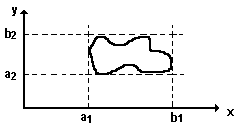
Рис. 1.6.
Координаты случайной точки Q = { , }, равномерно распределенной в прямоугольнике П, легко вычислить:
![]()
Для нахождения точек Q, равномерно распределенных в В, можно формировать точки Q , равномерно распределенные в прямоугольнике П и отбирать среди них те, которые принадлежат области В.
Эффективность
такого метода равна отношению площадей
области G и прямоугольника П
![]() .
.
1.5. Методы генерирования наиболее часто встречающихся на практике распределений.
1.5.1. Моделирование распределения Эрланга
Это распределение очень часто встречается на практике, поскольку позволяет аппроксимировать широкий класс статистических рядов, за счет того, что при изменении порядка распределения удается описать как асимметричные распределения, так и симметричные, например, нормальное.
Пусть случайная величина n описывается распределением Эрланга n-го порядка, имеющим плотность следующего вида:
![]() ,
,![]() ,
,
![]()
Распределение
Эрланга представляет собой распределение
суммы
независимых слагаемых, каждое из которых
имеет экспоненциальное распределение
с параметром
![]() .
Его моделирование сводится к получению
реализаций случайной величины, имеющей
экспоненциальное распределение с
параметром
,
и их суммированию.
.
Его моделирование сводится к получению
реализаций случайной величины, имеющей
экспоненциальное распределение с
параметром
,
и их суммированию.
Поток Эрланга может быть получен путем просеивания простейшего потока через n-1 событие поступления его требования.
1.5.2. Приближенное моделирование нормально распределенных случайных величин
Основано на использовании центральной предельной теоремы теории вероятности, утверждающей, что сумма большого числа независимых, одинаково распределенных случайных величин с конечным математическим ожиданием и дисперсией, асимптотически распределена нормально.
Будем считать, что в качестве исходных используются равномерно распределенные на интервале [0, 1] независимые случайные числа 1, 2 , . . . n. Математическое ожидание и дисперсия случайных чисел равны
![]()
Введем в рассмотрение случайную величину i , выполнив операции центрирования и нормирования:
![]() .
.
Определим случайную величину n следующим образом:
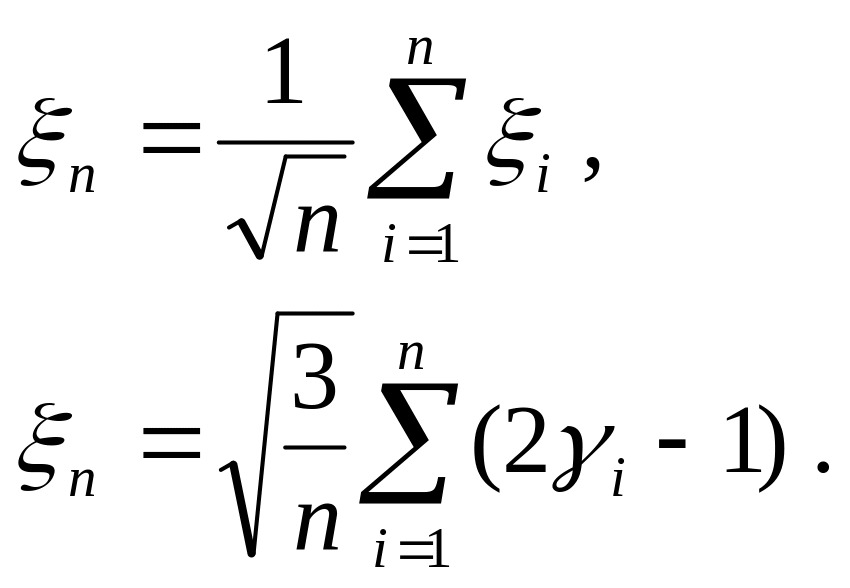
Закон распределения
случайной величины n при
![]() будет асимптотически нормальным с
параметрами m
= 0,
= 1.
будет асимптотически нормальным с
параметрами m
= 0,
= 1.
Варьируя числом слагаемых n в формуле (3.13) осуществляется приближенное моделирование нормально распределенных случайных величин.
В частном случае
при n =12 имеем
![]() .
.
Поскольку при моделировании на ЭВМ используются псевдослучайные числа, то возможны ситуации ухудшения качества формирумой последовательности случайных величин. Поэтому выбор числа слагаемых n представляет собой отдельную задачу построения качественного датчика нормально распределенных случайных величин.
Для того, чтобы получить нормально распределенные случайные величины с заданными параметрами { m , }, поступают следующим образом:
![]()
Следует отметить, что задача моделирования нормально распределенных случайных величин часто встречается на практике, поэтому при построении датчика целесообразно проанализировать все методы и выбирать тот, который обеспечивает наиболее качественную последовательность случайных чисел.
