Моделирование многомерных случайных величин

Моделирование случайных величин с независимыми координатами производится покоординатно в соответствии с вышеприведенными алгоритмами

Моделирование n-мерной точки с зависимыми координатами

Когда координаты точки Q являются зависимыми, совместную плотность f_Q (x₁, x₂, . . . x_n) распределения координат точки Q можно представить в виде произведения условных плотностей распределения:

f_Q (x₁, x₂, . . . x_n) = f₁(x₁)  f₂ (x₂/x₁)  f₃ (x₃/x₁,x₂)  . . .  f_n (x_n/x₁,x₂, ...x_n-1)

В качестве исходной информации при моделировании точек с зависимыми координатами используется совместная плотность распределения координат точки Q. На ее основании можно вычислить плотности распределения всех координат.

Приведем выражения для условных плотностей распределения в общем виде, проводя интегрирование в пределах [ -,  ] :

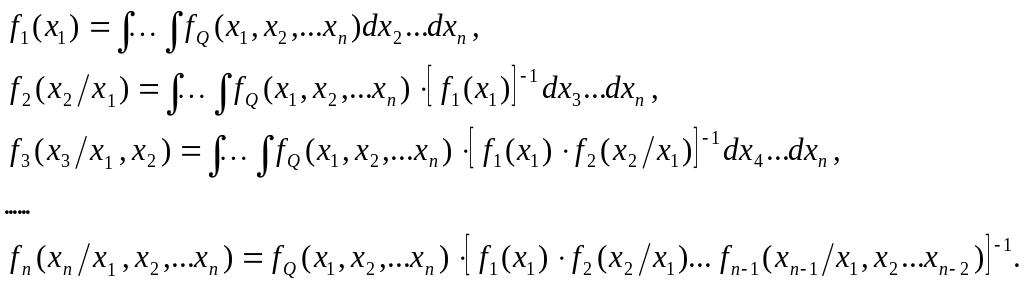
По условным плотностям распределения всегда можно найти условные функции распределения

Теорема. Об обратных функциях в многомерном случае

Пусть ₁, ₂, ... _n - независимые равномерно распределенные на интервале [0, 1] случайные числа. Совокупность случайных величин ₁, ₂, . . . _n , полученных в результате последовательного решения уравнений:

имеет заданную совместную плотность распределения f_Q (x₁, x₂, . . . x_n).

Особенность, с которой приходится сталкиваться при моделировании многомерных случайных величин, заключается в том, что представление n-мерной совместной плотности в виде произведения безусловной и условных плотностей распределения возможно различными способами, число которых равно n!.

Правильный выбор безусловной плотности распределения может существенно упростить соотношения для моделирования координат случайной точки Q.

Метод отбора

Предположим, что в m-мерном пространстве переменных y₁, y₂, . . . y_m заданы случайная точка Q с координатами {₁, ₂, . . . _m} с известной функцией распределения F_Q(y₁, y₂, . . . y_m), а также некоторая область этого пространства В. Рассмотрим одномерную случайную величину  , определенную следующим образом:

. (1.4.4)

Считается, что вид зависимости  (  ) задан.

Для расчета по формуле (1.4.4) необходимо:

- одним из рассмотренных методов сформировать точку Q с заданными координатами;

- проверить условие принадлежности точки Q заданной области В. Здесь возможны два исхода:

а) тогда ;

б) в этом случае точка Q отбрасывается и формируется новая точка Q.

Считается, что соотношение (1.4.4) определяет метод отбора.

Поскольку при реализации изложенной процедуры часть точек Q не используется для расчета значений случайной величины  (т.е. отбрасывается), то вводится понятие эффективность метода отбора.

Эффективностью метода отбора называют вероятность отбора или, более подробно, вероятность того, что точка Q будет использована для расчета значения . Очевидно, эффективность метода равна вероятности:

.

Применение метода отбора. Моделирование усеченных распределений

Будем считать, что задана случайная величина  , определенная на интервале [а, в] с плотностью распределения f(х), причем:

Говорят, что случайная величина  имеет усеченное распределение

f_ (х), если ее плотность распределения пропорциональна f(х):

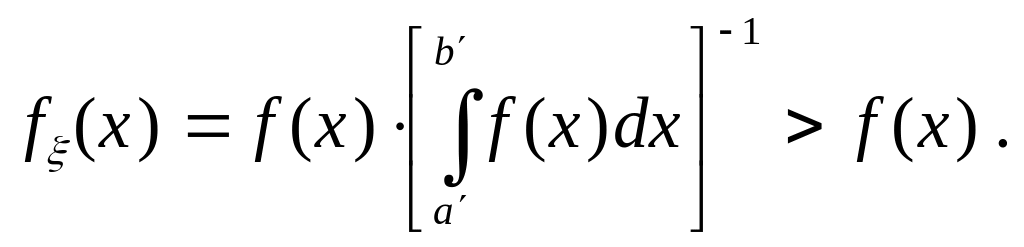
Если задана плотность распределения f(x) неусеченной случайной величины, то кривая плотности распределения f_(x) усеченной случайной величины располагается выше, как показано на рис. 3.9, где а = а = 0, в = .

Рис. 1.4.

Чтобы смоделировать значение случайной величины  , одним из известных методов формируют значение случайной величины  с плотностью распределения f (х), а затем применяется метод отбора  =  , если .

Эффективность этого метода равна