1.4.2. Моделирование семейства биномиальных распределений

Задана случайная величина  , имеющая биномиальное распределение: Один из путей моделирования случайной величины  заключается в том, что на основании можно записать ее ряд распределения и моделирование свести к рассмотренным ранее случаям.

Однако этот путь имеет существенный недостаток - большая подготовительная работа перед вычислениями.

Более предпочтителен другой способ моделирования, когда при фиксированной вероятности р можно воспроизводить условия возникновения биномиального распределения - схему независимых испытаний.

В этом случае формируется последовательность псевдослучайных чисел  и n раз проверяется условие ₁ < p ,₂ < p , ₃ < p,_n < p . В данной серии из n чисел условие ( _i < p ) будет выполняться, например, раз.

Считается, что - конкретное значение случайной величины  в данной серии опытов. Сформировав вновь n чисел , и проверив условие (3.4), определим новое значение  и т.д.

1.4.3. Моделирование непрерывных случайных величин Метод обратных функций

Полной характеристикой непрерывной случайной величины является закон распределения, заданный функцией распределения или плотностью распределения.

Обозначим F(х) - функцию распределения случайной величины .

Теорема 2 (об обратных функциях). Случайная величина , удовлетворяющая условию:

F (  ) =  , (1.4.3)

имеет заданный закон распределения (х).

Доказательство. Имеем

.

Пример.

Задана случайная величина  с законом распределения = 1-e^-х на интервале [ 0< х <  ]. Получим соотношение для моделирования значений величины .

На основании метода обратных функций можно записать следующее соотношение:

F (  ) =  или 1 - e^- =  .

Заметим, что поскольку случайная величина (1 -  ) имеет то же распределение, что и  , выражение для формирования случайной величины  можно упростить:

1 - e^- = 1 -  , откуда

Нередко метод обратных функций приводит к сложным или просто неудобным алгоритмам. Например, для того, чтобы формировать значения случайной величины с нормальным распределением (с параметрами [0, 1]), приходится решать уравнение

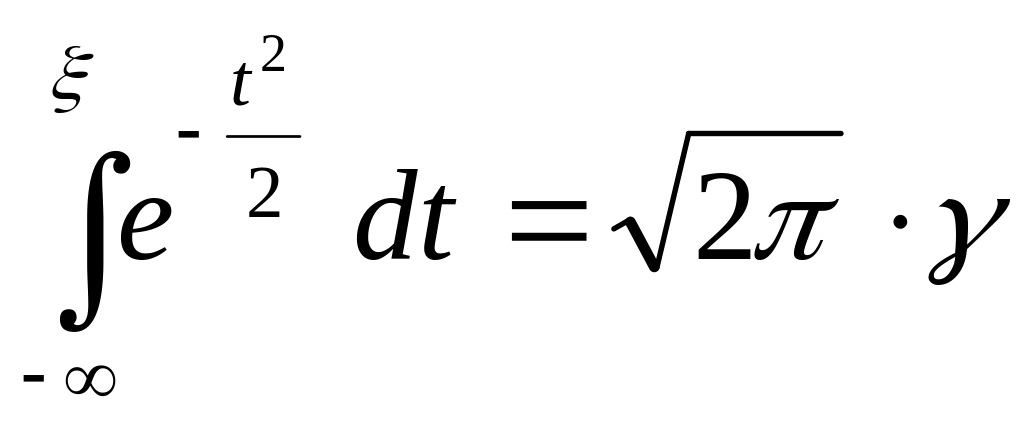
В таких случаях обычно используют методы формирования значений случайных величин, связанные с другими преобразованиями равномерно распределенных чисел .

Метод суперпозиций

Пусть задана функция распределения F (х) случайной величины , которая может быть представлена следующим образом: , т.е. в виде смеси некоторых функций распределения F_K (х), а сумма всех коэффициентов С_К равна 1:

Введем в рассмотрение дискретную случайную величину , задав ее рядом распределения

	1	2	3	. . .	m
р	C1	C2	C3	. . .	Cm

Пусть ₁ и ₂ - независимые равномерно распределенные случайные числа. Если по числу ₁ произвести выбор интервала (значения случайной величины  = к), а по числу ₂ в результате решения уравнения F_K(  ) =₂ определить величину , то величина  будет иметь заданный закон распределения F(х).