1.4. Методы генерирования случайных событий, дискретных и непрерывных случайных величин, многомерных случайных величин, усеченных случайных величин.

1.4.1. Моделирование дискретных случайных величин

Будем считать, что задана дискретная случайная величина  , представленная рядом распределения.

Для моделирования значений дискретной случайной величины  разделим единичный интервал [0; 1] на n непересекающихся отрезков длиной _i = p_i (см.рис. 3.1).

Предположим, что в нашем распоряжении имеется совокупность случайных чисел ₁, ₂, . . . _N , являющихся выборкой равномерно распределенной на интервале [0; 1] случайной величины  .

Выбирая очередное значение _j и проверяя, в какой из интервалов _i это значение попадает (см. рис. 3.1), по номеру i интервала разбиения определяется конкретное значение случайной величины  .

₁ ₂ ₃ ₄ ₅    _n

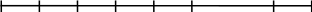
0 1

Рис.1.3.

Теорема 1. Случайная величина , определенная соотношением (1.4.1)

 = х_i , если   _i , (1.4.1)

имеет заданный закон распределения, представленный в виде ряда распределения

		…
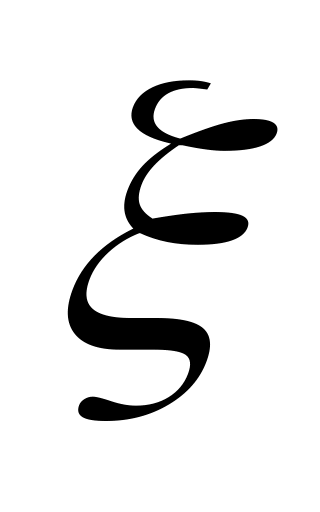
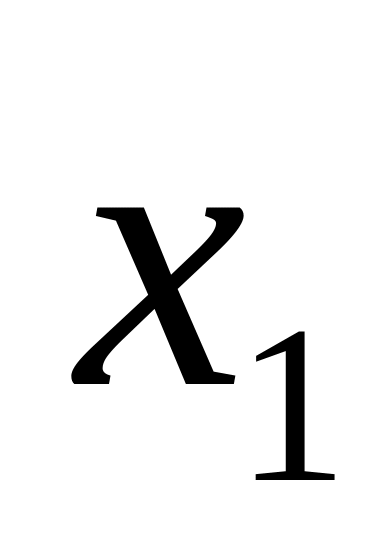
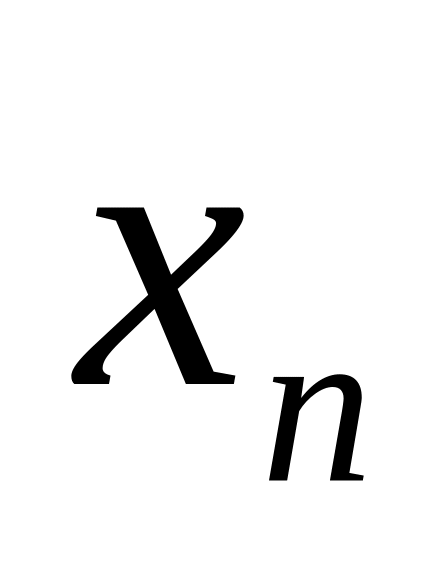
р		…

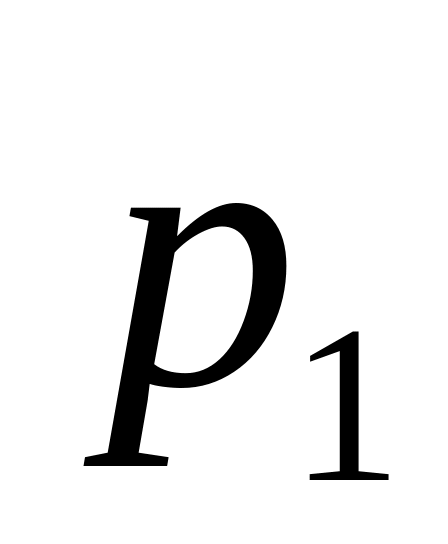
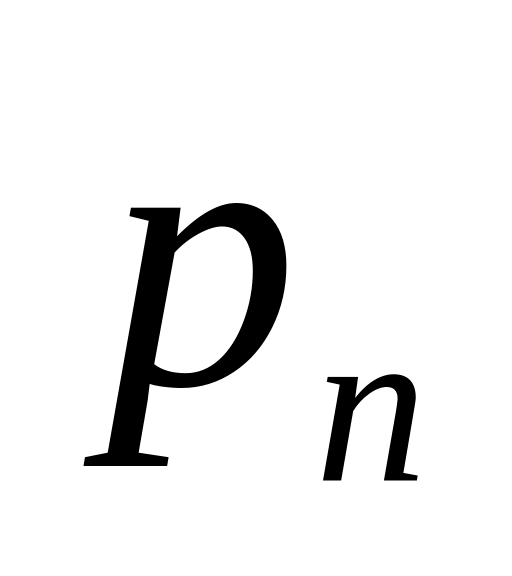
Доказательство. Рассмотрим вероятности:

Р { = x_i} = P {  _i} = длина _i = p_i ,

что и требовалось доказать.

Для того, чтобы проверить какому интервалу разбиения _i принадлежит случайное число  , в памяти ЭВМ подряд располагаются значения х₁, х₂, х₃, . . . х_n и значения р₁, р₁+ р₂, р₁+ р₂+ р₃, . . . 1 .

Формируя число , его сначала сравнивают с р₁; если  < p₁ , то  = х₁ .

Если это условие не выполняется, то  сравнивается с р₁ + р₂ . При условии, что  < р₁ + р₂ , то  = х₂. Если и это условие не выполняется, то  сравнивают с р₁ + р₂ + р₃ и т.д.

Возникает вопрос, каким образом располагать значения вероятностей в памяти ЭВМ, чтобы количество сравнений было минимальным.

В том случае, когда  = х_i (1 < i < n-1) , количество сравнений, необходимое для определения значения , равно i . И только когда  = х_n , количество сравнений будет равно n - 1.

Следовательно, среднее количество t сравнений, необходимое для определения значения величины :

( 1.4.2 )

Величина t будет минимальной, если расположить значения p_i в порядке убывания соответствующих вероятностей p₁  p₂  p₃  . . .  p_n .

Моделирование случайных событий проводится на основе схемы моделирования дискретных случайных величин.

Моделирование отдельного случайного события

В соответствии с доказанной выше теоремой для проведения каждого испытания необходимо сформировать число  и проверить условие :  < p_А. Если это условие выполняется, то наступило событие А, если не выполняется, то наступило событие А.

Моделирование полной группы случайных событий

События А₁, А₂, . . . А_n составляют полную группу с вероятностями р₁, р₂, . . . , р_n . Введем в рассмотрение дискретную случайную величину , имеющую смысл номера события полной группы:

В соответствии с доказанной выше теоремой формируются числа  , проверяется в какой из интервалов _i они попадают. Номер этого интервала определяет индекс события А_i .

Моделирование совместных независимых событий

Пусть заданы совместные независимые события А и В. Известны вероятности наступления событий Р_А и Р_В, соответственно.

Моделирование указанных событий может осуществляться двумя способами:

1. С использованием двух случайных чисел ₁ и ₂ .

С помощью числа ₁ проверяется условие: ₁ < р_А . Если условие выполняется, то считается, что наступило событие А. В противном случае - .

С помощью числа ₂ проверяется условие ₂ < p_В . При выполнении условия наступило событие В, в противном случае .

Недостаток данного способа моделирования заключается в том, что при использовании двух чисел ₁ и ₂ возрастают затраты машинного времени, связанные с обращениями к датчикам .

2. С использованием одного числа  , но предполагающее некоторую предварительную подготовку.

Определяется полная группа событий: и соответствующий ей ряд распределения :


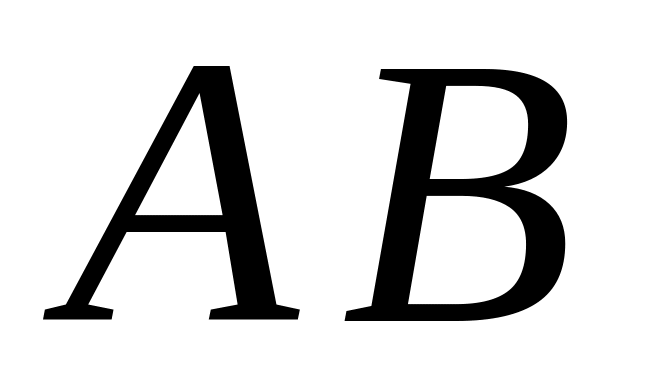
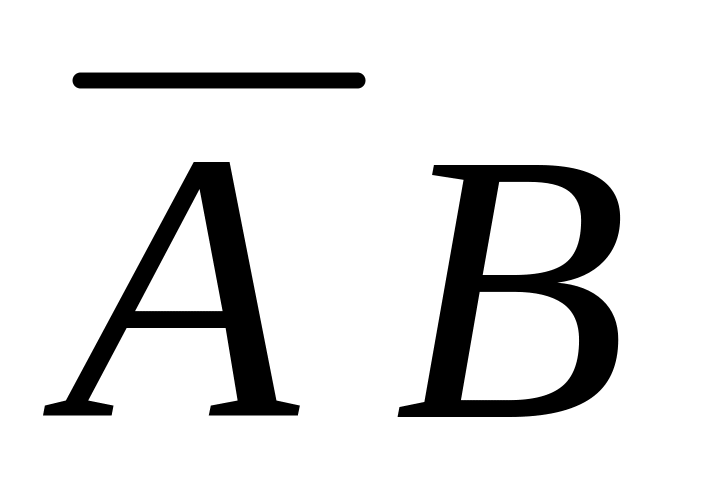
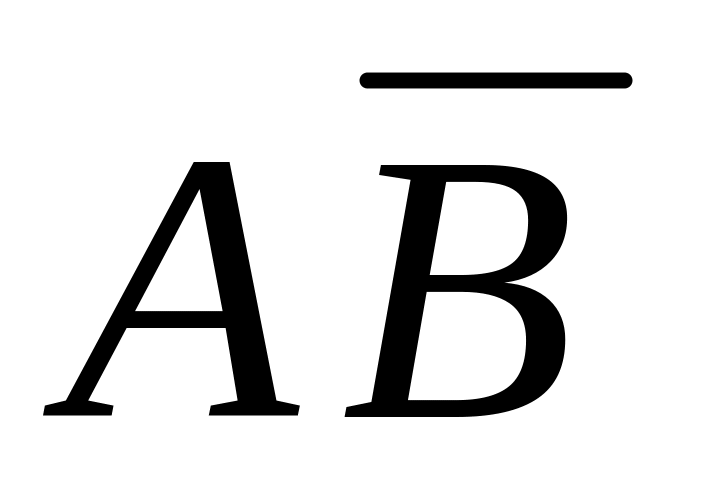
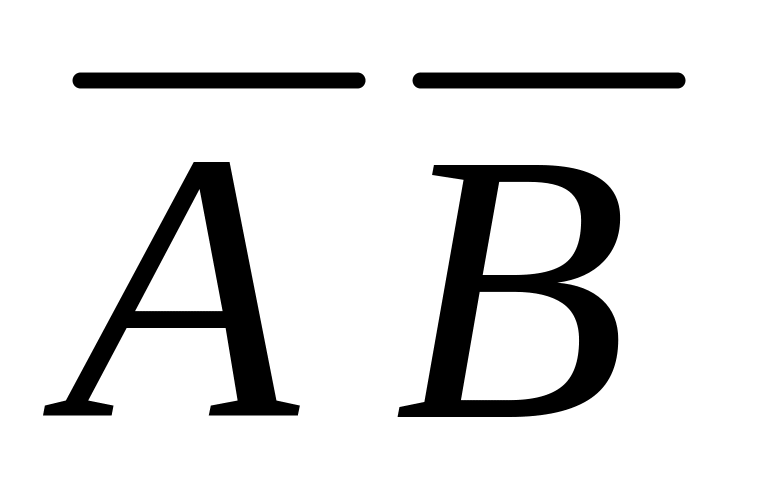
р	рАрВ	(1-рА)рВ	рА(1-рВ)	(1-рА)(1-рВ)

Получив ряд распределения, моделирование сводится к ранее рассмотренной схеме моделирования полной группы событий.

Моделирование совместных зависимых событий.

В качестве исходной информации используются вероятности Р_А , Р_В , Р_АВ .

Моделирование также может осуществляться двумя способами:

1. С использованием двух чисел ₁ и _{2 .}

По числу ₁ проверяется наступление события А. Если А наступило, то по условной вероятности Р (В/А) с помощью числа ₂ определяется, наступило ли событие В - ₂ < р (В/А) .

Если событие А не наступило, то наступление события В проверяется с помощью условной вероятности .

2. Моделирование осуществляется с использованием одного числа  по рассмотренной выше схеме моделирования полной группы событий, вероятности которых вычисляется следующим образом:


р	рАВ	рА - рАВ	рВ - рАВ	1 -рА - рВ + рАВ