2.2. Практика розкриття невизначеностей виду та .

Користуючись правилом Лопіталя, знайти вказані границі:

1) Безпосередня підстановка граничного значення аргументу x=1 приводить до невизначеності виду . Так як функції і задовольняють умовам теореми Лопіталя, то згідно з (1) будемо мати

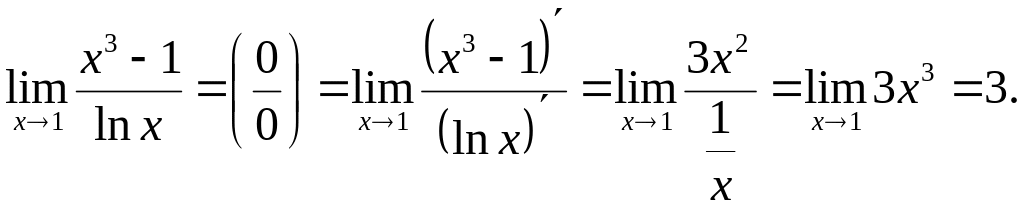
Примітка. Обчислення границі згідно з правилом Лопіталя зазвичай записують зразу. В існуванні необхідних похідних і границь переконуються безпосередньо в процесі обчислень. Тому попередні викладки можуть бути опущені, що й рекомендуємо робити в подальшому.

2) 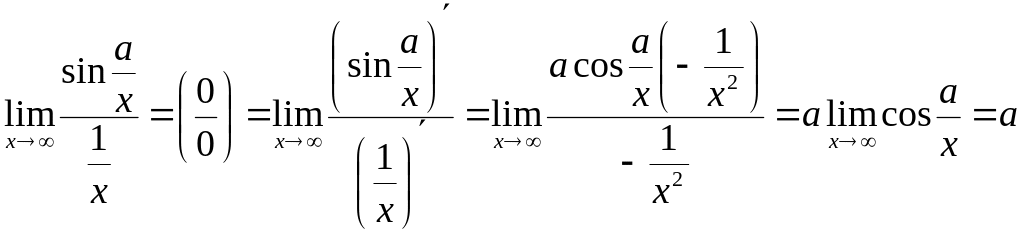,де a=const. 3)

Розглянемо приклади, коли правило Лопіталя при знаходженні границі застосовується повторно.

4)

5) При , залишаючись додатним, маємо невизначеність виду яку потрібно розкрити. За правилом Лопіталя маємо

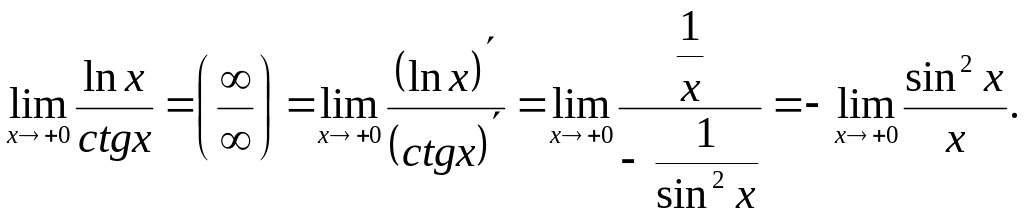
Остання границя при дає невизначеність виду . Можливі два шляхи для її розкриття: а) повторно застосувати правило Лопіталя; б) скористатись теоремою про границю добутку двох функцій.

З огляду на сказане маємо

а)

б)

Наведемо ще декілька прикладів, коли правило Лопіталя приходиться комбінувати з іншими методами знаходження границі.

6)

.

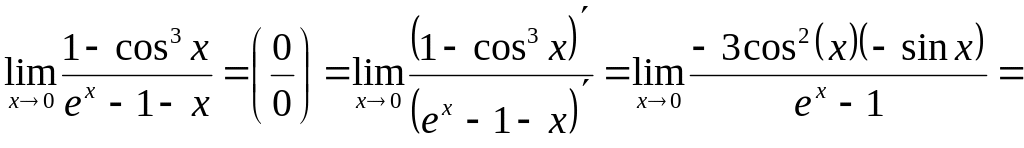
7)

.

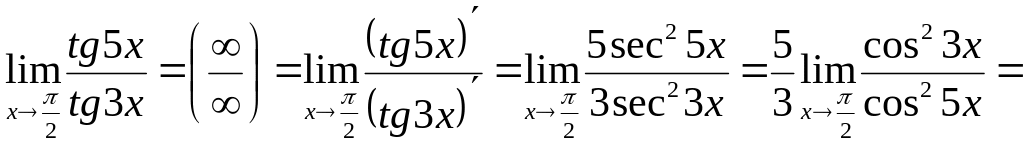
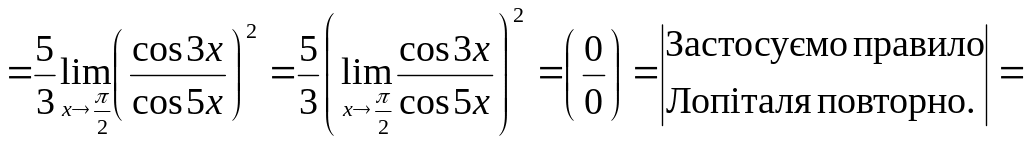
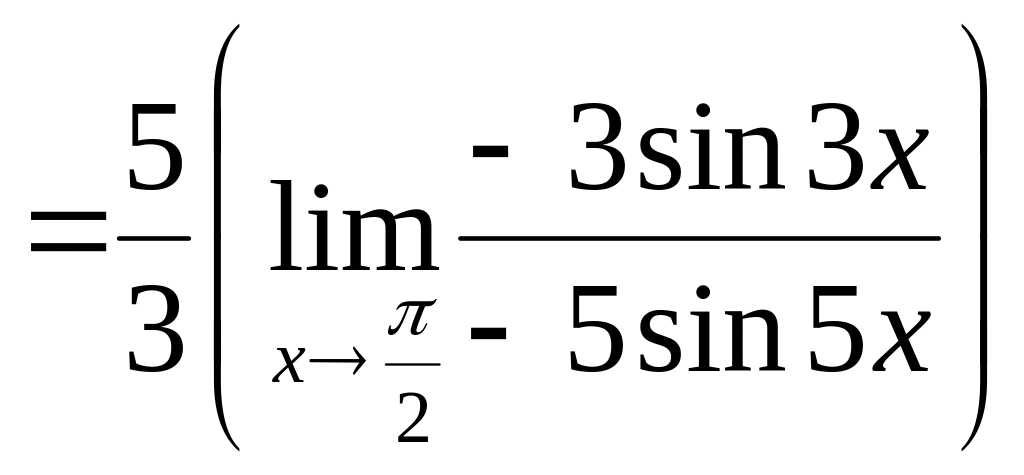
Формула (1) залишається справедливою, коли відношення похідних прямує до нескінченності, тоді і відношення самих функцій також прямує до нескінченності. 8)

Увага! Студент повинен розрізняти поняття «границя дорівнює » та «границя не існує».

Розглянемо два важливих приклади. 9) 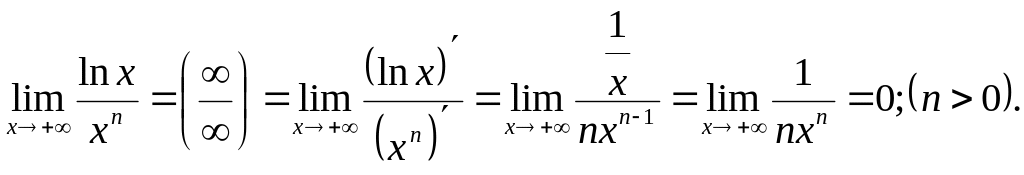10) n – ціле додатне число. Застосуємо правило Лопіталя n разів підряд, дістанемо

Таким чином, коли аргумент прямує до , то степенева функція (n>0) зростає швидше, ніж логарифмічна, а експонента – швидше ніж степенева.

2.3. Розкриття невизначеностей виду та .

Під розкриттям невизначеності виду розуміють знаходження границі якщо і де – це число або .

Під розкриттям невизначеності виду розуміють знаходження границі коли і є нескінченно великі величини одного знаку.

Такі невизначеності з допомогою алгебраїчних перетворень легко зводяться до основних – або . Це можна робити за схемою, умовний запис якої такий:

Знайти границі:

1) В даному випадку має місце невизначеність виду . Записавши функцію як дріб дістанемо невизначеність виду яку розкриємо за правилом Лопіталя:

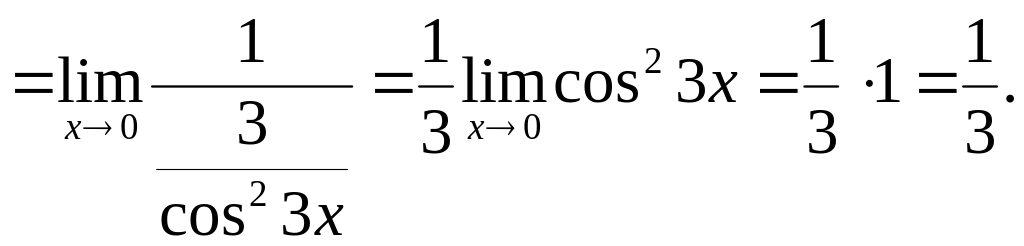
2) Тут невизначеність виду Щоб мати можливість застосовувати правило Лопіталя, запишемо добуток у вигляді частки При чисельник і знаменник цього дробу одночасно прямують до Таким чином, дістали невизначеність виду

3) Так як і при то маємо невизначеність виду . Перетворимо даний вираз так:

4) При маємо невизначеність виду Зведемо її до невизначеності виду

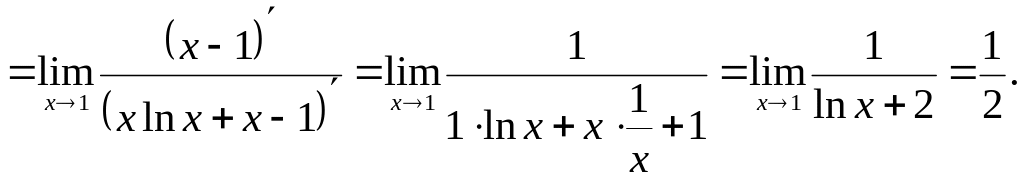
5)

Оскільки

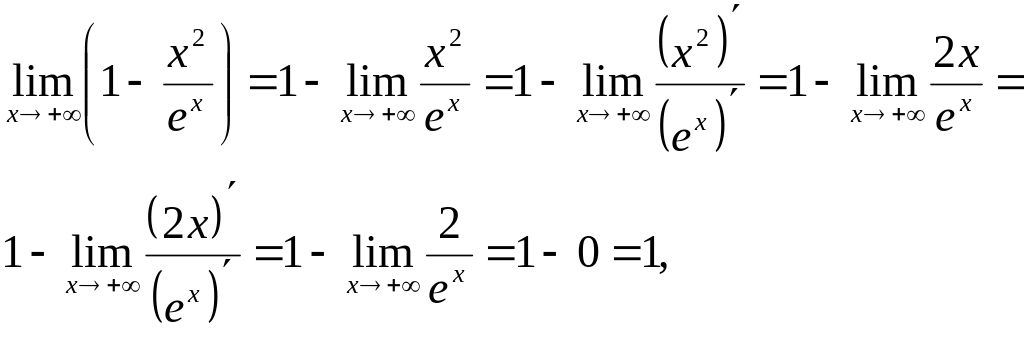
то вихідна границя

2.4. Степеневі невизначеності виду

Такі невизначеності мають місце при розгляді степенево- показникової функції коли f(x) прямує відповідно до а – відповідно до при

Перейдемо від степеневих невизначеностей до невизначеності скориставшись логарифмічною тотожністю яка стосовно степенево-показникової функції набирає вигляду

або

де функція f(x)>0, так як стоїть під знаком логарифма.

Тепер можна записати

Знак границі і знак функції поміняли місцями, що припустимо внаслідок неперервності показникової функції.

Задача звелася до знаходження границі добутку

який є невизначеністю . Нехай ця границя дорівнює А ,тобто

Тоді остаточно для вихідної границі маємо

Знайти вказані границі:

1)

Позначимо через А показник і знайдемо границю:

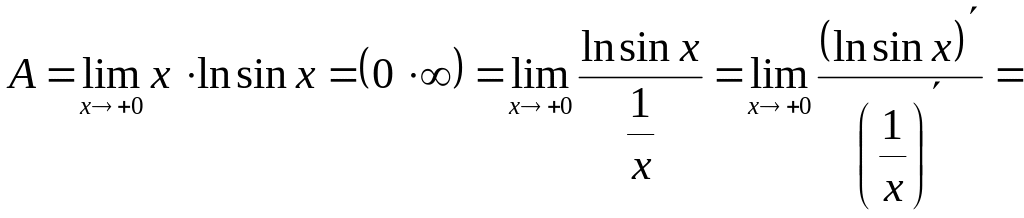
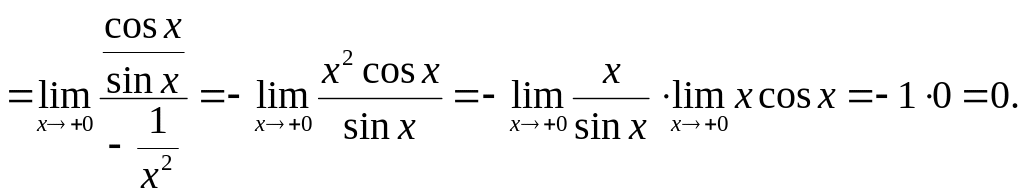
Отже, А=0. Повернемося до вихідної границі.

2)

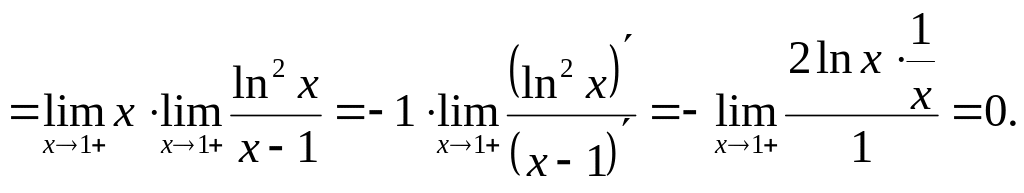
Отже, А=0. В свою чергу, .

3)

.

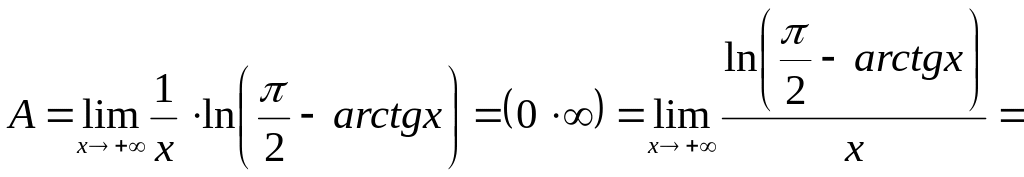
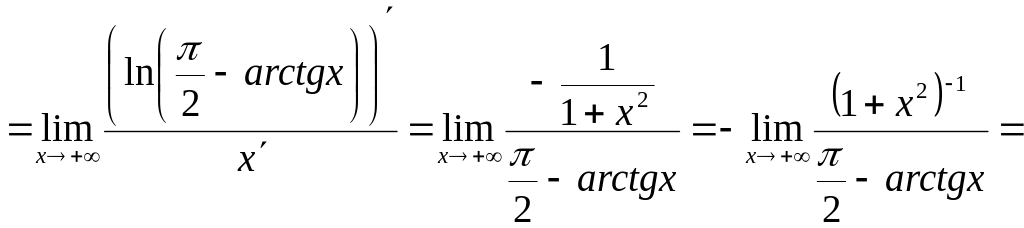
А=0. Остаточно для вихідної границі маємо

4)

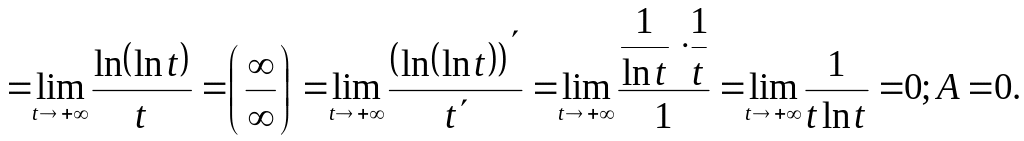
Тепер можна повернутися до вихідної границі:

.

5)

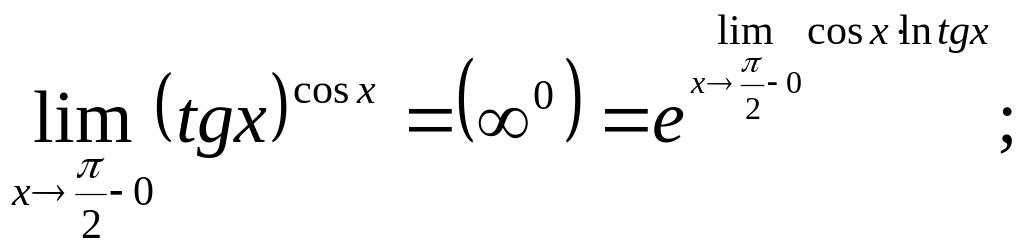
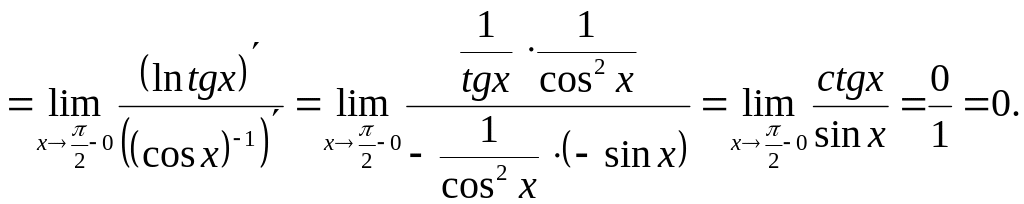
Оскільки А=0, то

6)

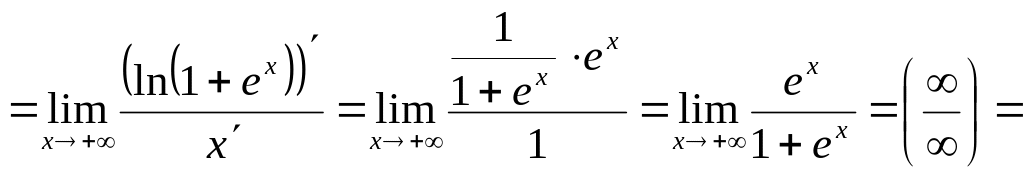
Отже, остаточно дістанемо .

7)

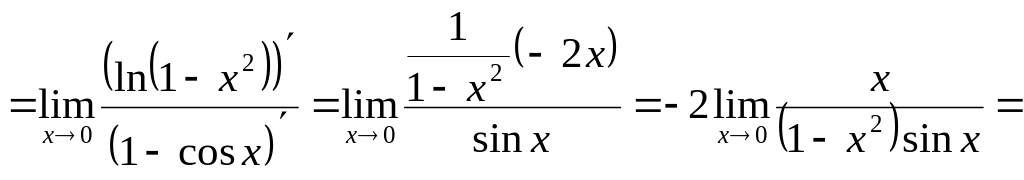
Повертаємося до вихідної границі:

8)

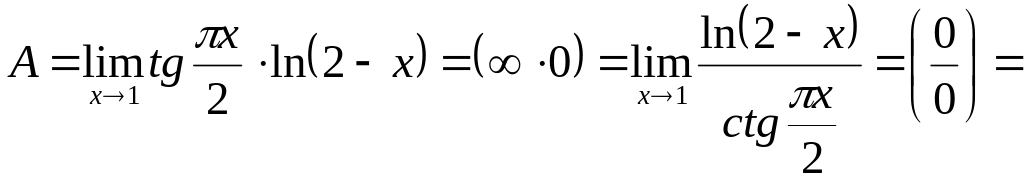
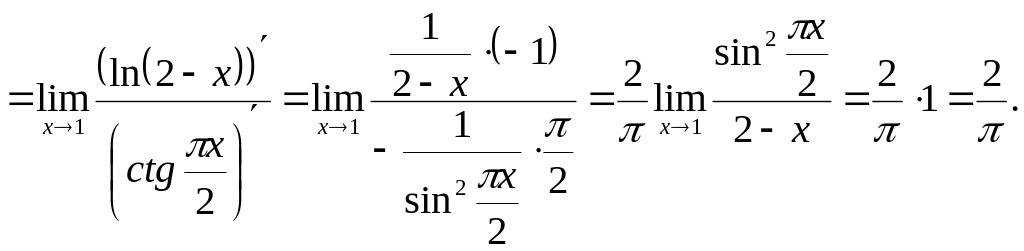
Оскільки то

9)

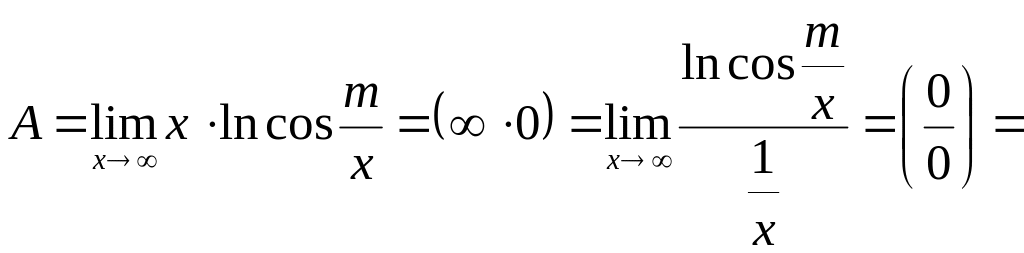
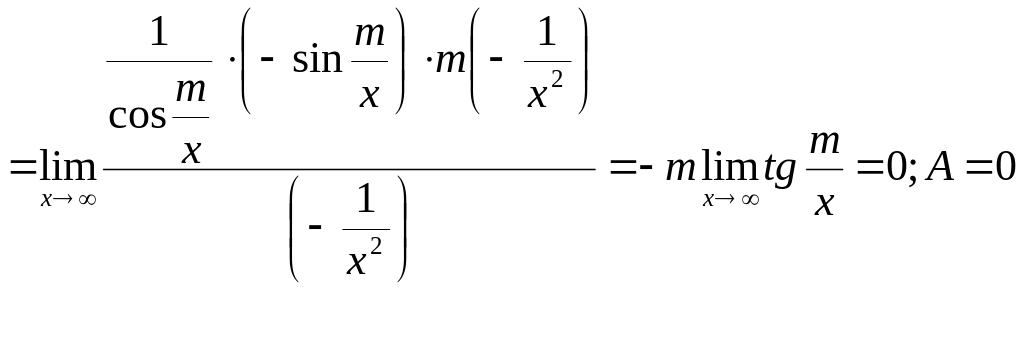
У такому разі .

Зауваження. Можливий ще й такий спосіб розкриття невизначеностей: задану функцію попередньо логарифмуємо і знаходимо границю її логарифма, а потім уже за границею логарифма знаходимо границю самої функції. Покажемо це на прикладі.

Знайдемо границю яку позначимо через В:

Прологарифмувавши обидві частини рівності, будемо мати

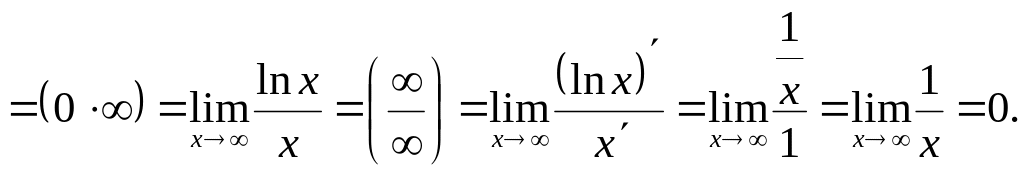
Таким чином, звідки вихідна границя В=1.