
- •Розділ 2. Методи оцінки параметрів розподілів
- •2.1. Предмет і задачі математичної статистики
- •2.2. Варіаційні ряди та їх характеристики
- •2.2.1. Варіаційні ряди
- •2.2.2. Емпірична функція розподілу
- •2.2.3. Графічне представлення варіаційних рядів
- •2.3. Числові характеристики статистичних розподілів
- •2.3.1. Середні величини
- •2.3.2. Показники варіації
- •2.3.3. Моменти розподілу. Характеристики форми розподілу
- •Алгоритм у Mathcad
- •2.4. Статистичні оцінки параметрів розподілів
- •2.4.1. Поняття статистичної оцінки параметрів
- •2.4.2. Точкові оцінки математичного сподівання і дисперсії
- •2.4.3. Методи знаходження оцінок параметрів розподілу
- •2.4.4. Метод моментів
- •2.4.5. Метод максимальної правдоподібності
- •2.4.6. Метод найменших квадратів
- •2.4.7. Метод мінімуму χ2
- •2.5. Методи інтервальної оцінки параметрів розподілів
- •2.5.1. Надійні інтервали
- •2.5.2. Надійний інтервал для математичного сподівання нормального розподілу a при відомому σ
- •2.5.3. Надійний інтервал для математичного сподівання нормального розподілу a при невідомому σ
- •2.5.4. Надійний інтервал для генерального середнього
- •2.5.5. Надійний інтервал для дисперсії нормального розподілу при відомому математичному сподіванні
- •2.5.6. Надійний інтервал для дисперсії нормального розподілу при невідомому математичному сподіванні
- •2.5.7. Оцінка ймовірності біноміального розподілу за частотою
- •Оцінка математичного сподівання
- •2.5.9. Оцінка параметрів гамма-розподілу
- •2.5.10. Інтервальна оцінка параметра розподілу Пуассона
- •2.5.11. Надійний інтервал для різниці середніх нормальних сукупностей при рівних дисперсіях
- •2.5.12. Надійний інтервал для різниці середніх нормальних сукупностей при різних дисперсіях
- •2.5.13. Надійний інтервал для відношення дисперсій нормальних сукупностей
2.5.9. Оцінка параметрів гамма-розподілу
Оцінка параметра λ при відомому β. Математичне сподівання і дисперсія цього розподілу відповідно дорівнюють
![]()
Якщо
![]() то гамма-розподіл співпадає з
експоненціальним, оцінки для якого
розглянуті у попередньому розділі.
Також, як і у випадку експоненціального
розподілу, тут замість параметра
то гамма-розподіл співпадає з
експоненціальним, оцінки для якого
розглянуті у попередньому розділі.
Також, як і у випадку експоненціального
розподілу, тут замість параметра
![]() спочатку оцінюється обернений параметр
спочатку оцінюється обернений параметр
![]() математичне
сподівання.
математичне
сподівання.
Статистична
модель.
Вибірка
одержана
із генеральної
сукупності, яка має гамма-розподіл з
параметрами
![]() і
і
![]() .
Треба побудувати надійний інтервал для
параметра
.
Треба побудувати надійний інтервал для
параметра
![]() .
Розглянемо
спочатку
варіант,
коли параметр
відомий.
.
Розглянемо
спочатку
варіант,
коли параметр
відомий.
Надійний інтервал
будується на основі того факту, що
випадкова величина
![]() ,
де
,
де
![]() точкова
оцінка параметра θ, також має
гамма-розподіл з параметрами
точкова
оцінка параметра θ, також має
гамма-розподіл з параметрами
![]() ,
тобто не залежить від невідомого
параметра θ.
,
тобто не залежить від невідомого
параметра θ.
Алгоритм
побудови надійного інтервалу для
![]()
1. Задаємо початкові
дані моделі:
![]()
2.
Обчислюються точкові оцінки середнього
арифметичного m
і параметра
![]()
![]() .
.
3. Задається рівень
значущості
і визначаються
квантилі гамма-розподілу
![]() ,
відповідно порядків
,
відповідно порядків
![]() ,
де
,
де
![]() –
функція, обернена
до функції гамма-розподілу з
параметрами
–
функція, обернена
до функції гамма-розподілу з
параметрами
![]() ,
,
![]() .
У Mathcad квантилі
.
У Mathcad квантилі
![]() і
і
![]() обчислюються за функцією qgamma(
).
обчислюються за функцією qgamma(
).
4. Обчислюються границі надійного інтервалу для параметра і визначається його надійний інтервал
![]()
5. Обчислюються границі надійного інтервалу для параметра і визначається його надійний інтервал
![]()
Приклад
2.11.
Вибірка об’єму
одержана із генеральної сукупності,
яка має гамма-розподіл з параметрами
![]() Припускаючи, що параметр
Припускаючи, що параметр
![]() відомий –
відомий –
![]() ,
а точне значення параметра
,
а точне значення параметра
![]() невідоме, визначимо надійний інтервал
для математичного
сподівання
невідоме, визначимо надійний інтервал
для математичного
сподівання
![]() і параметра
і параметра
![]() досліджуваної генеральної
сукупності при
рівні значущості
досліджуваної генеральної
сукупності при
рівні значущості
![]()
Розв’язання.
За допомогою
функції Mathcad
rgamma(n,
a) змоделюємо
вибірку об’єму
у припущенні, що генеральна сукупність
має гамма-розподіл з параметром
![]() ,
де
,
де
![]() .
Знаходячи точкову оцінку параметра
.
Знаходячи точкову оцінку параметра
![]() і визначаючи відповідні квантилі
гамма-розподілу, знаходимо надійні
інтервали для параметрів
і визначаючи відповідні квантилі
гамма-розподілу, знаходимо надійні
інтервали для параметрів
![]() .
.
Алгоритм у Mathcad
Початкові дані
![]()
![]()
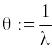
![]()
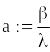
![]()
Моделювання вибірки
із генеральної сукупності, яка має
гамма-розподіл з параметрами
![]()
![]()
Фрагмент вибірки

Вибіркове середнє і дисперсія
![]()
![]()
![]()
Точкові оцінки
параметрів
![]()
![]()
Рівень значущості і відповідні квантилі гамма-розподілу
![]()
![]()
Границі надійного інтервалу для параметра
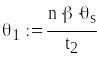
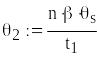
Надійний інтервал для параметра
![]()
![]()
Границі надійного інтервалу для параметра
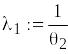
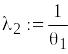
Надійний інтервал для параметра
![]()
![]() ◄
◄
Оцінка параметра β при відомому λ
Статистична модель. Вибірка одержана із генеральної сукупності, яка має гамма-розподіл з параметрами і . Припускається, що параметр відомий, а невідомий. Треба побудувати надійний інтервал для параметра .
Надійний інтервал
будується на основі того факту, що
випадкова величина
![]() де
де
![]() точкова
оцінка параметра
,
також має гамма-розподіл з параметрами
точкова
оцінка параметра
,
також має гамма-розподіл з параметрами
![]() ,
тобто не залежить від невідомого
параметра
.
,
тобто не залежить від невідомого
параметра
.
Алгоритм побудови надійного інтервалу для
1. Обчислюється
точкова оцінка
 .
.
2. Задається рівень значущості .
3. Визначаються
квантилі
![]() ,
де
–
функція, обернена до функції гамма-розподілу
з параметрами
,
де
–
функція, обернена до функції гамма-розподілу
з параметрами
![]() і
і
![]() .
.
4. Обчислюється надійний інтервал з границями:
 .
.
Приклад
2.12.
Вибірка об’єму
одержана із генеральної сукупності,
яка має гамма-розподіл з параметрами
Припускаючи, що параметр
відомий –![]() ,
а точне значення параметра
невідоме, визначимо надійний інтервал
для параметра
при
рівні значущості
,
а точне значення параметра
невідоме, визначимо надійний інтервал
для параметра
при
рівні значущості
Розв’язання.
Моделюємо
вибірку об’єму
у припущенні, що генеральна сукупність
має гамма-розподіл з параметром
,
де
.
Знаходячи точкові оцінки середнього
арифметичного
і параметра
![]() визначаємо відповідні квантилі
гамма-розподілу і знаходимо надійний
інтервал для параметра
визначаємо відповідні квантилі
гамма-розподілу і знаходимо надійний
інтервал для параметра
![]()
Алгоритм у Mathcad
Початкові дані
Моделювання вибірки із генеральної сукупності, яка має гамма-розподіл з параметрами
Фрагмент вибірки

Вибіркове середнє і дисперсія
![]()
![]()
Точкові оцінки параметрів
![]()
Рівень значущості і відповідні квантилі гамма-розподілу
![]()
![]()
Надійний інтервал для параметра
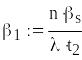
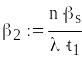
![]()
![]() ◄
◄
Сумісна оцінка параметрів β і λ
Статистична
модель.
Вибірка
одержана
із генеральної
сукупності, яка має гамма-розподіл з
параметрами
![]() і
.
Припускається, що параметри
і
невідомі. Треба за даними вибірки оцінити
невідомі параметри
і
.
Припускається, що параметри
і
невідомі. Треба за даними вибірки оцінити
невідомі параметри
![]()
Алгоритм побудови надійного інтервалу для
Якщо невідомі обидва параметри і , то простого методу одержання їх інтервальних оцінок не існує. Оскільки для даного розподілу
![]() і
і
 ,
,
на основі значень
вибіркового середнього
![]() і вибіркової дисперсії
можна одержати оцінки цих параметрів
у вигляді
і вибіркової дисперсії
можна одержати оцінки цих параметрів
у вигляді
![]()
Згідно з теорією визначення точкових оцінок параметрів розподілів за методом моментів для гамма-розподілу можна також скористатись співвідношеннями
![]() .
.
Із цих співвідношень
для параметрів
![]() знаходимо такі оцінки
знаходимо такі оцінки
![]()
Приклад
2.13.
Вибірка об’єму
одержана із генеральної сукупності,
яка має гамма-розподіл з параметром
(вибірку генеруємо за допомогою функції
![]() ).
Припускаючи, що параметри
невідомі, визначимо надійні інтервали
для цих параметрів при
рівні значущості
).
Припускаючи, що параметри
невідомі, визначимо надійні інтервали
для цих параметрів при
рівні значущості
Розв’язання.
Моделюємо
вибірку об’єму
у припущенні, що генеральна сукупність
має гамма-розподіл з параметром
![]() Знаходячи точкові оцінки середнього
арифметичного параметрів
і відповідні квантилі гамма-розподілу,
знаходимо надійні інтервали для
параметрів
.
Знаходячи точкові оцінки середнього
арифметичного параметрів
і відповідні квантилі гамма-розподілу,
знаходимо надійні інтервали для
параметрів
.
Алгоритм у Mathcad
Початкові дані
Моделювання вибірки
![]()
Фрагмент вибірки

Вибірковi характеристики гамма-розподілу: середнє арифметичне, середнє квадратичне відхилення і другий момент
![]()
![]()
Точкові оцінки параметрів , визначені на основі вибіркового середнього і вибіркового середнього квадратичного відхилення
![]()
Точкові оцінки параметрів , визначені за методом моментів на основі середнього арифметичного і вибіркового другого моменту
![]()
Як показують результати, оцінки параметрів, одержані за цими методами, співпадають. ◄
