Г. Границя функції на плюс або мінус нескінченності

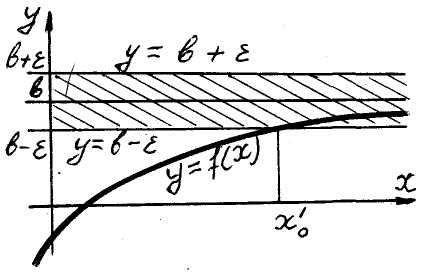
Означення 18. Число називається грани-цею функції при ,

,

якщо для будь-якого існує число таке, Рис. 10 що для всіх значень арґументу, більших від , виконується нерівність

.

Символічно

, якщо .

Геометрично (рис. 10): для таких, що , значення функції лежать в -околі точки b, а відповідна частина її графіка зна-ходиться в заштрихованій смузі між прямими .

Приклад. Довести, що

.

Доведення.

Таким чином,

.

Означення 19. Число називається границею функції при ,

,

якщо для довільного існує число таке, що для Рис. 11 всіх значень арґументу, менших, ніж , виконується нерівність

Символічно

, якщо .

Сформулюйте самостійно, що це означає геометрично (рис. 11).

Приклад. Довести, що

.

Дійсно,

Д. Нескінченно малі (нм)

Означення 20. Функція називається нескінченно малою (нм) в деякому граничному переході, якщо її границя в цьому переході дорівнює ну-лю.

У випадку отримують означення нм з означення 14 при :

функція називається нм у випадку (або в точці ), якщо

Приклад. Функція є нм при ,

,

бо

,

якщо

.

Отже,

.

Приклад. Функція є нм при ,

.

■ , якщо , тобто якщо або ■.

Теорема 3. Всі елементарні функції є нм в своїх ну- Рис. 12 лях.

Доведімо, наприклад, що є нм в точці , тобто

.

■З тригонометричного круга ми бачимо (рис.12), що

sinx< x для 0 < x < і , якщо < x < .

Отже, , якщо , або ж , і ми можемо написати

.■

Теорема 4. Всі наступні функції: a) при ; b) для та при ; c) для і при є нм.

Можна запам"ятати ці факти за допомоги графіків відповідних функцій.

Е. Зв"язок між границями функцій і нескінченно малими

Існує найтісніший зв"язок між границею функції й нескінченно малою в одному й тому ж граничному переході. З"ясуємо його на прикладі границі фун-кції в точці.

Теорема 5. Функція може мати границю b в точці тоді і тільки то-ді, якщо в деякому околі точки її можна зобразити сумою

де (x) – нм при .

■ a) Якщо існує границя

,

тобто

,

то функція є нм при і в .

b) Нехай, навпаки,

f (x) = b + (x),

де (x) – нм при , тобто

.

Звідси на підставі означення границі випливає, що існує границя

.■

Є. Нескінченно великі (нв)

Нехай, наприклад, задано функцію однієї змінної , і x прямує до точки а, .

Означення 21. Функція називається нескінченно великою (нв) при (або – в точці а),

,

якщо для як завгодно великого додатного числа N існує окіл точки а такий, що для будь-якого значення арґументу з проколеного околу виконується не-рівність

.

В символічному запису

.

Зауваження. Якщо функція є нв при , причому вона має тільки додатні (або від"ємні) значення в якомусь околі точки a, то кажуть, що

(відповідно ).

Аналогічно означаються поняття нв при і виокремлюються випадки прямування нв до або .

Приклад. Функція є нв при , причому

.

■ Для як завгодно великого додатного числа N маємо

, якщо , або або ж .

Таким чином,

Зокрема, функція прямує до , якщо x прямує до 0 зліва (при ), і до , якщо x прямує до 0 справа (при ),

,

бо при вона є від"ємною, а при - додатною.■

Приклад. За допомогою тригонометричного круга довести, що

.

■Нехай як завгодно велике, і (див. рис. 13). Тоді для будь-якого з інтервалу

,

виконується нерівність , а це значить, що

.

В більш розгорнутому символічному вигляді ми можемо отриманий результат записати так:

.■

Приклад. Функція є нв, якщо , до того Рис. 13 ж

■Якщо , то (в припущенні, що арґумент x вже став додатним)

для .

Якщо ж , то (припускаючи, що арґумент x вже є від"ємним) маємо

для ■

Теорема 6. Всі наступні функції є нв: a) для ; b) для і ; c) при і ; d) для або ; e) при зліва або справа; g) для зліва і справа. Все це можна запам"ятати за допомогою відомих графіків назва-них функцій.