2.3.3. Правило Лопіталя для розкриття невизначеностей

При обчисленні границь ми вже зустрічалися з невизначеностями типів:

.

Диференціальне числення надає можливість більш простого розкриття принаймні деяких з них.

А. Невизначеності типів

Теорема 5 (правило Бернуллі¹ - Лопіталя²). Границя відношення двох нм або нв (для будь-якого типу граничного переходу) дорівнює границі відношення їх похідних, якщо ця остання існує. Схематично

.

■Ми розглянемо найпростіший випадок, коли , а функції задовольняють умови теореми Коші.

Нехай існує границя

.

Тоді за допомогою теореми Коші отримуємо

оскільки і при .■

Зауваження. Історично склалось так, що правило Бернуллі-Лопіталя зви-чайно називають правилом Лопіталя.

Зауваження. Правило Лопіталя можна (а часто-густо навіть дуже корис-но) комбінувати з іншими методами розкриття невизначеностей. Зокрема, мож-на використовувати таблицю еквівалентних нескінченно малих.

Приклад.

Приклад.

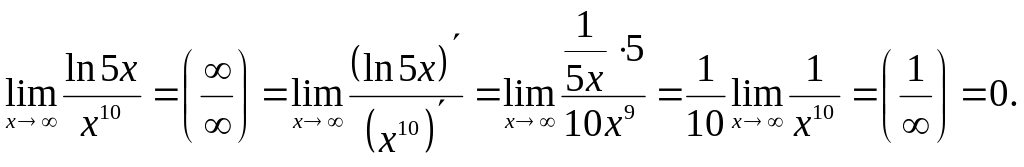
Зауваження. Правило Лопіталя при необхідності можна застосовувати повторно декілька разів.

Приклад. Для будь-якого натурального n

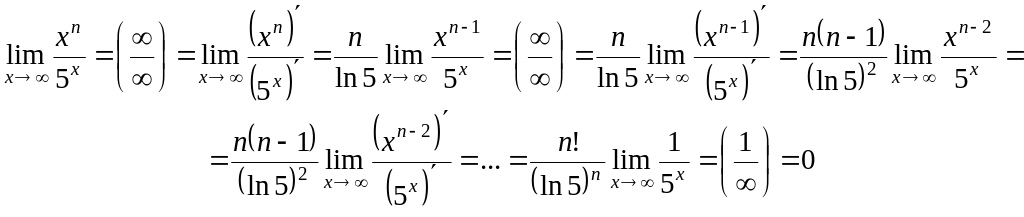Останні два приклади свідчать про те, що степенева функція прямує до нескінченності швидше, ніж логарифмічна, а показникова – швидше степеневої.

Б. Деякі інші типи невизначеностей

Інші невизначеності тими чи іншими перетвореннями треба зводити до перших двох типів.

Не входячи в загальні міркування, обмежимось кількома прикладами.

Приклад.

.

Приклад. Користуючись щойно отриманим результатом, маємо

.

Приклад.

.

2.3.4. Формули Тейлора і Маклорена а. Формули Тейлора і Маклорена для многочлена

Нехай дано многочлен n-го степеня

. ( 6 )

Диференціюючи його n разів, дістаємо

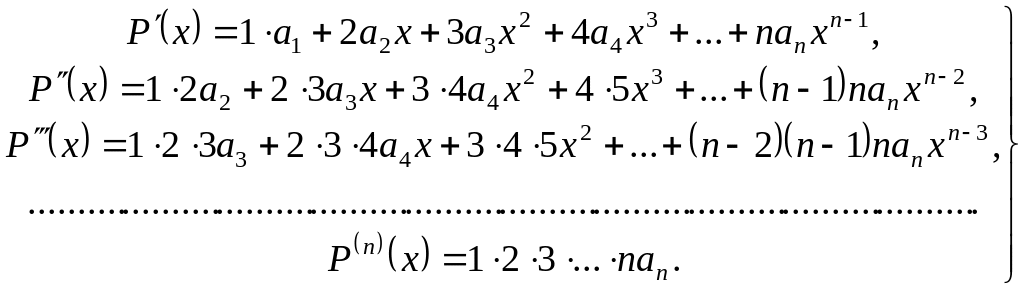( 7 )

Покладаючи в формулах (6), (7) x = 0, ми можемо виразити коефіцієнти многочлена через значення його і всіх його похідних в точці x = 0, саме

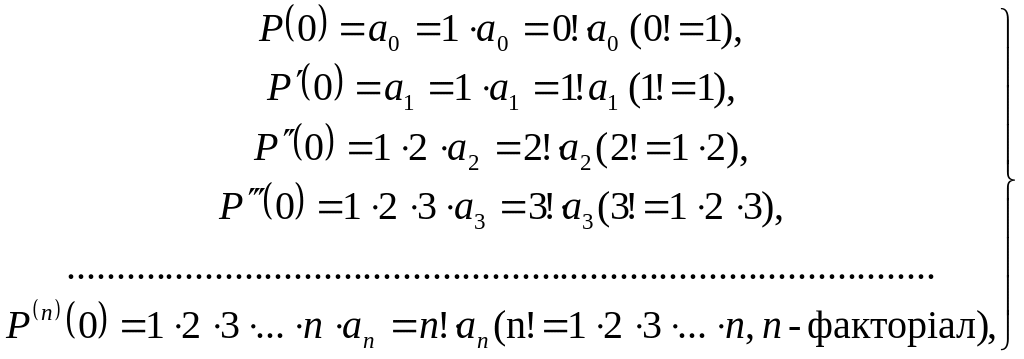
,( 8 )

. ( 9 )

Означення 9. Формула (9) називається формулою Маклорена (або Тейлора¹ - Маклорена²) для многочлена (6). Ми довели наступну теорему.

Теорема 10. Кожний многочлен (6) може бути представлений формулою Маклорена (Тейлора - Маклорена) (9) (з коефіцієнтами (8)).

Якщо многочлен n-го степеня поданий у вигляді розвинення за степенями різниці , саме

, ( 10 )

то тим же шляхом доводиться, що

, ( 11 )

( 12 )

.

Означення 10. Формула (12) називається формулою Тейлора для много-члена (10).

Теорема 11. Кожний многочлен вигляду (10) може бути поданий форму-лою Тейлора (12) (з коефіцієнтами (11)).

Зауваження. Формула Маклорена (9) є частинним випадком формули Тейлора (12) для .

Б. Розвинення бінома (формула бінома Ньютона)

Означення 11. Біномом Ньютона називається наступний вираз

. ( 13 )

Розвинемо біном Ньютона (13) за допомоги формул (6), (9).

( 14 )

Коефіцієнти розвинення (14) (біномні коефіцієнти) позначаються наступним чином:

.

Загалом

( 15 )

Зауваження. Коефіцієнти (15) посідають властивість (доведіть її самостійно)

. ( 16 )

Зауваження. Біномні коефіцієнти можна легко запам"ятати за допомогою так званого трикутника Паскаля¹

1

1 1

1 2 1

1 3 3 1

1 4 6 4 1

1 5 10 10 5 1

…………………………………………………………………

Приклад.