1.1.2. Границя. Нескінченно малі і великі а. Границя функції в точці

Розпочнімо з наступного прикладу.

Приклад. Нехай задано функцію однієї змінної (рис. 4)

з областю визначення , і нехай x прямує до числа 3 (тобто ). Ми бачимо (див. таблицю 1), що відповідні значення функції прямують до числа 6, . Цей факт ми фіксуємо наступними позначеннями

Ми повинні дати точне означення процесу прямування функції до числа.

Table 1

x	2.94	2.96	2.98	3	3.02	3.04	3.06
y = f (x)	5.94	5.96	5.98	Doesn’t exist	6.02	6.04	6.06
	0.06	0.04	0.02		0.02	0.04	0.06

Нехай , а - довільне додатне число, яке ми можемо вважати як зав-годно малим. Розглянемо абсолютну величину різниці між довільними значен-нями функції і числом 6. Матимемо

Наприклад,

,

якщо ;

( ,

якщо і .

Таким чином, для будь-якого додатного як завгодно малого числа існує окіл точки x = 3, тобто інтервал ( на рис. 4), такий, що для довільного , що потрапляє в проколений окіл точки x = 3, тобто = , виконується нерівність

.

Сказане можна висловити символічно таким чином:

Це й є точне означення того факту, що границя нашої функції, якщо x прямує до 3, дорівнює 6, або, що те ж саме, функція прямує до числа 6, якщо її арґу-мент x прямує до числа 3.

Нерівність є еквівалентною наступним співвідношенням (нерівності та включенню)

,

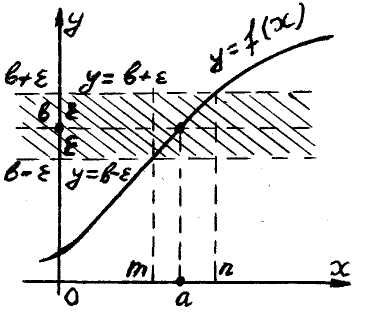
що дозволяє висловити геометричний сенс того факту, що

Рис. 4 (див рис. 4). Саме, якщо x належить проколено-му околу

точки x = 3, то відповідні значення функції знаходяться в -околі точ-ки 6, а відповідна частина її графіка лежить в заштрихованій 2 -смужці, обме-женій прямими

.

На основі розглянутого прикладу ми в змозі дати загальне означення гра-ниці функції , якщо x прямує до якоїсь точки a (або, як часто кажуть, границі функції в точці x = a). Функція може залежати як від однієї, так і від n змінних.

Означення 14. Число b називається границею функції при (границею функції в точці a), або при , якщо для будь-якого додатного як завгодно малого числа існує окіл точки a такий, що для довільного значення x з області визначення функції, яке належить проколеному околу точки a, виконується нерівність

,

або, що те ж саме, подвійна нерівність і включення

.

Символічно,

,

якщо

.

Зауваження.

1) Точка a може належати або не належати області визначення фун-кції . Тому в означенні границі фігурує проколе-ний окіл точки a. Останній можна замінити простим околом , якщо

2) У випадку функції декількох змінних означення границі передбачає можливість прямування x до точки a Рис. 5 вздовж будь-якого шляху, який повністю лежить всере-дині області визначення функції.

3) У випадку n = 1, тобто для функції однієї змінної, неважко встановити геометричний сенс означення границі функції в точці a (рис. 5). Саме, для будь-якого існує окіл точки a (інтервал (m, n) на рис. 5) такий, що для всіх точок , які потрапляють в проколений окіл точки a, значення функції знаходяться в -околі точки , а відповідна частина її графіка лежить в заштрихованій 2 -смузі між прямими , .

4) Означення границі в точці а для функції однієї змінної часто-густо дається в формі, дещо відмінній від викладеної. Саме, окіл точки а припускається симетричним відносно точки. В такому разі його можна подати у вигляді інтервалу довжини і назвати -околом точки .

Оскільки

,

означення границі набуває однієї з двох форм:

якщо

або ж якщо

.

Приклад. Вище ми дали математичне означення того факту, що

.

Зараз ми можемо подати означення в такій формі:

або ж

.

Приклад. Довести на підставі означення границі, що

.

Областю визначення функції є множина всіх дісних чисел. Поведінку функції при показано в таблиці 2.

Table 2

x	1.96	1.97	1.98	1.99	2.00	2.01	2.02	2.03	2.04
	3.84	3.88	3.92	3.96	4.00	4.04	4.08	4.12	4.16
	0.16	0.12	0.08	0.04	0.00	0.04	0.08	0.12	0.16

Нехай > 0 – додатне як завгодно мале число. Тоді

Таким чином, для будь-якого > 0 існує окіл точки x = 2, а саме

= ,

такий, що для всіх значень виконується нерівність

.

За означенням границі (з врахуванням зауваження 1) можемо написати

,

Геометричний сенс розглянутого граничного переходу вста-новіть самостійно.

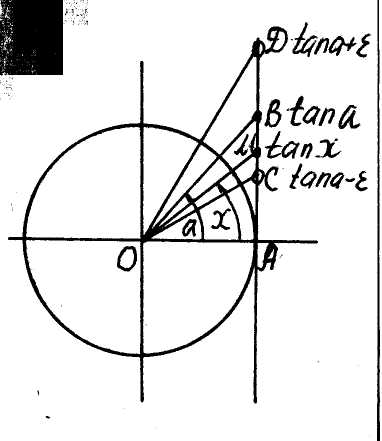
Приклад. За допомогою означення тангенса довести, що для будь-якого

.

Рис. 6 ■Позначимо на лінії тангенсів три точки

(точки C, B, D відповідно, рис. 6) та з"єднаємо ці точки з центром O тригоно-метричного круга. Нехай

(рис. 6).

Отримуємо наступний результат (в символічній формі):

На підставі означення границі маємо ■

Можна поширити цей результат на довільне . Спробуйте зробити це самостійно.

За допомогою означення синуса, косинуса і котангенса (в тригонометрич-ному крузі) можна довести, що

.

Зауваження. Два попередні приклади та названі результати стосовно функцій дають нам перші приклади так званих неперервних функцій, тобто функцій, які посідають властивість вигляду

(границя функції в точці a дорівнює значенню функції в цій точці). Існує багато функцій такого гатунку. Нижче йтиметься про неперервність всіх основних еле-ментарних та елементарних функцій на своїх областях визначення. Але вже за-раз при обчисленні границь ми будемо брати цю неперервність до уваги, при-наймні в простих випадках.

Приклад. Довести, що функція двох змінних

не має границі в початку координат .

■Достатньо показати, що при наближенні до початку координат вздовж деяких двох різних шляхів ми отримуємо різні результати. Як такі шляхи виби-ремо, наприклад, прямі та . Вздовж прямої маємо

, .

а вздовж прямої - зовсім інший результат

, .

На підставі зауваження 2 це значить, що границі функції в початку координат, тобто при , не існує.■

Ми дали означення границі функції однієї або декількох змінних в точці a. Існують і інші типи граничних переходів. Ми коротенько розглянемо їх для функцій однієї змінної .