
- •Міністерство освіти і науки україни донецький національний технічний університет Косолапов ю.Ф. Математичний аналіз першого курсу частини 1 - 2
- •Донецьк 2009
- •Частина перша: вступ до аналізу. Диференціальне числення та його застосування математичний аналіз
- •Підручники
- •Збірники задач
- •1.1.2. Границя. Нескінченно малі і великі а. Границя функції в точці
- •Б. Однобічні границі функції однієї змінної в точці
- •В. Границя числової послідовності
- •Г. Границя функції на плюс або мінус нескінченності
- •Д. Нескінченно малі (нм)
- •Е. Зв"язок між границями функцій і нескінченно малими
- •Є. Нескінченно великі (нв)
- •Ж. Співвідношення між нескінченно великими (нв) і нескінчен-но малими (нм)
- •1.1.3. Властивості границь
- •А. Загальні властивості границь
- •Б. Властивості нескінченно малих
- •В. “Арифметичні” властивості границь
- •Г. Властивості нескінченно великих
- •1.1.4.Стандартні границі а. Перша стандартна границя
- •Б. Друга стандартна границя
- •1. (Третя стандартна границя) ( 3 )
- •2. (Четверта стандартна границя) ( 4 )
- •1.1.5. Відсотки в інвестиціях
- •1.2. Неперервність функцій
- •1.2.1. Неперервність функції в точці а. Основні означення
- •Б. Властивості неперервних функцій
- •В. Точки розриву
- •1.2.2. Властивості функції, неперервної на відрізку або в замкненій обмеженій області
- •1.2.3. Метод інтервалів та його узагальнення
- •2. Диференціальне числення
- •2.1.1. Задачі, які ведуть до поняття похідної а. Швидкість зміни функції
- •Б. Продуктивність праці
- •В. Дотична до кривої
- •2.1.2. Похідна і частинні похідні а. Похідна функції однієї змінної
- •Б. Частинні похідні функції декількох змінних
- •2.1.3. Похідні основних елементарних функцій
- •2.1.4. Диференційовність і неперервність
- •2.1.5. Похідні суми, різниці, добутку, частки
- •1. (Похідна суми і різниці).
- •2. (Похідна добутку).
- •3. (Похідна частки).
- •2.2. Техніка диференціювання
- •2.2.1. Похідна складеної функції
- •2.2.2. Диференціювання неявної, оберненої та параметрично заданої функцій а. Випадок неявної функції
- •Б. Випадок оберненої функції
- •В. Випадок функції, заданої параметрично
- •2.2.3. Похідні вищих порядків
- •2.2.4. Диференціал
- •2.2.5. Похідна за напрямом. Ґрадієнт
- •2.2.6. Похідні в економіці. Еластичність а. Темп зміни функції
- •Б. Граничні величини
- •В. Еластичність функції
- •Властивості еластичності
- •2.3. Основні теореми диференціального числення функцій однієї змінної
- •2.3.1. Теореми Ферма і Ролля
- •2.3.2. Теореми Лагранжа і Коші
- •2.3.3. Правило Лопіталя для розкриття невизначеностей
- •А. Невизначеності типів
- •Б. Деякі інші типи невизначеностей
- •2.3.4. Формули Тейлора і Маклорена а. Формули Тейлора і Маклорена для многочлена
- •Б. Розвинення бінома (формула бінома Ньютона)
- •В. Формули Тейлора і Маклорена для довільної функції однієї змінної
- •Г. Формула Тейлора для функції декількох змінних
- •1. Вступ до математичного аналізу 5
- •1.1. Границя функції 5
- •1.2. Неперервність функцій 43
- •2. Диференціальне числення 60
- •2.2. Техніка диференціювання 71
- •2.3. Основні теореми диференціального числення функцій однієї змінної 97
2.3.2. Теореми Лагранжа і Коші
Теорема 3 (Лагранж1).
Якщо функція![]() :
:
а) неперервна
на відрізку
![]() ;
;
б) має похідну
в інтервалі
![]() ,
,
то існує точка
![]() ,
для якої виконується наступна рівність:
,
для якої виконується наступна рівність:
![]() ,
( 1 )
,
( 1 )
або ж
![]() ( 2 )
( 2 )
■Позначмо
![]() ,
,
звідки
![]() .
( 3 )
.
( 3 )
Замінюючи в (3) b на x, введімо допоміжну функцію
![]() .
( 4 )
.
( 4 )
На підставі зазначених
властивостей функції
функція
![]() задовольняє всі умови теореми Ролля:
вона неперервна на відрізку
,
має похідну
задовольняє всі умови теореми Ролля:
вона неперервна на відрізку
,
має похідну
![]()
в інтервалі
і набуває рівних значень на кінцях
відрізка a, b
(![]() по (4),
по (4),
![]() по (3)). Отже, за теоремою
Ролля існує точка
,
для якої по-хідна
по (3)). Отже, за теоремою
Ролля існує точка
,
для якої по-хідна
![]() ,
тобто
,
тобто
![]() .■
.■
 Геометричний
сенс теореми полягає
в наступному (рис. 5):
якщо графік функції
- неперервна крива, яка має
дотичну в усіх своїх внутрішніх точках,
то існує принаймні одна точка гра-фіка
(
Геометричний
сенс теореми полягає
в наступному (рис. 5):
якщо графік функції
- неперервна крива, яка має
дотичну в усіх своїх внутрішніх точках,
то існує принаймні одна точка гра-фіка
(![]() на рис. 5), в якій дотична до
нього паралель-на хорді
на рис. 5), в якій дотична до
нього паралель-на хорді![]() ,
що з"єднує кінцеві точки
,
що з"єднує кінцеві точки![]() і
і
![]() Рис. 5 графіка.
Рис. 5 графіка.
 Наслідок.
Якщо в умовах теореми Лагранжа
похідна функції
дорівнює нулю,
,
то функція є сталою на відрізку
.
Наслідок.
Якщо в умовах теореми Лагранжа
похідна функції
дорівнює нулю,
,
то функція є сталою на відрізку
.
■Для будь-якої точки
![]() існує точки
існує точки
![]() така, що на підставі формули
(2) мають
така, що на підставі формули
(2) мають
![]() .
.
Звідси випливає, що
![]() .■
Рис. 6 Зауваження.
Обидві умови теореми
Лагранжа, що їх було накладено на функцію
,
є суттєвими для слушності теореми,
зокрема для існування дотичної,
паралельної хорді
.
В іншого боку, ці умови є достатніми,
але не необхідними.
.■
Рис. 6 Зауваження.
Обидві умови теореми
Лагранжа, що їх було накладено на функцію
,
є суттєвими для слушності теореми,
зокрема для існування дотичної,
паралельної хорді
.
В іншого боку, ці умови є достатніми,
але не необхідними.
 Приклад.
Крива, зображена на рис. 6, не
має дотичної, яка була б парале-льною
хорді
.
Ця крива є графіком функції, котра хоч
і неперервна на від-різку
Приклад.
Крива, зображена на рис. 6, не
має дотичної, яка була б парале-льною
хорді
.
Ця крива є графіком функції, котра хоч
і неперервна на від-різку
![]() ,
але не має похідної в (єдиній!) точці
,
але не має похідної в (єдиній!) точці
![]() .
.
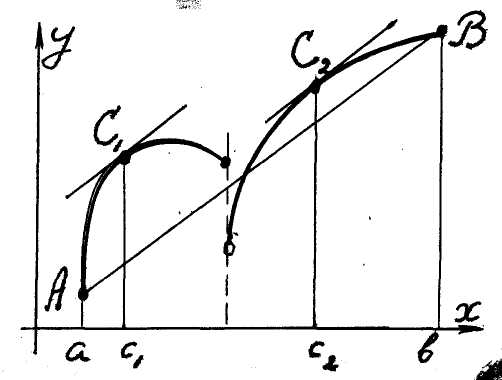
Приклад. Функція, яку графічно подано на рис. 7, не задовольняє умови теореми Лагранжа, але її графік має на-
віть дві дотичні, паралельні
хорді
.
Рис. 7 Приклад.
За допомоги теореми Лагранжа
довести, що для довільних
a, b
таких, що
![]() ,
виконується наступна нерівність:
,
виконується наступна нерівність:
![]() .
.
■Функція
![]() задовольняє умови теореми
Лагранжа для будь-якого відрізка
задовольняє умови теореми
Лагранжа для будь-якого відрізка
![]() ,
а тому існує така точка
,
що
,
а тому існує така точка
,
що
![]() .
( * )
.
( * )
Оскільки
![]() ,
,
легко отримуємо низку вірних нерівностей
![]()
Нарешті з урахуванням (*) маємо
![]()
що і треба було довести.■
Приклад. Довести самостійно, що
a)
![]() для
для
![]() ;
;
b)
![]() для
для
![]() ;
;
c)
![]() для
для
![]() .
.
Приклад. Використовуючи
теорему Лагранжа, знайти наближене
значення числа
![]() .
.
Розв"язок. Нехай
![]() .
.
Теорема Лагранжа стверджує
існування такої точки
![]() ,
що
,
що
![]() .
.
Утворимо далі наступний ланцюжок оцінок:

звідки отримаємо
![]() ,
,
![]() .
.
В останньому запису всі десяткові цифри є вірними.
Приклад. Знайдіть самостійно
наближене значення кореня
![]() .
.
Зауваження. Теорема Лагранжа дозволяє довести достатню умову дифе-ренційовності функції декількох (не менше двох) змінних. Доведімо, наприк-лад, теорему 1 з п. 2.1.4, в якій йдеться про функцію двох змінних.
■Нехай відповідно до умов
теореми функція
![]() має час-тинні похідні в деякому
околі точки
,
які неперервні в самій точці. Запишемо
спочатку повний приріст функції в точці
,
тобто вираз
має час-тинні похідні в деякому
околі точки
,
які неперервні в самій точці. Запишемо
спочатку повний приріст функції в точці
,
тобто вираз
![]() ,
,
в формі
![]()
![]()
Застосуємо тепер теорему Лагранжа до двох різниць в дужках, а саме:
![]()
Внаслідок неперервності частинних похідних в точці можемо напи-сати
![]() ,
,
де
![]() - нм при
- нм при
![]()
Таким чином, маємо
![]()
що і треба було довести.■
Теорема 4 (Коші1).
Якщо функції
![]()
а) неперервні
на відрізку
![]() ;
;
б) мають похідні на інтервалі ;
в) значення
функції![]() на кінцях відрізка не збігаються,
на кінцях відрізка не збігаються,
![]() ,
,
то існує точка , для якої виконується рівність
![]() .
( 5 )
.
( 5 )
Доведіть теорему самостійно, покладаючи
![]()
і вводячи допоміжну
функцію
![]() .
.
