2.2.5. Похідна за напрямом. Ґрадієнт

Нехай деякий напрям (або напрямок) на площині визначено одиничним вектором (ортом)

, ( 29 )

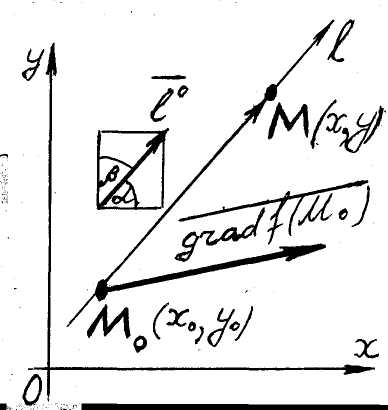а точки такі, що вектор є колінеарним вектору , (див. рис. 2).

Означення 6. Похідною функції двох змінних в точці за напрямом називається (і відповідно позначається) така границя:

. ( 30 )

Зауваження. Крім вислову "за напрямом" можна Рис. 2 використовувати такі: за напрямком, в напрямі, в нап-рямку.

Означення 7. Ґрадієнтом функції двох змінних в точці називається вектор

.( 31 )

Теорема 7. Похідна функції в точці за напрямом дорівнює скалярному добутку значення ґрадієнта функції в цій точці і орта напряму l,

( 32 )

■Нехай , а тому

;

.

Задану функцію можна розглядати як функцію однієї змінної t, а саме:

.

Формула (30) дає, що

,

і тому ми повинні знайти . Але на підставі формули (3)

і отже

.■

З означення скалярного добутку випливає, що похідна (32) за напрямом дорівнює

. ( 33 )

Тому вона набуває найбільшого значення, якщо , тобто якщо похідну функції в точці взято в напрямку ґрадієнта цієї функції в цій же самій точці. Цей факт можна записати наступним чином:

. ( 34 )

Можна сказати, що ґрадієнт функції в точці - це є вектор, який за величиною і за напрямком дає найбільшу швидкість зростання функції в цій точці.

Приклад. Частинні похідні функції по x або y є її похідними в напрямах осей Ox і Oy відповідно.

Приклад. Знайти похідні функції в точці в напряму: a) відомого вектора ; b) ґрадієнта функції в цій же точці ;

c) ґрадієнта функції в точці , відмінній від точки .

Розв"язок. Перш за все

,

і тому

.

Орти вектора і ґрадієнта функції в точці відповідно дорівнюють

.

Отже, на основі формул (32), (34) маємо

Теорема 8. Ґрадієнт є перпендикулярним до лінії рівня функ-ції , яка на площині xOy проходить через точку .

■Нехай лінія рівня (для певного значення C) проходить через точку (рис. 3). Кутовий коефіцієнт дотичної до цієї лінії в точці дорівнює

,

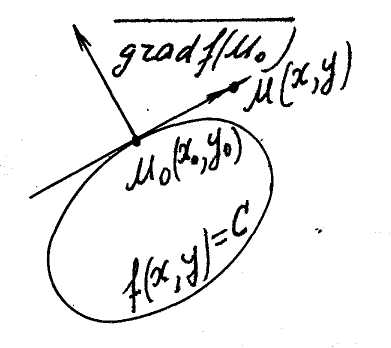звідки отримуємо рівняння дотичної до лінії

, або

.

Звідси випливає, що є Рис. 3 перпендикуляром до лінії рівня l, бо перпендикулярний до напрямного вектора дотичної до l, а саме до вектора .■

Аналогічні означення і факти є справедливими в 3-вимірному просторі для функції трьох змінних , а саме:

, ( 35 )

,

( 36 )

, ( 37 )

. ( 38 )

Теорема 9. Ґрадієнт перпендикулярний до поверхні рівня функції , яка проходить че-рез точку .