2.1.5. Похідні суми, різниці, добутку, частки
Нехай
- дві диференційовні функції змінної x. Тоді похідні їх суми, різниці, добутку і частки обчислюються за такими правилами
1. (Похідна суми і різниці).
2. (Похідна добутку).
3. (Похідна частки).
■Дамо доведення для випадку добутку двох функцій. Зауважимо, що
.
Якщо
то
внаслідок диференційовності, а отже і
неперервності функцій
.
Тому
.■
Частинні випадки.
a)
(сталий множник можна винести за знак диференціювання), бо
.
b)
,
оскільки
.
Приклад. Похідні тангенса і котангенса.
.
.
Приклад. Знайти частинні похідні по x і y функції двох змінних
.
Знаходячи частинну похідну по x (y), ми розглядаємо другу змінну y (відповідно x) як фіксовану (або просто сталу).
Приклад. Продиференціювати функцію (тобто знайти її похідну)
.
.
Приклад. Довести формулу диференціювання добутку трьох функцій.
■
.■
Приклад. Знайти похідну функції
.
На підставі формули, доведеної в попередньому прикладі, маємо
.
2.2. Техніка диференціювання
2.2.1. Похідна складеної функції
Теорема 1. Якщо
функції однієї змінної
диференційов-ні, то
складена функція
має похідну, яка обчислюється
за таким правилом:
( 1 )
або більш коротко
.
■З п. 2.1.4 (теорема 2) випливає,
що функції
неперервні. На цій підставі, якщо приріст
арґументу x
прямує до нуля,
,
то приріст
функції
прямує до нуля,
,
а тому приріст
функції
також прямує до нуля,
.
На підставі формули (14) з п. 2.1.4 можемо записати
,
де
є нм
при
(а отже і при
).
Поділивши обидві частини
рівності на
і переходячи до границі при
,
отримаємо
звідки випливає формула (1). ■
Зауваження. Функцію
часто називають проміжним
арґумен-том, або
внутрішньою функцією,
і ми можемо сформулювати наступне
прави-ло диференціювання складеної
функції: похідна складеної
функції дорівнює до-бутку її похідної
по проміжному арґументу [по
внутрішній функції] і
похідної проміжного арґументу [внутрішньої
функції].
Застосовуючи теорему і
попередні результати щодо диференціювання
основних елементарних функцій (див.
пп. 2.1.3 і 2.1.5), ми можемо скласти наступну
таблицю похідних, в якій
означає деяку функцію.
Таблиця похідних
,
зокрема
,
,
,
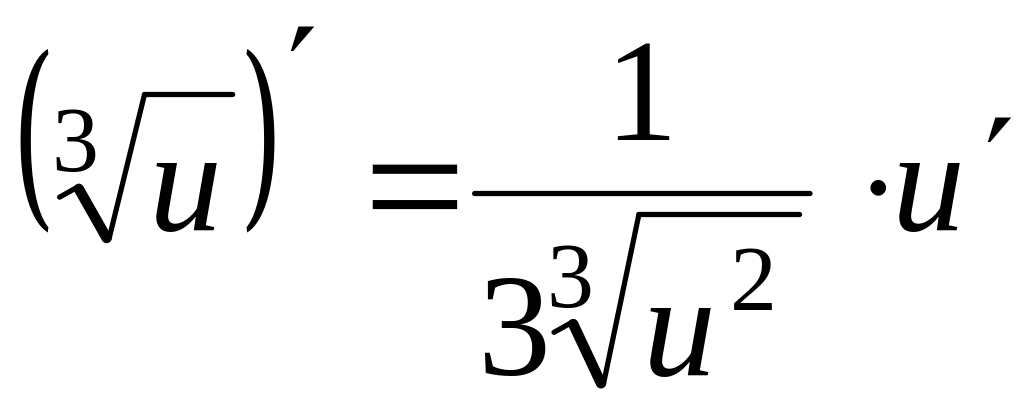зокрема
,
зокрема
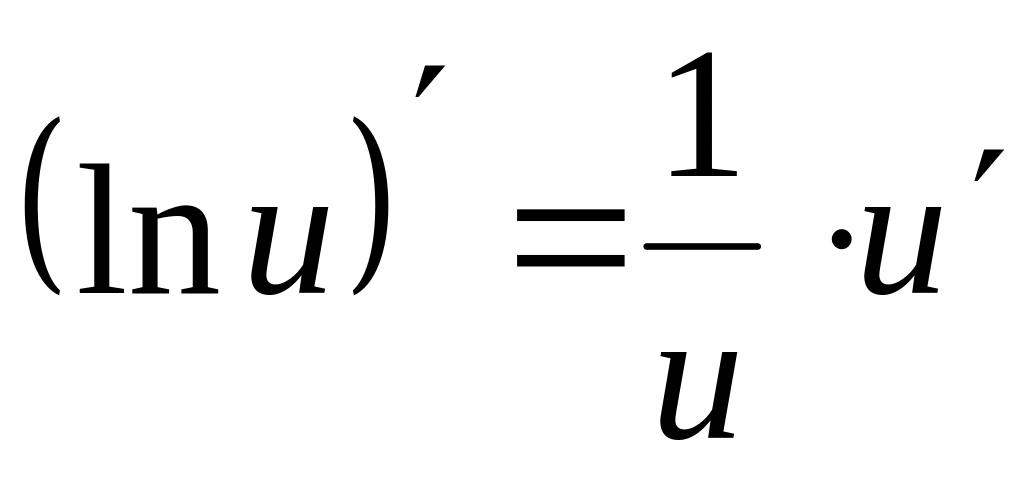
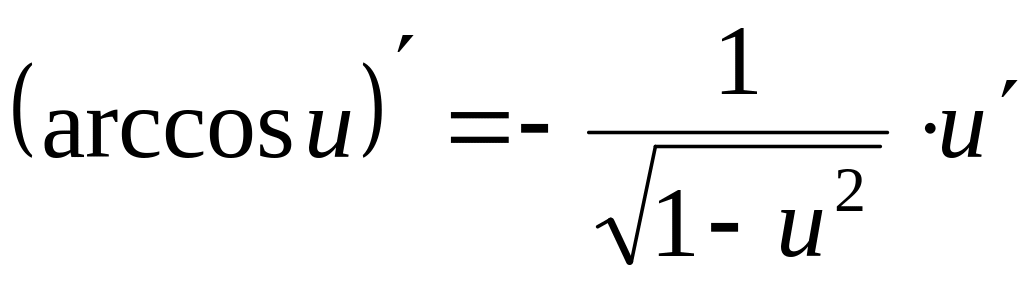
Приклад.
.
Приклад.
.
Приклад.
Приклад. Знайти частинні похідні по x і по y функції двох змінних
.
Вважаючи фіксованим y, знаходимо частинну похідну по x:
.
Фіксуючи тепер x, знаходимо частинну похідну по y:
.
Приклад (логарифмічне диференціювання, або диференціювання за допомоги попереднього логарифмування). Нехай задано функцію
,
( 2 )
яка не є ні степеневою, ні показниковою (іноді її називають степенево-показни-ковою).
Прологарифмуємо ліву і праву частини рівності (2), а потім продиферен-ціюємо отриману рівність почленно (по арґументу x). Використовуючи правила диференціювання складеної функції і добутку, маємо:
Помножаючи тепер обидві частини на
,
знаходимо
,
.
Приклад. Застосуємо цей метод для диференціювання функції
.
Маємо послідовно
.
Метод попереднього логарифмування можна застосовувати не тільки до степенево-показникових функцій вигляду (2), а і в багатьох інших випадках. Як приклад знайдемо цим методом похідну добутку трьох функцій
яку ми вже знаходили в інший спосіб в п. 1.5.
Маємо
.
Для функцій декількох змінних існує безліч аналогічних формул. Одна з них дається наступною теоремою.
Теорема 2. Якщо функції
диференційовні, то існують частинні похідні складеної функції
,
які обчислюються за такими формулами:
.
( 3 )
Доведіть теорему самостійно за допомогою формули (16) з п. 2.1.4 і наступної схеми доведення:
Приклад. Знайти похідну степенево-показникової функції (2)
,
використовуючи формулу на кшталт (3).
Введемо позначення
.
Тоді, перш за все,
.
Першу частинну похідну ми знаходимо як похідну степеневої функції (основа степеня – змінна, а показник степеня - фіксований), а другу – як похідну показникової функції (основа степеня – фіксована, а показник степеня - змінний). Тепер знаходимо похідну складеної функції двох змінних, а саме:
Приклад. Знайти похідну функції
,
використовуючи правило диференціювання складеної функції декількох змінних (без попереднього логарифмування).
Послідовно маємо
.
Приклад. Записати формули для диференціювання складених функцій
( 4 )
Відповідь.
.
( 5 )
Приклад. Знайдімо ще в один спосіб похідну добутку трьох функцій
.
Спочатку знаходимо частинні
похідні функції по
:
.
Тепер за допомоги другої з формул (5) маємо
,
тобто отримуємо той же самий результат, якій вже двічі мали вище.