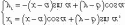Вопрос20. Матрица размеров mxn. Квадратная матрица. Частные случаи (треугольная, диагональная, скалярная, единичная матрицы). Линейные операции над матрицами (сложение и умножение на число) и их свойства. Умножение двух матриц. Свойства операции умножения матриц.

  Любая прямая, перпендикулярная плоскости, называется нормалью к плоскости, а любой ненулевой вектор на такой прямой мы будем называть нормальным вектором плоскости.         

Из определения видно, что нормальный вектор у фиксированной плоскости определяется не однозначно. Все нормальные векторы одной плоскости коллинеарны друг другу и поэтому получаются один из другого умножением на число, отличное от нуля.         

Для того чтобы из параллельных плоскостей выбрать одну, достаточно задать точку, через которую проходит эта плоскость. Итак, если у плоскости известны нормальный вектор и точка, через которую она проходит, то плоскость определена однозначно.

Ур.плоскости через нормальный вектор

Общее уравнение плоскости

  Частные случаи общего уравнения плоскости:

     1) By + Cz + D = 0 - параллельна оси Ox;

     2) Ax + Cz + D = 0 - параллельна оси Oy;

     3) Ax + By + D = 0 - параллельна оси Oz;

     4) Cz + D = 0 - параллельна оси Oxy;

     5) By + D = 0 - параллельна оси Oxz;

     6) Ax + D = 0 - параллельна оси Oyz;

     7) Ax + By + Cz = 0 - проходит через начало координат;

     8) By + Cz = 0 - проходит через ось Ox;

     9) Ax + Cz = 0 - проходит через ось Oy;

     10) Ax + By = 0 - проходит через ось Oz;

     11) z = 0 - плоскость Oxy;

     12) y = 0 - плоскость Oxz;

     13) x = 0 - плоскость Oyz.

Векторное уравнение плоскости

Пусть r -- радиус-вектор текущей точки плоскости ,  -- радиус-вектор точки . Тогда уравнение ( 11.2 ) можно переписать в виде Такое уравнение обычно называют векторным уравнением плоскости

 Взаимное расположение двух плоскостей

     Если , то они:

     1) пересекаются

     2) параллельны (но не совпадают)

     3) совпадают

     Если плоскости заданы уравнениями и то случаи 1 - 3 имеют место, когда:

1. 

     2)

     3)

Вопрос21 Уравнение плоскости, проходящей через данную точку, параллельно 2м неколлинеарным векторам. Уравнение плоскости, проходящей через 3 данные точки. Уравнение плоскости «в отрезках». Нормальное уравнение плоскости.

Уравнение плоскости по точке и двум неколлинеарным векторам

В векторном виде

В координатах

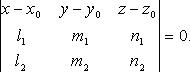
Уравнение плоскости по трем точкам

     В векторном виде

     В координатах

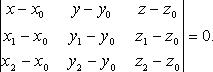
или

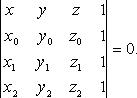
   Уравнение плоскости в отрезках

где a, b, c - величины отрезков, отсекаемых плоскостью на осях координат.

     Нормальное уравнение плоскости

где - углы, образуемые нормальным вектором плоскости с осями координат; p - расстояние от начала координат до плоскости.

     Приведение общего уравнения плоскости к нормальному виду:

Здесь 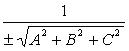- нормирующий множитель плоскости, знак которого выбирается противоположным знаку D, если произвольно, если D = 0.

Вопрос22 Различные виды уравнений прямой в пространстве (параметрические, канонические, через 2 точки, общие) Направляющий вектор прямой, заданной общими уравнениями.

  Уравнения прямой по двум точкам

  Векторно-параметрическое уравнение прямой

где - фиксированная точка, лежащая на прямой; - направляющий вектор.

Канонические уравнения прямой

Вопрос23 Расстояние от точки до плоскости. Взаимное расположение прямой и плоскости. Взаимное расположение 2х прямых в пространстве.

    Взаимное расположение прямой и плоскости

     Плоскость и прямая

     1) пересекаются

     2) прямая лежит в плоскости

     3) параллельны

     Если то случаи 1 - 3 имеют место, когда:

     1)

     2)

     3)

 Расстояние от точки до плоскости

 Взаимное расположение двух прямых

     Если прямые заданы уравнениями и то они:

     1) параллельны (но не совпадают)

     2) совпадают

     3) пересекаются

     4) скрещиваются

     Если то случаи 1 - 4 имеют место, когда ( - знак отрицания условия):

     1)    

     2)    

     3)    

     4)    

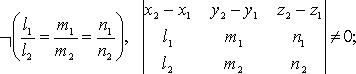
Вопрос 24 поверхности второго порядка (эллипсоид, цилиндры, конус) и их канонически уравнения. Исследование формы поверхности методом параллельных сечений.

 Эллипсоид (рис. 4.18)

     Каноническое уравнение:

     

     

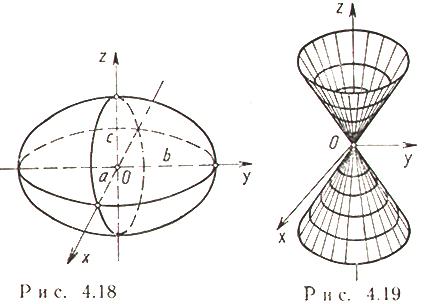
     Конус второй степени (рис. 4.19)

     Каноническое уравнение:

     a = b - конус вращения (прямой круговой).

     Сечения конуса плоскостями: в плоскости, пересекающей все прямолинейные образующие, - эллипс; в плоскости, параллельной одной прямолинейной образующей, - парабола; в плоскости, параллельной двум прямолинейным образующим, - гипербола; в плоскости, проходящей через вершину конуса, - пара пересекающихся прямых или точка (вершина).

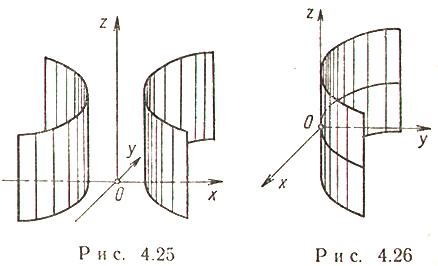
 Эллиптический цилиндр (рис. 4.24)

     Каноническое уравнение:

при a = b - круговой цилиндр.

 Гиперболический цилиндр (рис. 4.25)

     Каноническое уравнение:

     Параболический цилиндр (рис. 4.26)

     Каноническое уравнение:

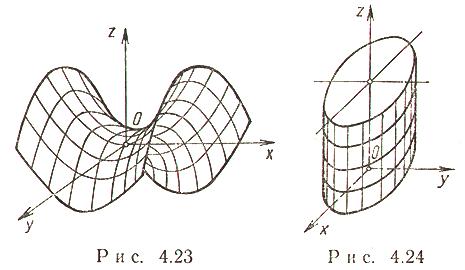
Вопрос25 поверхности второго порядка (гиперболоиды, параболоиды) и их канонические уравнения.

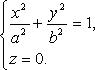
     Асимптотический конус:   

     Сечения однополостного гиперболоида плоскостями - либо эллипс, либо парабола, либо гипербола, либо пара прямых (прямолинейных образующих).

     Эллиптический параболоид (рис. 4.22)

     Каноническое уравнение:

     p = q - параболоид вращения вокруг оси Oz.

     Сечения эллиптического параболоида плоскостями - либо эллипс, либо парабола, либо точка, либо .

Вопрос26 Параллельный сдвиг и поворот декартовой системы координат на плоскости. Формулы перехода от старых к новым и наоборот.

  Параллельный сдвиг координатных осей (рис. 4.8)

     Поворот координатных осей (рис. 4.9)

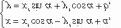
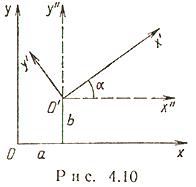
     Параллельный сдвиг и поворот координат осей (рис. 4.10)