
Лекція 1
1. Первісна. Невизначений інтеграл та його властивості План:
Первісна
Невизначений інтеграл та його властивості
Таблиця основних формул та їх застосування
Інтегрування частинами
Інтегрування підстановкою
Українсько-російський словник вжитих в лекції слів, які в мовах мають різне звучання.
Первісна – первообразная Доданок – слагаемое Невизначений інтеграл – – неопределённый интеграл Властивості – свойства Довільна – произвольная Похідна – производная Початкова – начальная Відома – известная Мати – иметь |
Спочатку – сначала Невистачає – недостаёт Застосування –применение Одержимо – получим Звідси – отсюда Зверніть увагу – обратите внимание Обчислення – вычисление Перетворення – –преобразование
|
Напам´ять – наизусть Простежимо – проследим Наважились – осмелились Турбуючись – беспокоясь Заздалегідь бачене – –наперёд виденное Наслідки – последствия Досвід – опыт Добувся корінь – –извлёкся корень Остаточно – окончательно
|
Математичні факти з попередніх розділів, які використовуються в даній лекції.
Без знання напам´ять правил знаходження диференціалів і вміння їх обчислювати для конкретних функцій годі навіть намагатися зрозуміти обчислення первісних та невизначених інтегралів. А тому з чисто формальної сторони з того, що
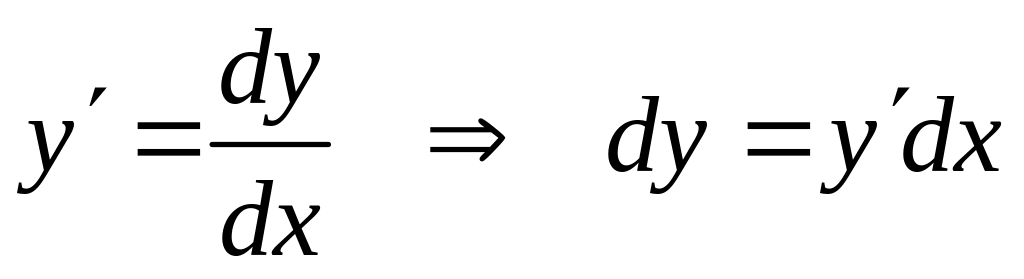 .
.
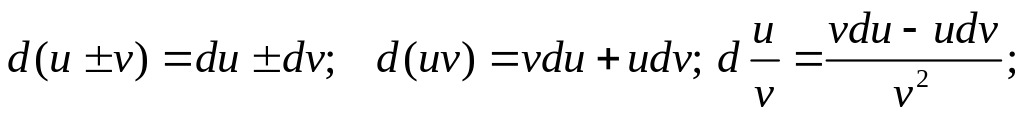
Інваріантність (це іноземне слово означає – незмінність чого-небудь) форми диференціалу полягає в тому, що при
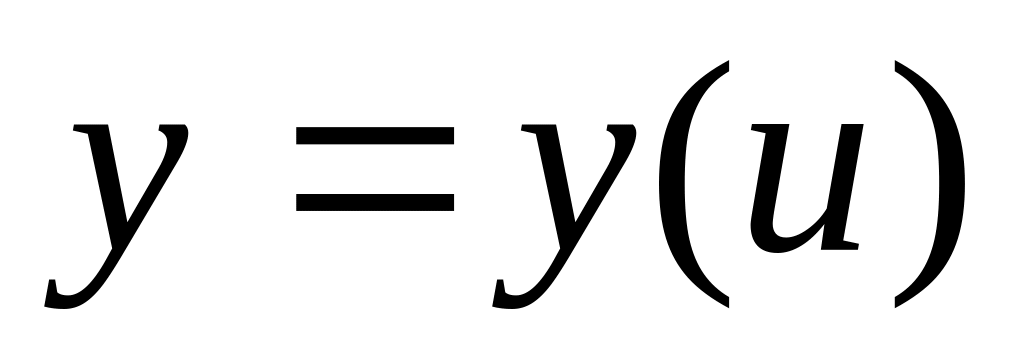 ,
а
,
а
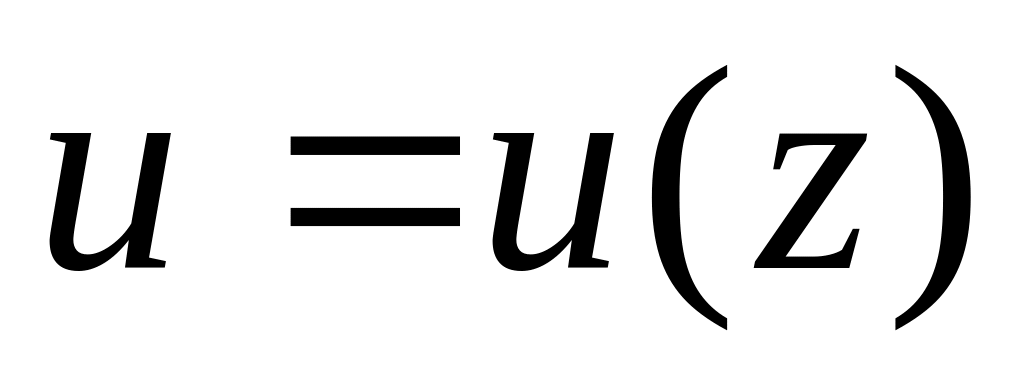 ,
а
,
а
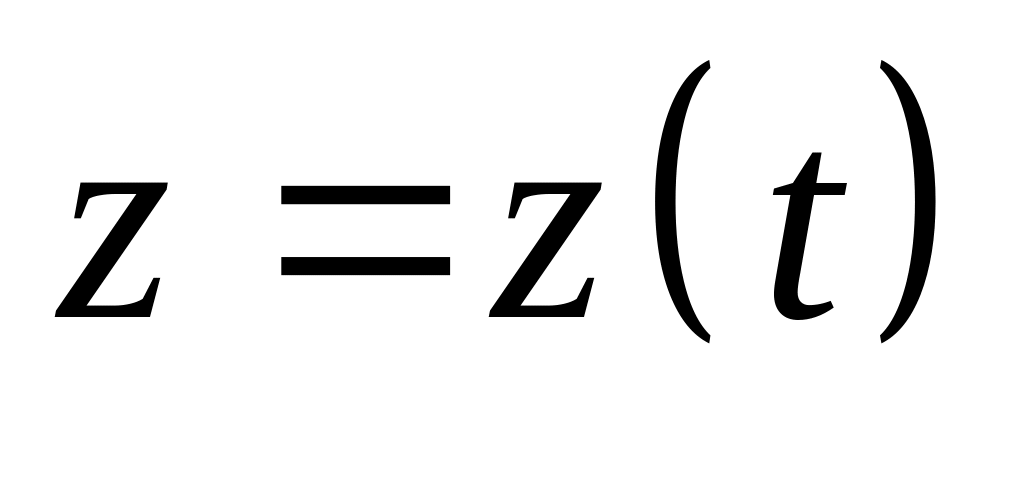 для диференціалу одержимо один і той
же вигляд:
для диференціалу одержимо один і той
же вигляд:
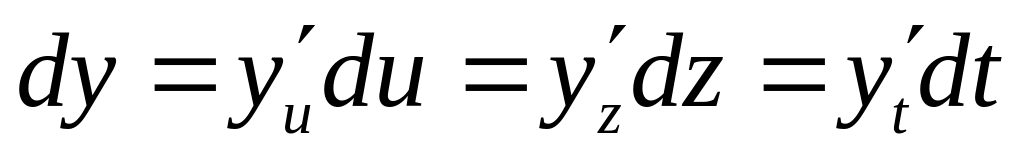 ,
тут
,
тут
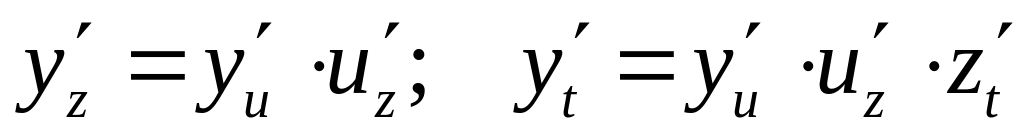 ,
тобто форма першого
диференціала не залежить від того, чи
є аргумент функції незалежною величиною,
чи є в свою чергу функцією другого
аргументу.
,
тобто форма першого
диференціала не залежить від того, чи
є аргумент функції незалежною величиною,
чи є в свою чергу функцією другого
аргументу.
Первісною
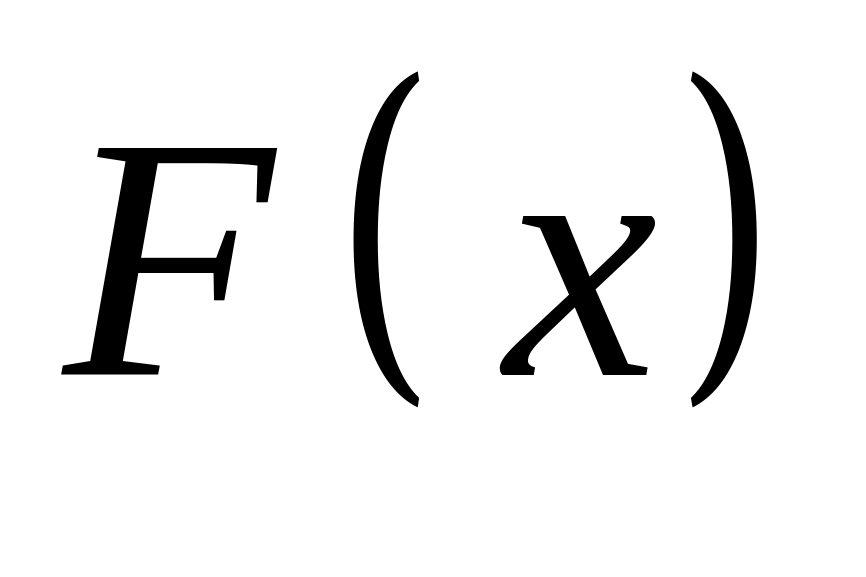 для функції
для функції
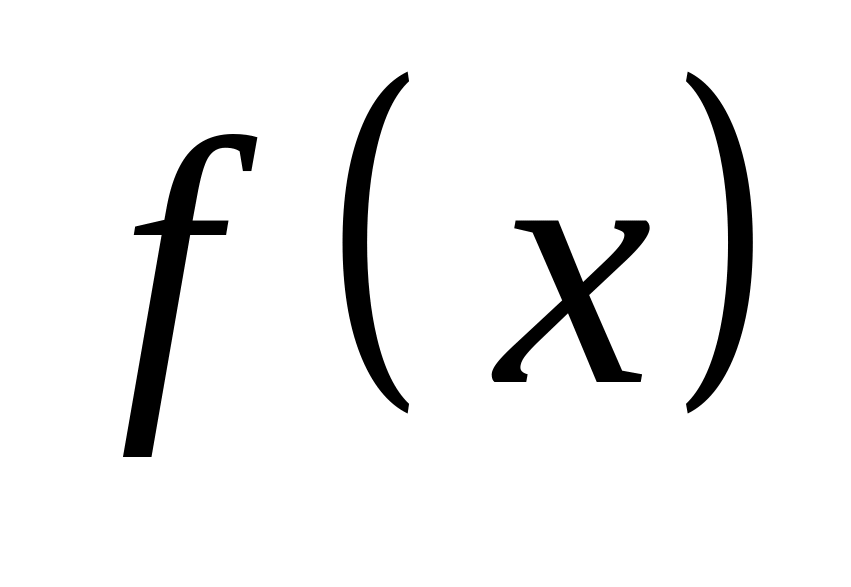 в старших класах школи Ви називали
функцію
тоді, коли виконувалась рівність
в старших класах школи Ви називали
функцію
тоді, коли виконувалась рівність
 .
Слід пригадати три правила знаходженні
первісних:
.
Слід пригадати три правила знаходженні
первісних:
І) якщо
первісна для
,
то
![]() первісна
для
первісна
для
![]() ,
де
,
де
![]() ;
;
2) якщо
![]() первісні відповідно для
первісні відповідно для
![]() ,
то
,
то
![]()
є первісна для
![]() ;
;
3) якщо
первісна для
,
то
![]() первісна
для
первісна
для
![]() ,
де
,
де
![]() ;
;
При інтегруванні доведеться використовувати заміну типу:
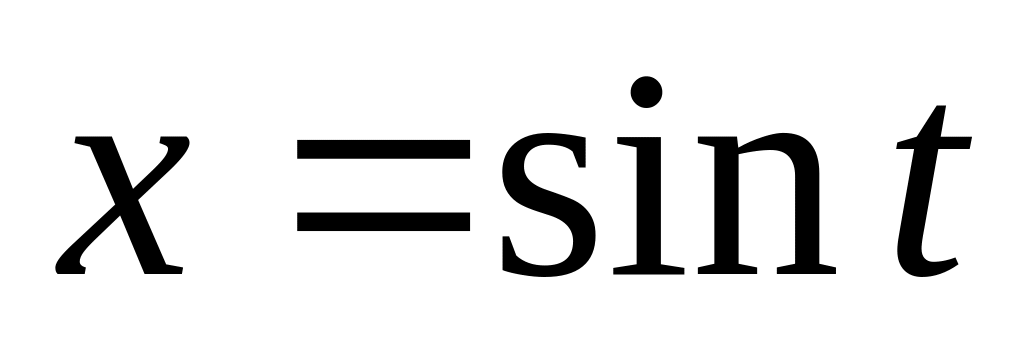 ,
з якої, про- інтегрувавши одержаний
вираз, треба виразити
,
з якої, про- інтегрувавши одержаний
вираз, треба виразити
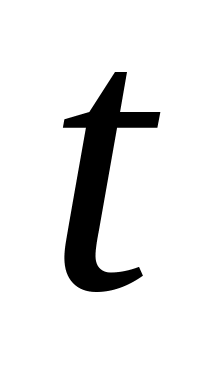 через
через
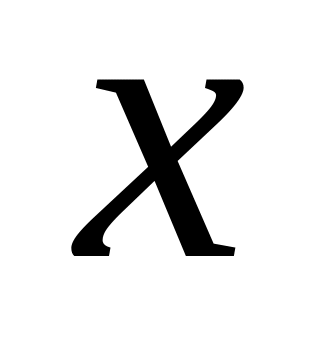 .
Для цього приходиться розв´язувати
найпростіше тригонометричне рівняння
.
Для цього приходиться розв´язувати
найпростіше тригонометричне рівняння
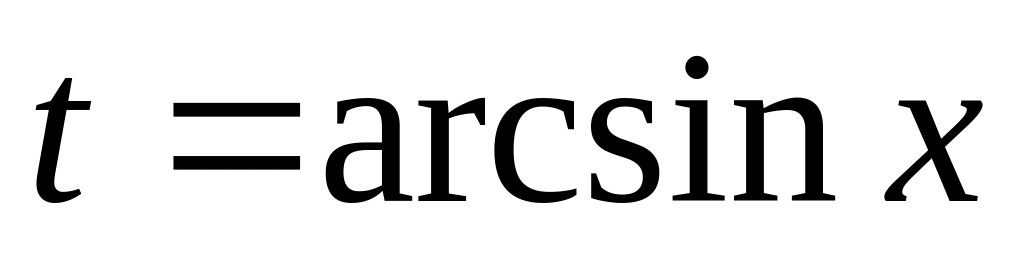 .
Тут ми беремо головне значення арксинуса.
При перетворенні і доведенні
проінтегрованого виразу до відповіді
часто приходиться обчислювати
.
Тут ми беремо головне значення арксинуса.
При перетворенні і доведенні
проінтегрованого виразу до відповіді
часто приходиться обчислювати
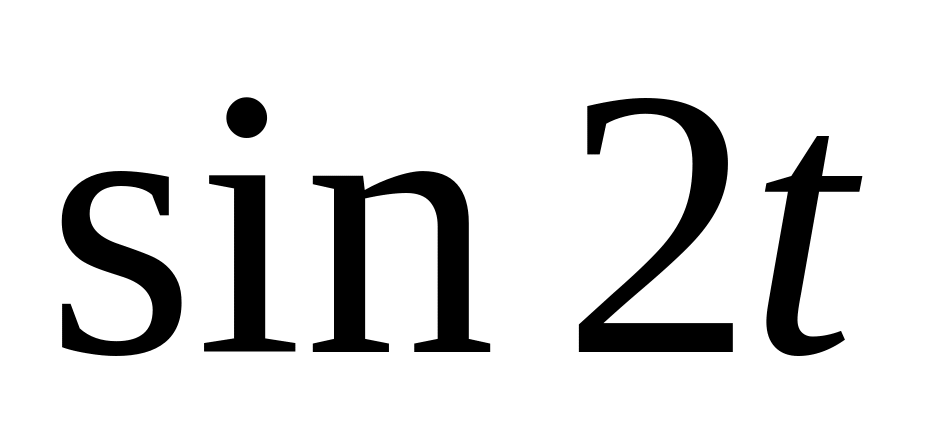 при
відомому
.
Не варто поспішати підставляти і
одержувати
при
відомому
.
Не варто поспішати підставляти і
одержувати
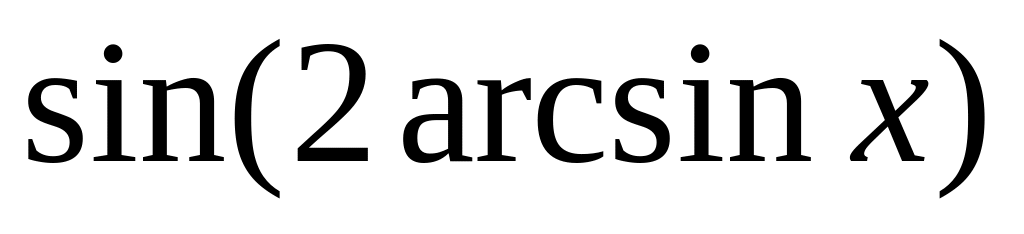 .
Треба робити так:
.
Треба робити так:
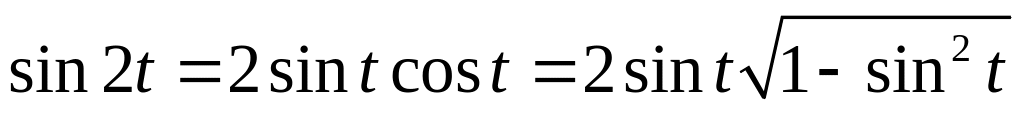 ,
і тепер підставити
,
і тепер підставити
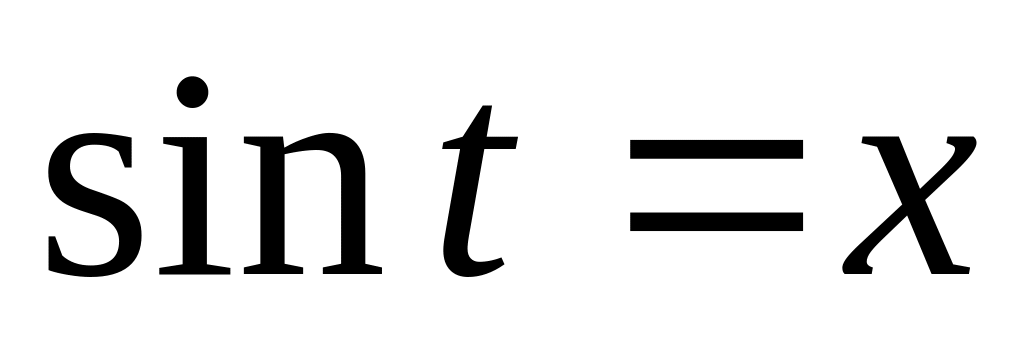 та одержати
та одержати
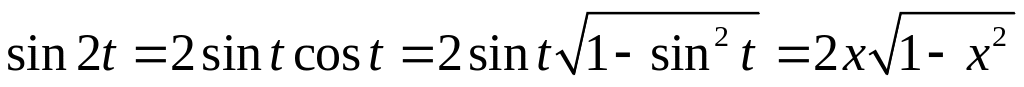 .
.
1.1. Первісна
1.1.1. Постановка задачі знаходження первісної.
Згадаємо свої перші кроки
при вивченні математики і пізнанні
навколишнього світу. Спочатку Вас
навчили додавати два числа. І майже
одночасно ввели операцію обернену до
додавання – операцію віднімання. Далі
таке ж трапилось і при вивченні множення.
Майже одночасно з множенням вам ввели
операцію до нього обернену – операцію
ділення. І саме число обернене до числа
![]() визначили через ділення – 1/n
. Далі у Вас була операція
піднесення до степеня, і операції їй
обернені. У зв’язку з тим, що
визначили через ділення – 1/n
. Далі у Вас була операція
піднесення до степеня, і операції їй
обернені. У зв’язку з тим, що
![]() то таких їх було дві: знаходження кореня
і знаходження логарифму. Світ біполярний:
є тепле і холодне; сухе і мокре; чорне й
біле; позитивне й негативне. Природно
гадати, що і введення операції
диференціювання приведе до їй оберненої
операції, як це було з додаванням,
множенням та піднесенням до степеня.
Так воно і є. А оберненою до диференціювання
операцією є операція знаходження тієї
функції від якої ми знайшли диференціал.
Тобто, якщо у виразі знаходження
диференціала
то таких їх було дві: знаходження кореня
і знаходження логарифму. Світ біполярний:
є тепле і холодне; сухе і мокре; чорне й
біле; позитивне й негативне. Природно
гадати, що і введення операції
диференціювання приведе до їй оберненої
операції, як це було з додаванням,
множенням та піднесенням до степеня.
Так воно і є. А оберненою до диференціювання
операцією є операція знаходження тієї
функції від якої ми знайшли диференціал.
Тобто, якщо у виразі знаходження
диференціала
![]() ми
назвемо функцію
вторинною, то тоді вимушені будемо
функцію із якої ця вторинна функція
одержалась через похідну, назвати
первинною. Але вірно говорити не первинна
а первісна. Переходячи
до образних порівнянь, можна навести
такий приклад. Коли громадянин А йде в
фотоательє і робить там свій фотопортрет
ми
назвемо функцію
вторинною, то тоді вимушені будемо
функцію із якої ця вторинна функція
одержалась через похідну, назвати
первинною. Але вірно говорити не первинна
а первісна. Переходячи
до образних порівнянь, можна навести
такий приклад. Коли громадянин А йде в
фотоательє і робить там свій фотопортрет
![]() ,
то цей фотопортрет ми називаємо похідною
від А, він є похідною від первинного
образу А. Процес пошуку в натовпі самого
громадянина, образ якого (фото) ви
тримаєте перед собою, можна назвати
знаходження первообразу.
,
то цей фотопортрет ми називаємо похідною
від А, він є похідною від первинного
образу А. Процес пошуку в натовпі самого
громадянина, образ якого (фото) ви
тримаєте перед собою, можна назвати
знаходження первообразу.
1.1.2.Означення. Первісною від функції в заданому інтервалі називається функція , похідна від якої дорівнює . Знаходження первісної і похідної від неї можна зобразити у вигляді ходіння по замкненому колу, див. схема 1:
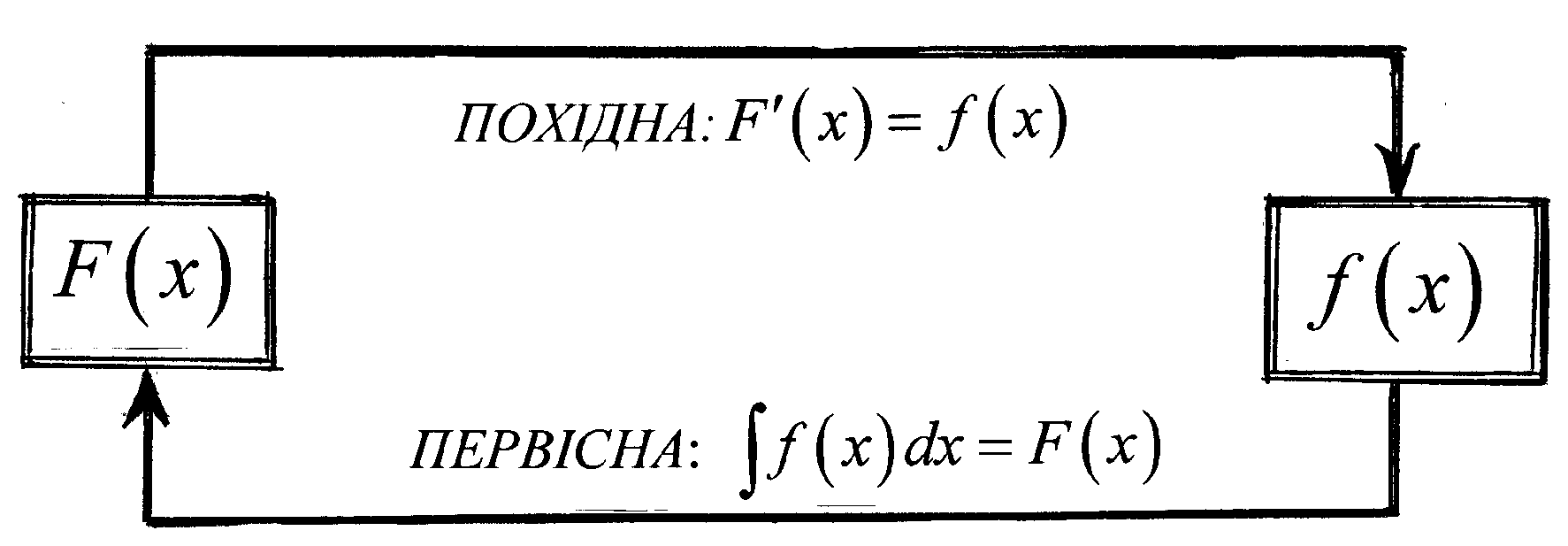
Схема 1.1.
Приклади.
Функція |
Первісна |
Первісна |
Первісна |
|
|
|
|
|
|
|
|
|
|
|
|
1.2.3. Основна теорема про первісні. Яка завгодно неперервна функція має незчисленну множину первісних, причому які завгодно дві з них відрізняються одна від одної лише постійним доданком.
Доведення.
Нехай функція
, буде первісна від функції
.Так
як
![]() , то і функція
, то і функція
![]() також буде первісною від
,
а так як постійна С може приймати яке
завгодно значення, то цим і доводиться,
що первісних буде незчисленна множина.
Покажемо тепер, що які завгодно дві
первісні відрізняються одна від одної
на постійну величину. Нехай
також буде первісною від
,
а так як постійна С може приймати яке
завгодно значення, то цим і доводиться,
що первісних буде незчисленна множина.
Покажемо тепер, що які завгодно дві
первісні відрізняються одна від одної
на постійну величину. Нехай
![]() ,
,
![]() дві первісні від функції
.
Тоді
дві первісні від функції
.
Тоді
![]() ,
,![]() .
Віднімаючи одну рівність від другої
одержимо:
.
Віднімаючи одну рівність від другої
одержимо:
![]() .
Але ж якщо похідна від виразу дорівнює
нулеві, то цей вираз є постійною величиною.
Тобто
.
Але ж якщо похідна від виразу дорівнює
нулеві, то цей вираз є постійною величиною.
Тобто
![]() і ми довели, що дві первісні відрізняються
між собою лише на постійну величину.
і ми довели, що дві первісні відрізняються
між собою лише на постійну величину.
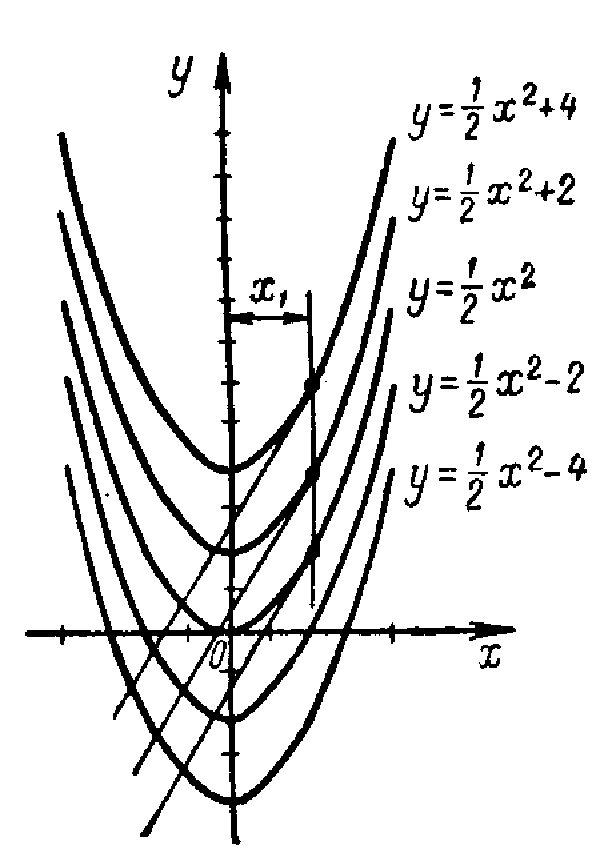
![]() до кривої
,
ми відчуваємо невизначеність положення
цієї кривої на площині хОу. Вона ковзає
вздовж вісі Оу. На рисунку 1.1
зображені декілька інтегральних кривих
до кривої
,
ми відчуваємо невизначеність положення
цієї кривої на площині хОу. Вона ковзає
вздовж вісі Оу. На рисунку 1.1
зображені декілька інтегральних кривих
![]() при
при
![]() .
.
При
![]() дотичні до всіх зображених (і не
зображених) кривих будуть паралельними
і тангенс кута нахилу їх до вісі Ох
дорівнюватиме
.
Очевидно, що рівнянню
дотичні до всіх зображених (і не
зображених) кривих будуть паралельними
і тангенс кута нахилу їх до вісі Ох
дорівнюватиме
.
Очевидно, що рівнянню
![]() на
на
Рис. 1.1. площині хОу буде відповідати множина або, як кажуть, однопараметричне сімейство кривих. С тут виступає параметром.
