2.8 Типи особливих точок

2.8.1 Нулі функції

Нехай функція f(z) є аналітичною в точці z₀. Точка z₀ називається нулем функції f(z) порядку n, якщо виконуються умови

(2.40)

Якщо п=1, то точка z₀ називається простим полюсом.

Точка z₀ тоді і тільки тоді є нулем n-ого порядку функції f(z), яка аналітична в точці z₀, коли в деякому околі цієї точки має місце рівність

, (2.41)

де - аналітична в околі z₀ і .

2.8.2 Ізольовані особливі точки

Точка z₀ називається ізольованою особливою точкою функції f(z), якщо існує окіл цієї точки, в якому f(z) аналітична всюди, крім самої точки z₀.

Точка z₀ називається усувною особливою точкою функції f(z), якщо існує скінченна границя функції f(z) в точці z₀:

. (2.42)

Точка z₀ називається полюсом функції f(z) в точці z₀, якщо

. (2.43)

Для того, щоб точка була полюсом функції , необхідно і достатньо, щоб ця точка була нулем для функції .

Точку називають полюсом n-ого порядку функції , якщо ця точка є нулем n-ого порядку для функції . Якщо п=1, то полюс називається простим.

Для того, щоб точка була полюсом порядку функції , необхідно і достатньо, щоб функцію можна було подати у вигляді

, (2.44)

де функція аналітична в точці і .

Точка називається істотно особливою точкою функції , якщо в точці функція не має границі ні скінченної, ні нескінченної.

Для особливих точок справедливі такі твердження:

1. Для того, щоб точка z₀ була усувною особливою точкою функції f(z), необхідно і достатньо, щоб лоранівський розклад f(z) в околі точки z₀ не містив головної частини.

2. Для того, щоб точка z₀ була полюсом функції f(z), необхідно і достатньо, щоб головна частина лоранівського розкладу f(z) в околі точки z₀ містила скінченне число членів:

, (2.45)

.

Найбільший із показників степеня різниці (z  z₀) в знаменниках членів головної частини ряду Лорана збігається з порядком полюса.

3. Точка z₀ тоді і тільки тоді є істотно особливою точкою для функції f(z), коли головна частина її лоранівського розкладу в околі точки z₀ містить нескінченно багато членів.

2.9 Лишки функції комплексної змінної

Лишком функції w=f(z) в ізольованій особливій точці z=a називається коефіцієнт ряду Лорана цієї функції, який дорівнює

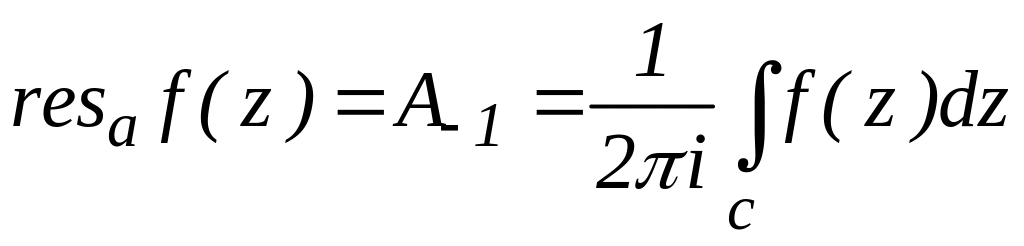, (2.46 )

де с  замкнений контур, який лежить в області аналітичності функції w=f(z), всередині якого лежить точка z=a та інших особливих точок цієї функції немає.

Формули для обчислення лишків:

В простому полюсі:

. (2.47)

Якщо точка є простий полюс функції і функцію в околі точки можна подати як частку двох функцій , причому , , а , то

. (2.48)

В полюсі порядку n:

. (2.49)

Лишок в ізольованій особливій точці дорівнює нулю.

Якщо точка є істотно особливою точкою функції , то для знаходження необхідно знайти коефіцієнт в лоранівському розкладі функції в околі точки ; це буде

Основна теорема про лишки: Якщо функція є аналітичною на межі С області   і неперервною всередині області, за винятком скінченної кількості особливих точок , , ,.., , то

, (2.50)

де С– границя області D.