
- •Лекції з фкз
- •1 Комплексні числа і дії над ними
- •1.1 Алгебраїчна форма
- •1.2 Геометричне зображення.
- •2.2 Нескінченно віддалена точка
- •2 Функції комплексної змінної
- •2.2 Границя функції. Неперервність функції
- •2.3 Основні функції комплексної змінної
- •2.4 Похідна функції комплексної змінної
- •2.4.1 Диференційовність функції. Умови Коші-Рімана
- •2.4.2 Гармонічні функції і їх зв’язок з аналітичними функціями
- •2.5 Інтегрування функції комплексної змінної
- •2.6 Інтегральна формула Коші і її узагальнення
- •2.7 Ряди
- •2.8 Типи особливих точок
- •2.9 Лишки функції комплексної змінної
Лекції з фкз
1 Комплексні числа і дії над ними
1.1 Алгебраїчна форма
Комплексними числами називаються числа виду z = x + iy , де х та у – дійсні числа, а і – уявна одиниця, яка визначена рівностями
![]() або
або
![]() .
.
Числа
![]() ,
,
![]() ,
відповідно, є дійсною та уявною частинами
комплексного числа z.
Два комплексних числа вважаються
рівними, якщо рівні окремо їх дійсні і
уявні частини.
,
відповідно, є дійсною та уявною частинами
комплексного числа z.
Два комплексних числа вважаються
рівними, якщо рівні окремо їх дійсні і
уявні частини.
Алгебраїчні дії над комплексними числами виконуються за формулами:
![]() (1.1)
(1.1)
![]() (1.2)
(1.2)
Множення проводиться за допомогою правила множення двочлена на двочлен.
![]() (1.3)
(1.3)
де
![]() – комплексне число, спряжене до
– комплексне число, спряжене до
![]() .
.
![]() (1.4)
(1.4)
1.2 Геометричне зображення.
Тригонометрична і показникова форми комплексних чисел
Кожне
комплексне число
![]() можна зобразити точкою площини хОу,
яка має координати (х,
у)
(рис. 1.1),
при цьому точки на осі Ох
є дійсними числами. Вісь Оу
називають уявною, а вісь Ох
– дійсною осями. На координатній площині
комплексному числу z
можна поставити у відповідність вектор
можна зобразити точкою площини хОу,
яка має координати (х,
у)
(рис. 1.1),
при цьому точки на осі Ох
є дійсними числами. Вісь Оу
називають уявною, а вісь Ох
– дійсною осями. На координатній площині
комплексному числу z
можна поставити у відповідність вектор
![]() (радіус-вектор точки z), який направлений
з початку координат О
в точку z.
(радіус-вектор точки z), який направлений
з початку координат О
в точку z.
Д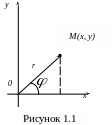 овжину
овжину
![]() цього вектора, тобто відстань від точки
z
до початку координат, називають модулем
комплексного числа z
і позначають
цього вектора, тобто відстань від точки
z
до початку координат, називають модулем
комплексного числа z
і позначають
![]() .
.
Кут
![]() ,
який утворює вектор
,
який утворює вектор
![]() з додатним напрямком осі Ох, називається
аргументом
числа z
і позначається
з додатним напрямком осі Ох, називається
аргументом
числа z
і позначається
![]() . Для аргументу
справедливі формули
. Для аргументу
справедливі формули
![]() ,
y
= sin
,
y
= sin![]() ;
;
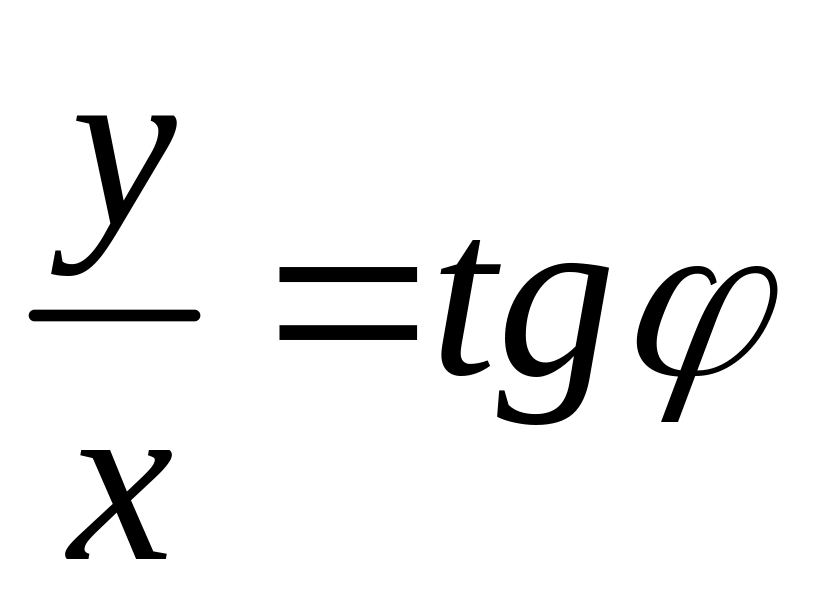 ( r
=
( r
=
![]() ,
,
![]() ) (1.5)
) (1.5)
Значення
![]() визначаються не однозначно, а з точністю
до
визначаються не однозначно, а з точністю
до
![]() k=(0;
k=(0;![]() ...).
...).
Якщо
змінюється в межах
![]() або
або
![]() ,
то виділяють головну частину аргументу,
яка позначається
,
то виділяють головну частину аргументу,
яка позначається
![]() ,
так що
,
так що
![]() ,
(
,
(![]() =0;
=0;![]() …),
де
є головним значенням
…),
де
є головним значенням
![]() ,
яке визначається умовами
,
яке визначається умовами
![]() ,
причому
,
причому
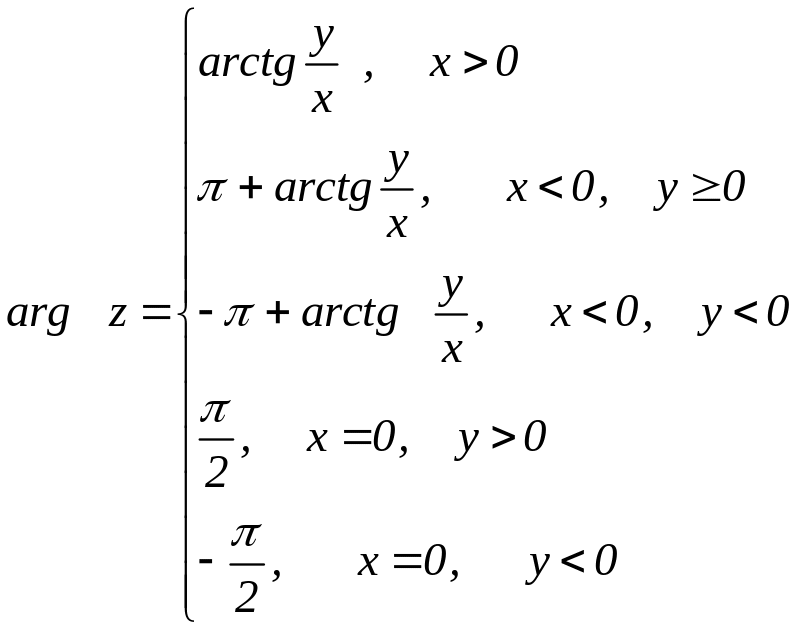 (1.6)
(1.6)
Виходячи з формули для х і у одержимо тригонометричну та показникову форми комплексного числа :
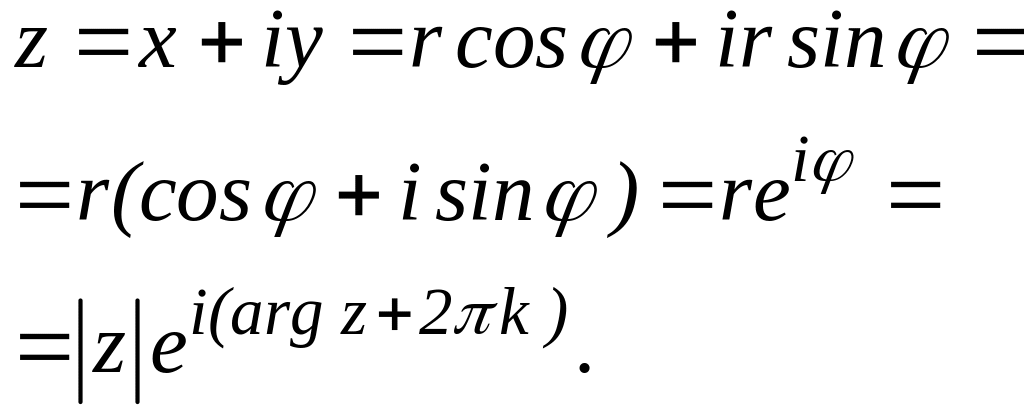 (1.7)
(1.7)
При цьому використали відому формулу Ейлера:
![]() .
.
Для піднесення комплексного числа до степеня n справедлива формула Муавра:
![]() (1.8)
(1.8)
Корені степеня n із комплексних чисел визначаються за формулою:
![]()
![]() (1.9)
(1.9)
де (k =0,1,2,…n-1).
2.2 Нескінченно віддалена точка
В
комплексній площині z
крім скінченних (власних) комплексних
чисел, у яких дійсна і уявна частина
скінченні дійсні числа, додається ще
одне нескінченне (невласне) комплексне
число, позначене символом
![]() .
Це число на комплексній площині називають
нескінченністю або нескінченно віддаленою
точкою.
.
Це число на комплексній площині називають
нескінченністю або нескінченно віддаленою
точкою.
Для нескінченності поняття дійсної і уявної частин, а також поняття аргументу не вводиться (зауважимо, що поняття аргументу не має змісту і для числа 0).
Для
модуля комплексного числа
![]() використовується символ
використовується символ
![]() .
.
Околом
нескінченно віддаленої точки називається
сукупність всіх точок z,
які задовольняють нерівність
![]() (із приєднанням нескінченно віддаленої
точки), тобто сукупність всіх точок z,
які лежать зовні кола із центром в
початку координат досить великого
радіуса R.
(із приєднанням нескінченно віддаленої
точки), тобто сукупність всіх точок z,
які лежать зовні кола із центром в
початку координат досить великого
радіуса R.
Комплексна площина, доповнена числом , називається повною або розширеною комплексною площиною.
2 Функції комплексної змінної
2.1 Визначення функцій комплексної змінної (z = x + iy)
Розглянемо дві площини комплексних чисел: площину z і площину w. Нехай на першій з них задана довільна множина точок Е ( вона може містити і точку z = w).
Означення. Говорять, що на множині Е задана функція w = f(z), якщо кожній точці z із Е поставлено у відповідність одна чи декілька точок w. Е називається множиною визначення функції f(z), а множина К всіх значень w, які f(z) приймає на Е, – множиною зміни функції.
Взявши z = x + iy, w = u + iv одержимо w = f(x + i y) = u(x,y) + iv(x,y), звідки u(x,y) = Re f(z); v(x,y) = Im f(z).
Таким чином, задання функції комплексної змінної рівносильне заданню двох функцій u і v двох дійсних змінних. Про функцію w = f(z) будемо казати, що вона відображає множину Е точок площини z на множину точок площини w. Функцію при цьому називають відображенням.
Якщо
функція w
= f(z)
відображає множину Е
на множину К,
то кожній точці w
із К
відповідає одна чи декілька точок z
із Е.
Таким чином на К
визначена функція
![]() ,
яка називається оберненою стосовно
функції w
= f(z)
і відображає К
на Е.
,
яка називається оберненою стосовно
функції w
= f(z)
і відображає К
на Е.
Нехай функція w = f(z) відображає множину К, а функція w = g(w) відображає множину К на множину Р. Функція w = g (f(z)), яка відображає Е на Р, називається складною функцією, а відображення Е на Р називається накладанням або суперпозицією відображень g і f.
