Лабораторная работа №1 Вычисление алгебраических выражений, производной функции и определенных интегралов

Цель: C помощью панели инструментов Калькулятор интегрированной среды MathCAD научиться вводить формулы, вычислять значения выражения, находить численное значение производной функции в заданной точке. Научиться находить определенные интегралы функций.

Задание 1: Средствами MathCAD вычислить:

при a = 0,124, b = 1,14, x = 2,125.

Методика выполнения задания:

Начальные значения переменных a, b, x зададим обычным присваиванием определенных значений с помощью кнопки на панели инструментов Калькулятор или с клавиатуры, набрав : (двоеточие). Искомой переменной у присвоим заданное выражение. Набирая формулу, будем пользоваться шаблонами необходимых функций на панели инструментов Калькулятор (рис.). Если шаблон какой-либо функции отсутствует на данной панели, вызовем ее с помощью команды Вставка→Функция или с помощью кнопки Вставить функцию на панели инструментов Стандартная.

Рис. Панель инструментов Калькулятор

Для вывода результата наберем с клавиатуры y= , результат появится автоматически на экране как на рис.

Рис. Пример вычисления значения выражения

Варианты индивидуальных заданий

Вычислить значение выражения

№В	Выражение
1	; а=0.83, х=1.2
2	; а=0.12, х=0.36
3	; a=0.394, b=0.124, x=0.842
4	; a=0.343, x=0.834
5	; a=0.334, x=1.256
6	; x=0.104, a=4.213
7	; x=0.117, a=2.346
8	; =0.2, x=0.114
9	; x=2.512, a=0.135
10	; x=2.126, b=2.438, a=0.324
11	; x=0.834, b=0.242, a=0.125
12	; a=0.344, x=0.125
13	; a=2.124, b=0.835, a=0.54
14	; a=0.344, b=1.124, x=0.455
15	; x=0.117, a=0.832
16	; a=0.124, b=0.338, x=0.817
17	; a=0.274, b=0.392, x=0.736
18	; b=0.614, a=0.125, x=1.23
19	; a=0.834, b=1.242, x=0.127
20	; x=2.568, a=0.825, b=0.144
21	; x=0.121, a=2.125
22	; x=0.456, a=1.256, b=0.122
23	; x=0.156, b=1.255
24	; x=0.636, a=0.214, b=0.122
25	; x=0.321, a=1.201
26	; a=2.126, b=2.121, x=0.344
27	; a=3.242, x=0.124
28	; x=0.124, b=3.184, a=0.647
29	; x=0.124, b=2.347, a=0.794
30	; x=0.346, a=2.124, b=0.514

Задание 2. Средствами MathCAD найти производную функции в точке х=1.

Методика выполнения задания:

Для того чтобы найти производную функции и вычислить ее численное значение, необходимо сделать следующее: Сначала определим точку, в которой необходимо найти производную. Щелкнем ниже определения этой точки. Для вычисления производной используем кнопку на панели Калькулус . Появится оператор производной с двумя полями. На поле в знаменателе и наберем имя переменной, по которой проводится дифференцирование - х. На поле справа от наберем выражение, которое нужно дифференцировать. Чтобы увидеть результат, нажмем знак = (рис. ().

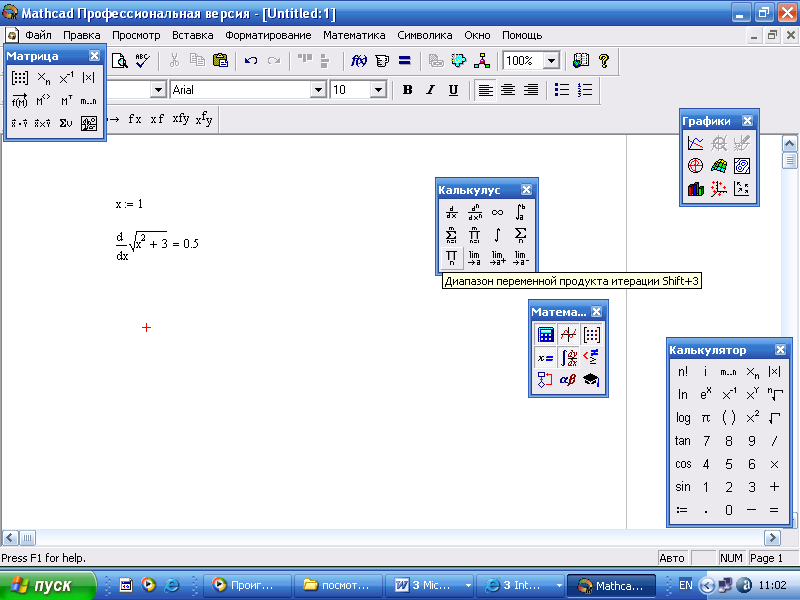Рис. Вычисление производной функции в точке

Варианты индивидуальных заданий

Средствами MathCAD найти производную функции f(x) в заданной точке x=1.

№В	f(x)	№В	f(x)
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Задание 3.

Средствами MathCAD найти определенный интеграл функции .

Методика выполнения задания:

Оператор интегрирования в Mathcad предназначен для численного вычисления определенного интеграла функции по некоторому интервалу.

Для того, чтобы вычислить определенный интеграл, необходимо сделать следующее: Щелкнем кнопку на панели Калькулус. Появится знак интеграла с пустыми полями для подынтегрального выражения, пределов интегрирования и переменной интегрирования. На поле внизу и наберем нижний предел интегрирования, на верхнем поле – верхний предел интегрирования.Щелкнем на поле между знаком интеграла и d и наберем выражение, которое нужно интегрировать. На последнем пустом поле наберем переменную интегрирования – х. Чтобы увидеть результат, нажмем знак = (рис().

Рис. Вычисление определенного интеграла

Варианты индивидуальных заданий

Средствами MathCAD найти определенный интеграл функции f(x) на заданном интервале [0;4].

№В	Вариант задания	№В	Вариант задания
1		16
2		17
3		18
4		19
5		20
6		21
7		22
8		23
9		24
10		25
11		26
12		27
13		28
14		29
15		30

Задание 4:

Построить графики функций и , при изменении х от -10 до +10 с шагом 0,5.

Методика выполнения задания:

MathCAD позволяет строить самые разнообразные графики: в декартовой и в полярной системе координат, с масштабной сеткой и без неё, с линейным и логарифмическим масштабом, с отметкой линий прямоугольниками, крестами, ромбами и т.д. Для визуального отображения различных зависимостей используют семь видов графиков. Типов графиков в MathCAD, конечно, намного больше, но на панели инструментов имеется ровно семь кнопок для создания семи типов графиков.

Самый распространенный график: двухмерный декартов график (X-Y Plot), иллюстрирующий связи между двумя или несколькими векторами.

Декартов график строится, как правило, в два шага:

1. задание вида функций одной переменной, например ;

2. построение графика.

Построение графика осуществляется следующим образом:

1. Установите курсор на рабочем поле и введите с клавиатуры: f(x):=-4/x.

2. Формирование вектора значений: введите с клавиатуры: х:10;10. При такой записи шаг изменения аргумента берется по умолчанию равным 1. Если такая точность не устраивает пользователя, то указывается первое (минимальное) значение аргумента, затем через запятую − второе значение аргумента, равное первому значению плюс шаг, а затем после нажатия клавиши точка с запятой (;) верхний предел диапазона изменения аргумента х. Так, для задания шага изменения аргумента равного 0.5, необходимо набрать х:-10,-9.5;10.

3. Построение графика начинается с вывода на экран дисплея заготовки графика − двух вложенных прямоугольников с черными квадратиками у левой и нижней сторон: щелкните на кнопке Графики панели инструментов, в данном случае .

4. Заполните заготовку графика именем функции и именем аргумента:

− щелчком мыши установите курсор в точку Функция f(x) − черный квадратик у левой стороны прямоугольника;

− наберите f(x);

− щелчком мыши установите курсор в точку Аргумент Х − черный квадратик у нижней стороны прямоугольника;

− наберите х, нажмите <Enter> (рис.).

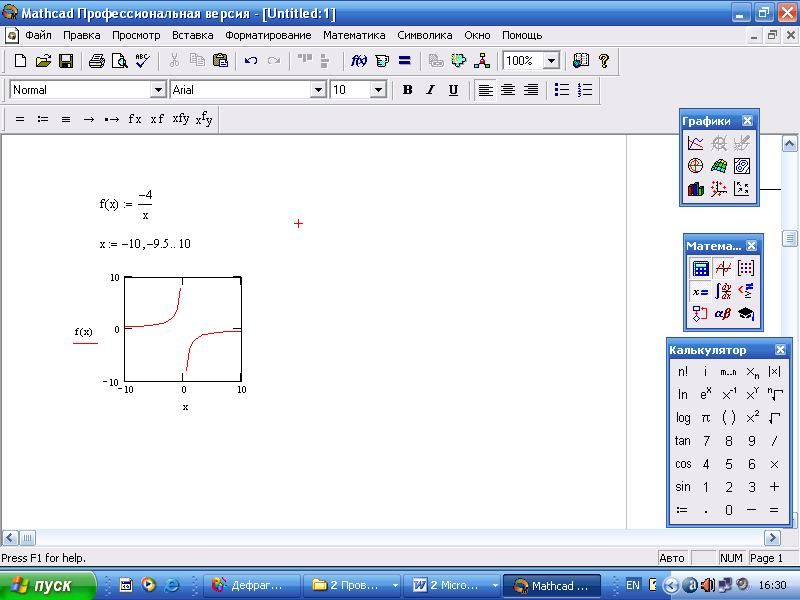
Рис. Автоматически построенный

график

4. Для оформления графика координатными осями выполните следующее:

− дважды щелкните мышью на графике − появится диалоговое окно Formatting Currently Selected X-Y Plot;

− выберите вкладку X-Y Axes;

− в поле выбора Axes Style нажмите Crossed для представления графика с изображением осей координат;

− в поле X-Axis уберите флажок Auto Grid, в поле ввода Number of Grids введите число 5, что означает разметку оси Х;

− в поле Y-Axis уберите флажок Auto Grid, в поле ввода Number of Grids введите число 4;

− измененный график появится на экране.

4. Чтобы модернизировать график, выполните следующие шаги:

− установите курсор на графике и двумя щелчками мыши вызовите диалоговое окно Formatting Currently Selected X-Y Plot;

− в диалоговом окне выберите вкладку Traces;

− в однострочном поле Color установите цвет grn (зеленый);

− в однострочном поле Type установите bar (прямоугольник);

− нажмите клавишу <ОК>, на экране появится новое представление графика (рис.).

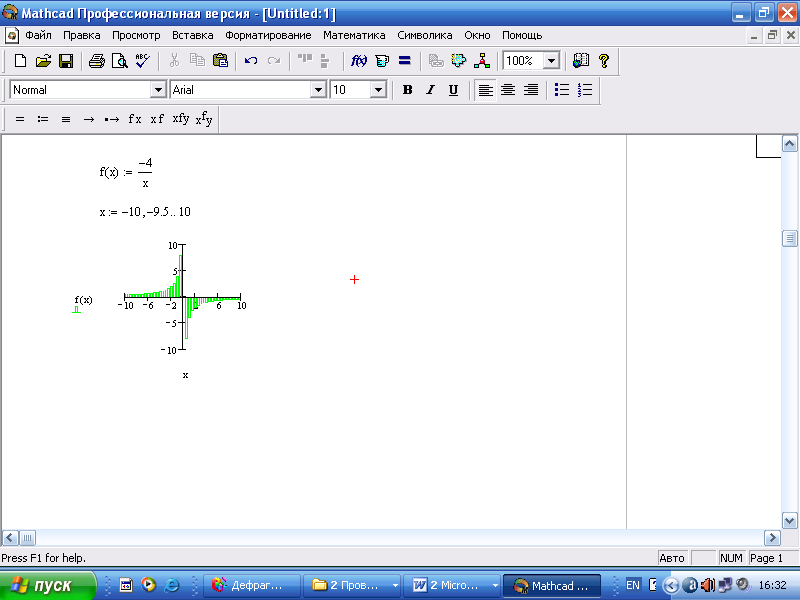
Рис. Вид графика функции после форматирования

4. Чтобы добавить новый график к существующему:

− установите курсор на рабочем поле в строке справа от функции f(x);

− введите с клавиатуры: g(x):=1/x;

− выделите график;

− щелкните мышью на графике функции. Установите курсор справа от f(x);

− наберите на клавиатуре запятую. Курсор перейдет на следующую строку;

− наберите на клавиатуре g(x). Нажмите клавишу <Enter>;

− линию графика g(x) изобразим по своему усмотрению, используя диалоговое окно Formatting Currently Selected X-Y Plot (например, точечный график Type − points, Weight − 2, красного цвета – red, как показано на рис.)

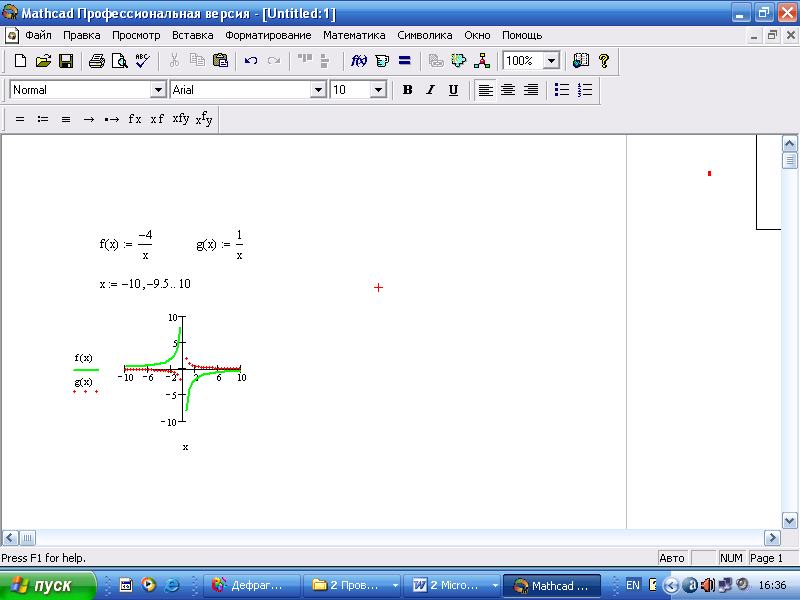
Рис. Полученные графики функций

Варианты индивидуальных заданий

На одной координатной плоскости построить графики функций и , при изменении х от -15 до +15 с шагом 0.1.

№В	f(x)	g(x)	№В	f(x)	g(x)
1			16
2			17
3			18
4			19
5			20
6			21
7			22
8			23
9			24
10			25
11			26
12			27
13			28
14			29
15			30

Задание 5:

Построить график функции z=cos(0,2xy) и получить таблицу ее значений для заданных аргументов.

Методика выполнения задания:

Графически отобразить функцию двух аргументов можно с помощью графика поверхности (Surface Plot), который можно построить несколькими способами:

1. Упрощенный метод построения поверхности аналогичен построению двумерного графика (см. рис.()), а именно:

   1. задается функция двух переменных, например f(x,y):=cos(0.2xy);

   2. определяется место вставки графика и на панели инструментов Построение графика выбирается кнопка ;

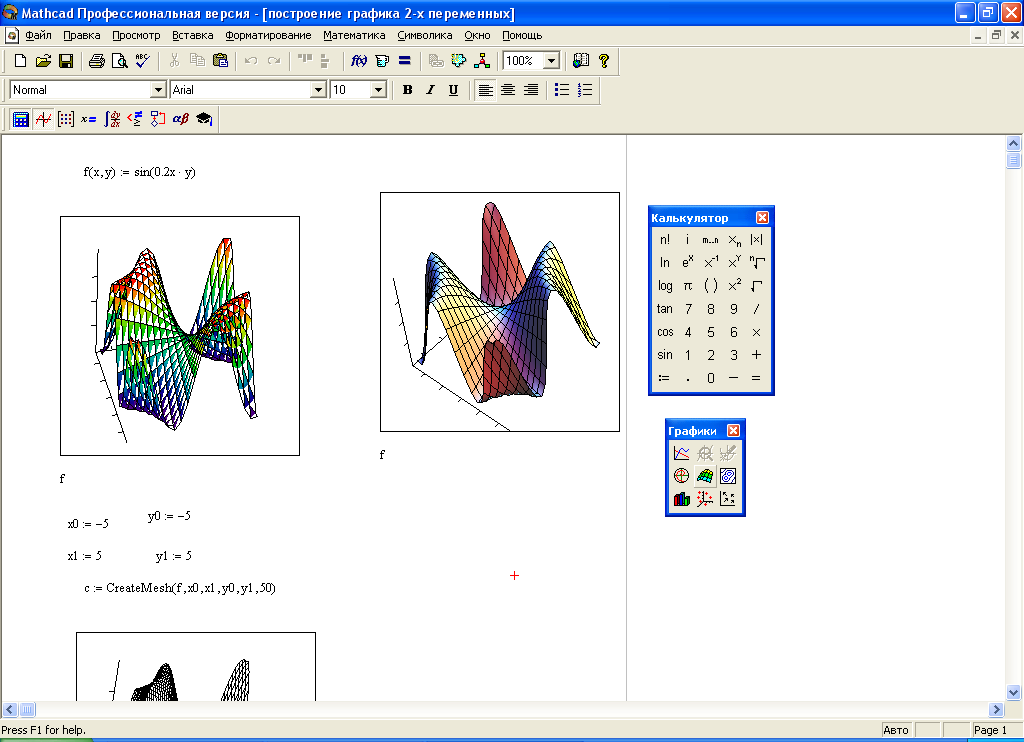   3. в нижнем левом углу задается имя функции, в данном случае f.

Недостатком этого метода построения поверхности является неопределенность в масштабировании, поэтому для получения приемлемого вида графика требуется форматирование.

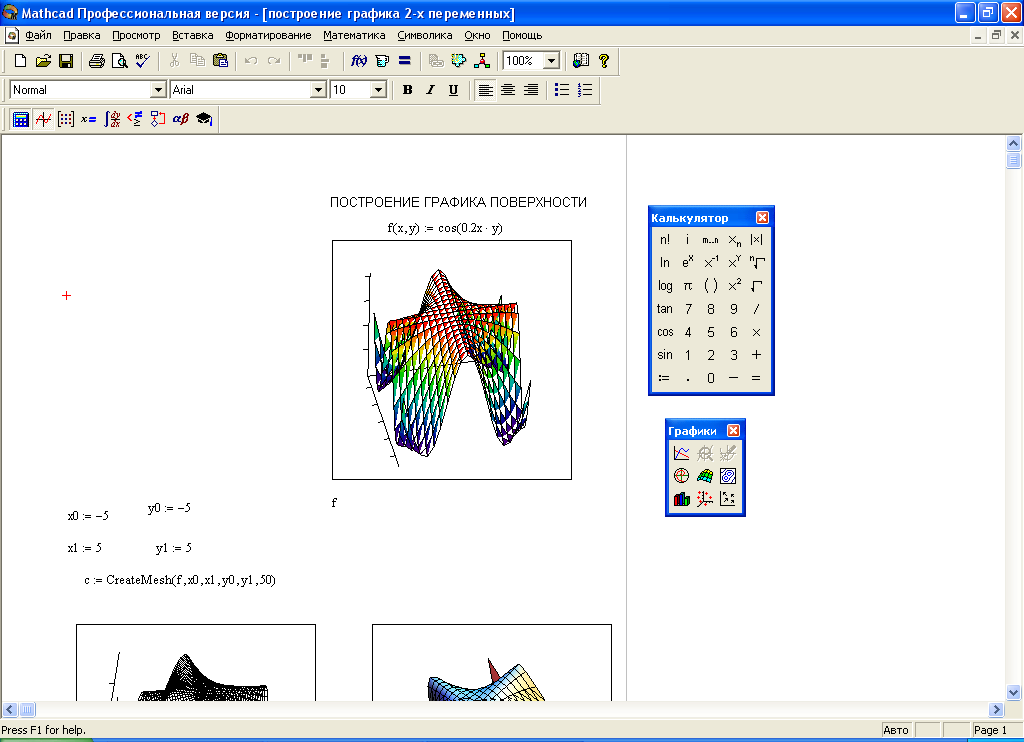
Рис. Построение графика поверхности упрощенным способом

2. Применение мастера построения трехмерных графиков. При использовании такого способа построения графика функции двух переменных необходимо, как и в предыдущих способах, сначала задать функцию и выбрать место вставки графика, затем в пункте меню Вставка выбрать команду График – Мастер 3-d участка и в диалоговом режиме установить необходимые параметры.

3. Применение встроенной функции GreateMesh(F, s0, s1, t0, t1, sgrid, tgrid, fmap). Эта функция возвращает массив из трех матриц, представляющих координаты x, y, z для функции F, определенной в векторной параметрической форме в качестве функции двух переменных sgrid и tgrid. Аргумент fmap – трехэлементный вектор значений, задающих число линий в сетке изображаемой функции. Построение графика функции с помощью данной функции проиллюстрировано на рис.()

Очень часто, особенно при поиске оптимумов функции двух переменных, полезнее просмотреть не график поверхности, а карту линии уровня, которые подобны линиям на физической географической карте, охватывающим горы и впадины (минимумы и максимумы).

На место линий графика можно поставить маленькие стрелочки, отмечающие направление изменения функций двух переменных. Тогда получится векторное поле (Vector Field Plot).

Гибридом декартова графика и графика поверхности является так называемый трёхмерный точечный график (3D Scatter Plot). Его главное отличие от графиков, отображающих прямоугольные матрицы, в том, что с его помощью можно изобразить взаимосвязь трёх векторов.

Графики можно расцветить так, чтобы более высокие зоны имели тёплые цвета, а более низкие – холодные. Пакет MathCAD может раскрасить объёмные конструкции так, чтобы пользователь смог увидеть всё, что ему нужно.

Основной недостаток трёхмерной графики MathCAD и других подобных пакетов – в том, что область изменения аргументов должна быть прямоугольной.

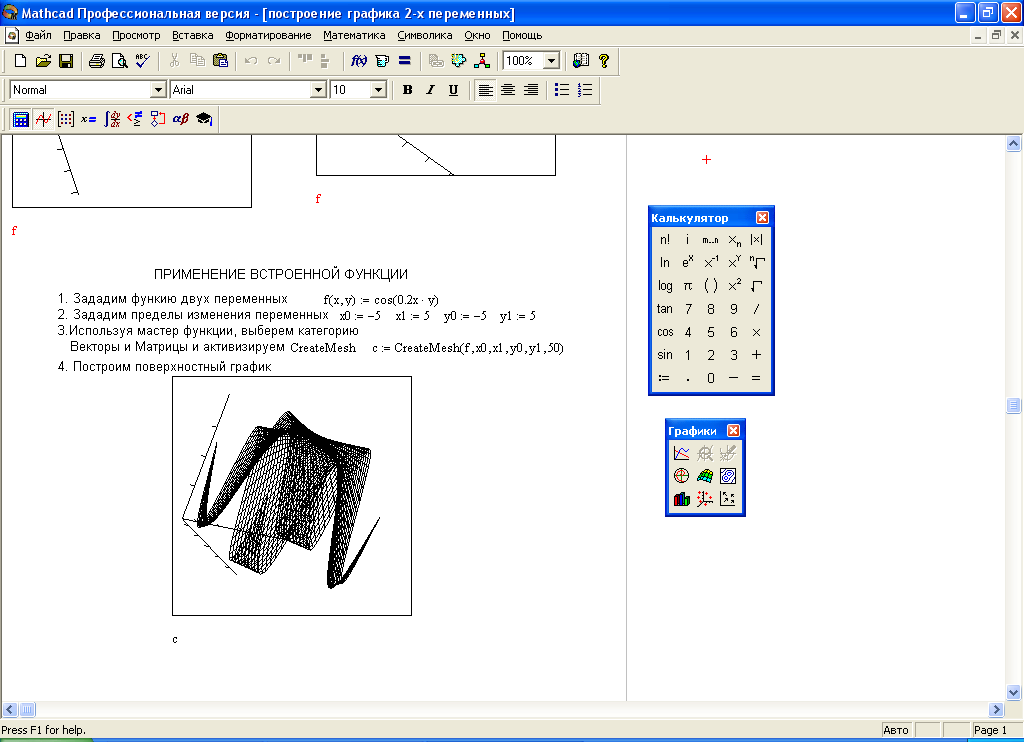
Рис. Построение графика поверхности с помощью встроенной функции

Для выполнения второй части задания необходимо воспользоваться понятием ранжированной переменной.

Варианты индивидуальных заданий

Построить график функции z=f(x,y), где a, b - некоторые константы (задать самостоятельно).

№В	z=f(x,y)	№В	z=f(x,y)
1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.

Задание6: Решить уравнение .

Методика выполнения задания:

Для решения алгебраических уравнений, например квадратных и кубических, а также для вычисления корней полинома очень удобно использовать возможности символьного процессора. Символьными называют такие вычисления, результаты которых представляются в аналитическом виде, то есть в виде формулы. В данном случае речь идет о команде Solve (решить), которая входит в Математическую палитру интегрированной системы MathCad.

Рассмотрим решение уравнения, предложенного в задании с помощью функции Solve:

1. Зададим функцию уже известным нам способом;

2. Определим место вывода результатов решения данного уравнения и выберем команду Solve на панели инструментов Символика, входящей в состав Математической палитры программы MathCad. В появившемся шаблоне функции зададим имя функции, и имя переменной относительно которой ведется решение алгебраического уравнения. Результаты отображены на рис ().

Рис. Решение алгебраического уравнения с помощью функции solve

Варианты индивидуальных заданий

Решить уравнение f(x)=0.

№В	f(x)=0	№В	f(x)=0
1.		16.
2.		17.
3.		18.
4.		19.
5.		20.
6.		21.
7.		22.
8.		23.
9.		24.
10.		25.
11.		26.
12.		27.
13.		28.
14.		29.
15.		30.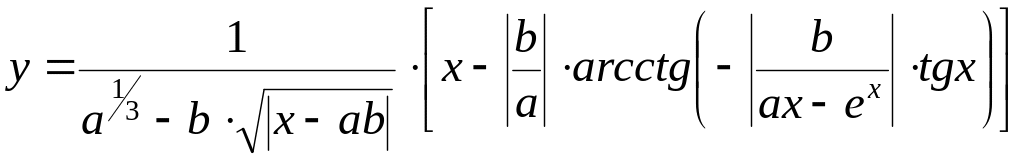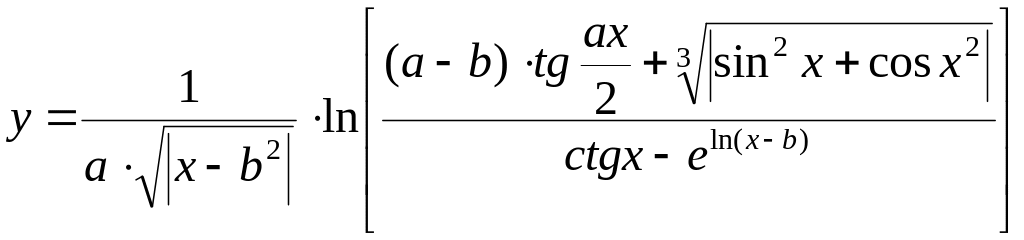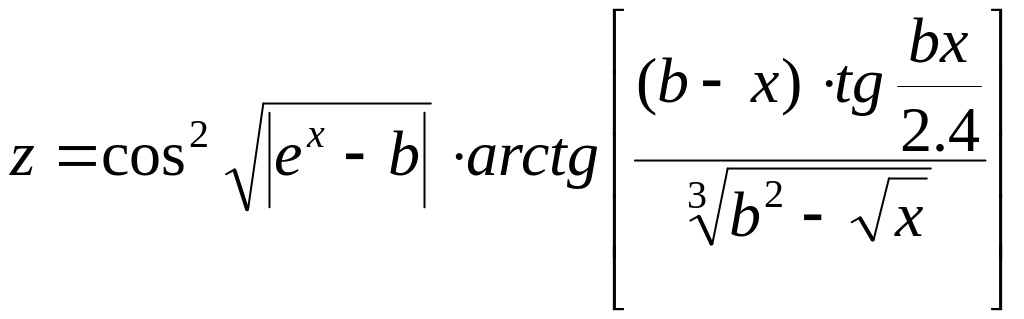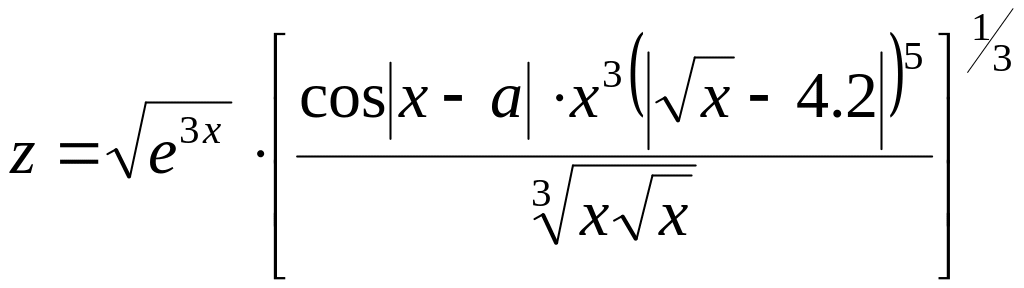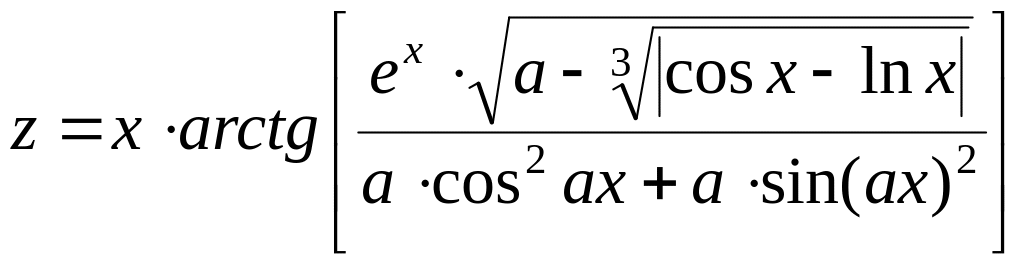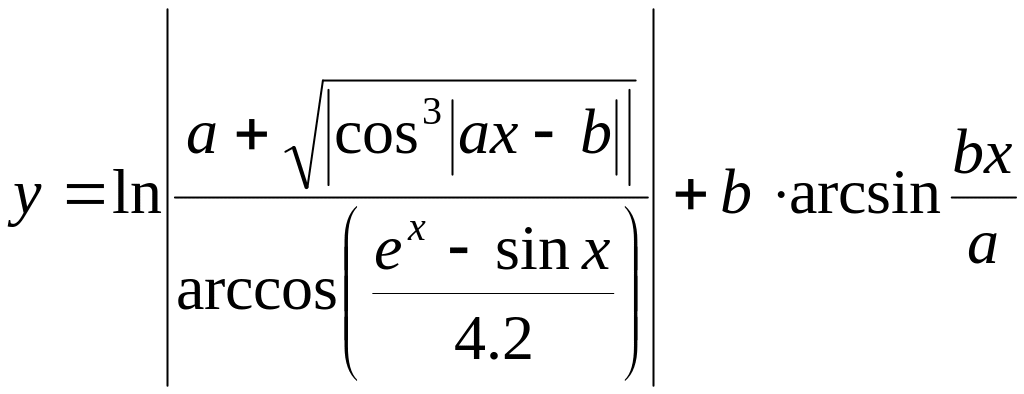