9.3. Работа силы тяжести и силы упругости

Работа силы тяжести. Работа силы тяжести равна взятому со знаком плюс или минус произведению силы тяжести на вертикальное перемещение точки ее приложения

,

где Н – перемещение точки приложения силы по вертикали.

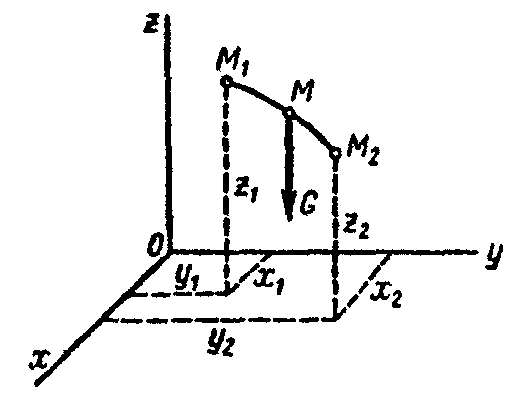
Рис. 3.58

Знак плюс соответствует перемещению точки вниз, а знак минус - перемещению точки вверх (рис. 3.58).

Работа силы тяжести не зависит от вида траектории перемещения точки, а зависит лишь от расстояния, пройденного точкой.

Работа силы упругости. Пружина АВ₁ растягивается только вдоль оси х. Проекция силы упругости P на ось х . Работа силы упругости на перемещении B₁B₂ =h (рис. 3.59)

,

где h – величина деформации пружины.

Наибольшей деформации пружины B₁B₂ соответствует наибольшее значение силы упругости , а потому

.

Рис. 3.59

Если деформация пружины возрастает, работа силы упругости отрицательна. Работа силы упругости положительна, когда деформация уменьшается. Если начальная деформация пружины не равна нулю, а равна х_о, то работа силы упругости на дополнительной деформации ( )

.

9.4. Работа сил, приложенных к твердому телу

а) Поступательное движение. Работа внутренних сил твердого тела при поступательном движении на любом его перемещении равна нулю.

Рис. 3.60

Элементарная работа всех сил, приложенных к телу, равна элемен­тарной работе внешних сил (рис. 3.60):

;

; ,

где - главный вектор всех внешних сил.

Работа на конечном перемещении

.

б) Вращение твердого тела вокруг неподвижной оси. Элементарная работа сил, приложенных к твердому телу, вращаю­щемуся вокруг неподвижной оси, равна произведению главного момента внешних сил относительно оси вращения на приращение угла поворота (рис. 3.61):

.

Рис. 3.61

Если при вращении тела значение его угла поворота изменяется от φ₁ до φ₂, то сумма работ сил на этом конечном перемещении

. (3.35)

В случае, если главный момент внешних сил относительно оси вращения тела постоянен, ,

, (3.27)

т. е. в этом случае сумма работ сил на конечном перемещении равна произведению главного момента внешних сил относительно оси враще­ния на конечное изменение угла поворота тела.

В формуле (3.27) угол поворота выражен в радианах, а размерность работы совпадает с размерностью момента. Пользуясь формулой (3.26), можно определить мощность сил, при­ложенных к твердому телу, вращающемуся вокруг неподвижной оси с угловой скоростью ω:

.

Задача 3.16. Груз 1 массой т₁ = 2 кг приводит в дви­жение каток 2 массой m₂ = 1 кг. Коэффициент трения качения = 0,01 м. Определить ра­боту внешних сил системы при опускании груза 1 на высоту h = 1 м, если радиус катка R = 0,1 м (рис. 3.62).

Рис. 3.62

Решение. Обозначим работу, совершаемую грузом при перемещении, через , а работу катка через .

.

Глава 10. Теоремы об изменении кинетической энергии