Задача 4. Применение общего уравнения динамики к изучению механической системы

Для заданной механической системы определить ускорение груза 1 и натяжение в ветви нити 1, к которой прикреплен груз. Массами нитей пренебречь. Система движется из состояния покоя. Считать, что , , , , см, , f= 0,1 (рис. 1).

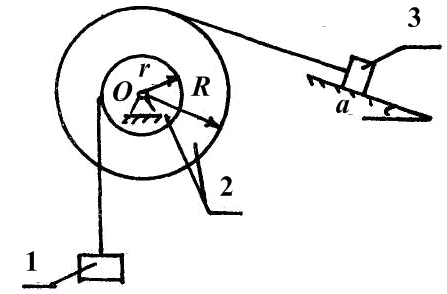
Рис 1

Решение.

1. Составление расчетной схемы. На механическую систему действуют активные силы , , . Применяя принцип освобождаемости от связей к внешним связям, покажем , , N. Силу трения изобразим в сторону, противоположную предполагаемую направлению движения.

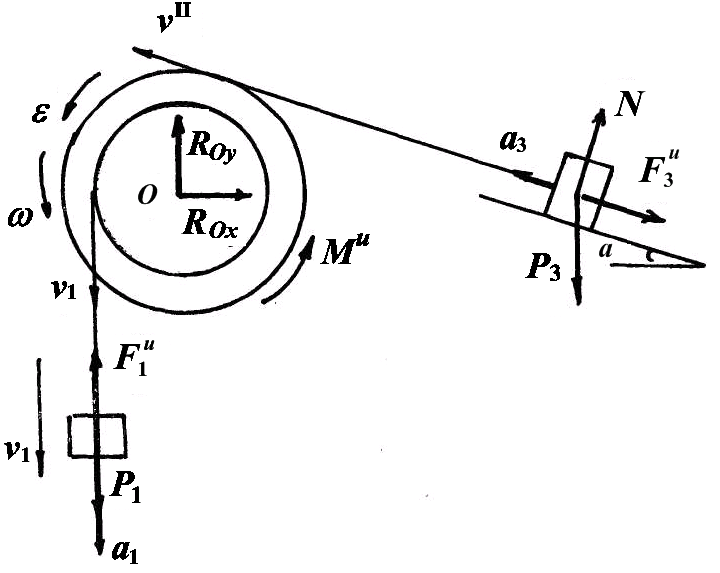
Рис. 2

Так как система пришла в движение из состояния покоя, то ускорения точек системы 1 направлены в сторону движения.

Приложим силы инерции. Тела 1 и 3 движутся поступательно, силы инерции этих тел выражаются векторами

и показываются на расчетной схеме противоположно ускорениям.

Силы инерции блока 2, вращающегося вокруг неподвижной оси Oz с угловым ускорением , приводятся к паре, момент которой равен

и изображается на схеме в сторону противоположную .

2. Выбор теоремы.

Применим общее уравнение динамики

.

Произведение силы, перемещения точки приложения силы и косинуса угла, который образуют сила и направление движения, представляет собой работу силы на данном перемещении.

Работа силы на заданном перемещении равна нулю, если точка приложения силы неподвижна или сила перпендикулярна направлению движения.

3. Составление уравнения.

, (1)

где - возможное перемещение тела 1, - угол поворота блока 2, -возможное перемещение центра масс тела 3 по направлению скорости, -высота, на которую поднимется центр масс тела 3 при перемещении на .

Уравнения связей. В общее уравнение динамики входят неизвестные перемещения. Выразим скорости центров масс и угловую скорость тел системы через скорость тела 1. Зависимости между возможными перемещениями такие же, как и между соответствующими скоростями.

Скорость любой точки обода блока малого радиуса равна скорости тела 1, а также произведению угловой скорости тела 2 и радиуса вращения .

,

отсюда

. (2)

Вращательная скорость любой точки обода блока большого радиуса с одной стороны, равна произведению угловой скорости блока и радиуса вращения R, а с другой - скорости тела 3.

.

Подставляя значение угловой скорости, получим

. (3)

Проинтегрируем при нулевых начальных условиях равенство (2) и (3) и получим соотношения возможных перемещений точек системы

.

Подставим полученные возможные перемещения в (1) и произведем замену

.

Поделив обе части равенства на запишем

Модули силы инерции: тела 1 ; тела 2 .

Момент пары сил инерции

.

Связь между ускорениями точек системы получим, продифференцировав по времени уравнения (2) и (3)

.

Тогда силы инерции точек системы запишутся

; .

Момент инерции блока

.

Тогда

.

Сила трения скольжения

.

В выражение (4) подставим значения сил инерции, силы трения и учитывая, что , запишем

.

4. Определение неизвестных.

.

Откуда

.

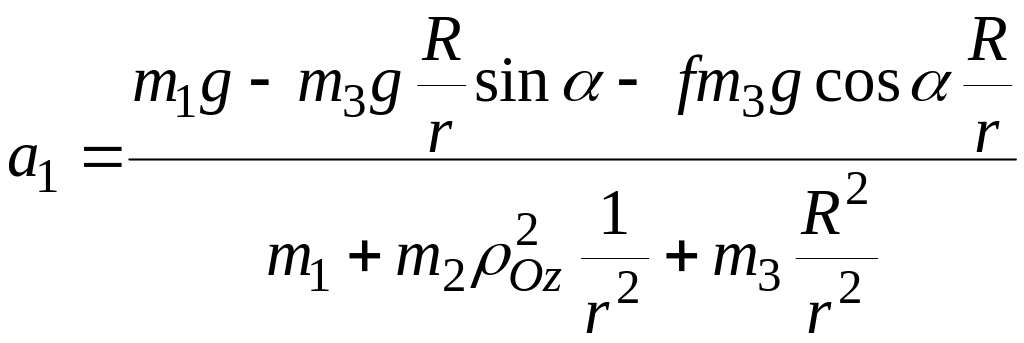Окончательно

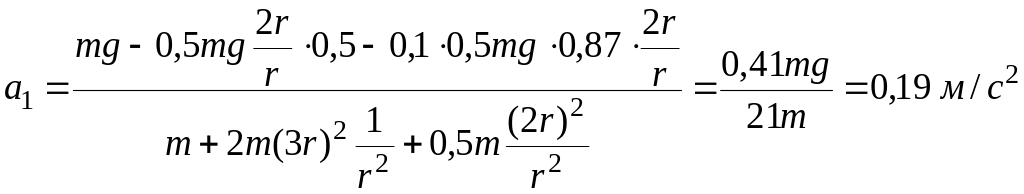
Для определения натяжения в ветви 1 - 2 мысленно разрежем нить и заменим ее действие на груз 1 реакцией .

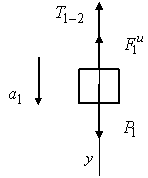
Общее уравнение динамики

.

Откуда

.