11.4. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси

Динамические давления в опорах и их реакции при вращении твердого тела (рис. 3.73,а) вокруг неподвижной оси определяются по формулам:

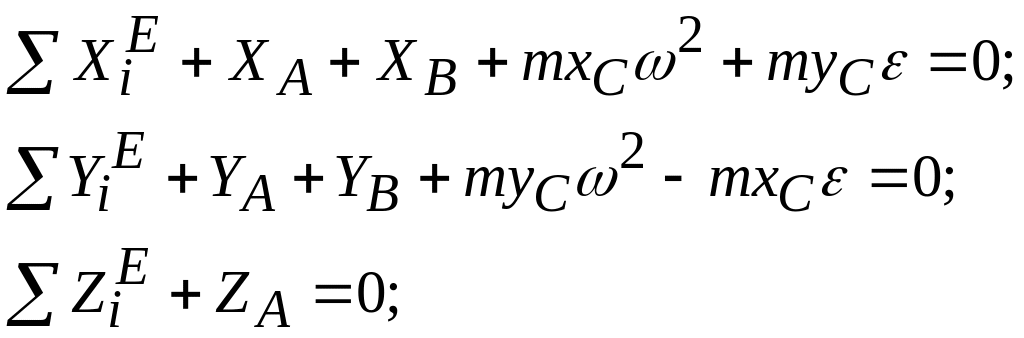
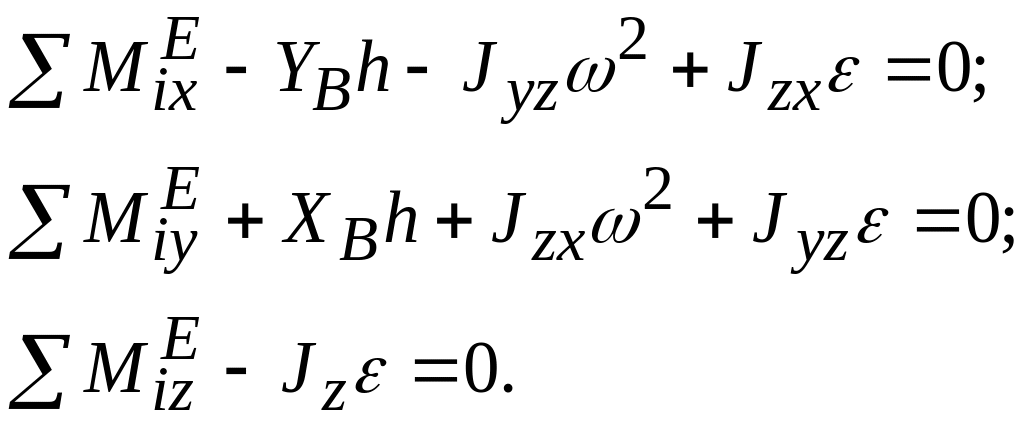
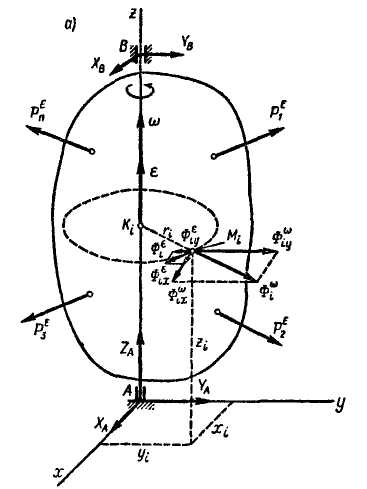
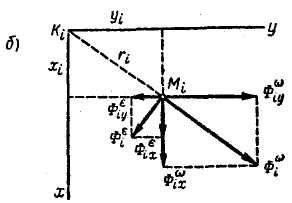
Рис. 3.73

Последнее из уравнений не содержит реакций опор. Это уравнение представляет собой дифференциальное уравнение вращения тела. Остальные пять уравнений позволяют определить пять составляющих реакций подпятника А и подшипника В. В первое, второе, четвертое и пятое уравнения, из которых определяются составляющие реакций опор вдоль осей х и у, входят члены, зависящие как от внешних задаваемых сил, так и от сил инер­ции. Следовательно, каждая из этих реакций имеет статическую состав­ляющую, вызываемую действием внешних задаваемых сил и дина­мическую составляющую, зависящую от сил инерции.

Установлено, что динамические составляющие реак­ций подпятника и подшипника равны нулю в том случае, если ось вращения тела является главной центральной осью инерции тела.

Задача 3.20. Груз массой =100 кг поднимается при помощи лебедки массой =110 кг с постоянным ускорением м/с. Лебедка установлена на горизонтальной балке длиной l = 2,6 м, жестко закрепленной одним концом в стене (рис. 3.74,а). Подъем груза вызывается парой внешних сил, действующих на барабан лебедки, с моментом М=160 Н∙м, радиус инерции барабана равен м, а геометрический радиус R=0,12 м. Определить реакции внешних связей балки.

Решение. Составление расчетной схемы. Объектом изучения является механическая система, состоящая из трех тел: балки, лебедки и груза. Активные силы: - вес груза, - вес лебедки, пара сил с моментом . Система имеет внешние (жесткая заделка) и внутренние (опирание лебедки на балку, трос, связывающий груз и барабан лебедки) связи.

Принцип освобождаемости от связей применяем только к внешней связи, мысленно ее отбрасывая и заменяя действие связи на систему реакциями.

а) б)

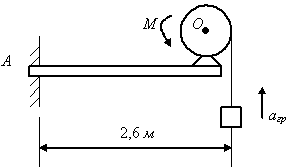
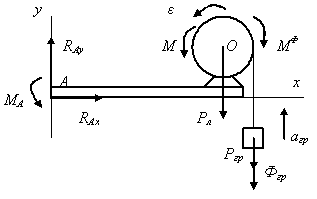
Рис. 3.74

Ускорение груза направлено вертикально вверх. Так как груз движется поступательно и прямолинейно, то полное ускорение груза равно его касательной составляющей

.

Барабан лебедки при заданном направлении ускорения груза имеет угловое ускорение, направленное против часовой стрелки.

Силы инерции точек барабана лебедки приводятся к главному моменту сил инерции , который на расчетной схеме покажем в сторону, противоположную угловому ускорению, а сила инерции груза - в сторону, противоположную ускорению груза.

Систему отсчета изобразим так, чтобы начало отсчета совпало с точкой закрепления балки, направив ось х вдоль оси балки вправо, а ось у – вертикально вверх.

Выбор теоремы. К механической системе приложена плоская произвольная система сил, которую можно привести к главному вектору и

главному моменту , выбрав за центр приведения точку А.

Главный вектор представляет собой геометрическую сумму задаваемых сил, реакций связей и сил инерции, а главный момент - алгебраическую сумму моментов задаваемых сил, реакций связей и сил инерции относительно центра приведения.

Принцип Даламбера запишем, используя главный вектор и главный момент сил, так как в задаче в качестве неизвестных выступают и силы реакции и реактивный момент.

, (а)

. (б)

Составление уравнений. Спроецируем равенство (а) на оси декартовых координат и запишем алгебраическую сумму моментов всех сил, действующих на механическую систему:

(в)

(г)

. (д)

Определение неизвестных параметров. Из уравнения (в) следует, что

.

Из уравнения (г) получим

. (е)

Из уравнения (д) получим

. (ж)

Определение силы инерции груза и момента инерции барабана лебедки:

,

где - момент инерции барабана лебедки относительно оси вращения, проходящей через точку О.

Угловое ускорение в задаче не задано. Чтобы его определить, запишем внутренние связи между лебедкой и грузом. Если трос считать идеальной связью (гибким и нерастяжимым), то выполняется равенство

.

Продифференцировав уравнение связи один раз по времени, получим связь ускорения груза и углового ускорения барабана лебедки

,

откуда

.

Подставим значения , а также заменив вес каждого тела на произведение массы и ускорения свободного падения, запишем:

.

В полученных выражениях часть слагаемых (выделенные рамкой) имеют сомножитель , поэтому при равномерном прямолинейном движении груза или его покое эти слагаемые будут равны нулю.

Части равенств, имеющих сомножителем ускорение, представляют собой динамические соотношения составляющих реакций:

;

.

Остальные слагаемые относятся к статическим составляющим реакций

;

.

Подставляя числовые параметры, определим:

;

;

;

.

Реакции жесткой заделки запишем в виде суммы статических и динамических составляющих:

;

.

Анализ полученных результатов. При ускорении груза , направленным вверх, реакции жесткой заделки увеличиваются за счет динамических составляющих.