
- •5.2. Количество движения материальной точки и механической системы
- •5.3. Теорема об изменении количества движения материальной точки
- •5.4. Теорема об изменении количества движения механической системы
- •Глава 6. Теоремы об изменении момента
- •6.2. Теорема об изменении момента количества движения материальной точки относительно центра и оси
- •6.3. Кинетический момент механической системы относительно центра и оси
- •6.4. Теорема об изменении кинетического момента механической системы относительно центра и оси
- •Глава 7. Динамика твердого тела
- •7.1. Поступательное движение твердого тела
- •7.2. Вращение твердого тела вокруг неподвижной оси
- •7.3. Плоское движение твердого тела
- •Формулу (г) можно представить в виде
- •Глава 8. Динамика сферического и свободного движений твердого тела
- •8.1. Кинетические моменты твердого тела относительно
- •Неподвижной точки и координатных осей
- •8.2. Дифференциальные уравнения сферического движения твердого тела
- •В этом случае уравнения (3.21) принимают вид:
- •8.3. Дифференциальные уравнения движения свободного твердого тела
- •8.4. Элементарная теория гироскопа
- •Глава 9. Работа сил
- •9.1. Работа постоянной по модулю и направлению силы
- •9.2. Элементарная работа силы и методы ее определения
- •9.3. Работа силы тяжести и силы упругости
- •9.4. Работа сил, приложенных к твердому телу
- •Работа на конечном перемещении
- •Глава 10. Теоремы об изменении кинетической энергии
- •10.1. Кинетическая энергия твердого тела при различных
- •Движениях
- •10.2. Теорема об изменении кинетической энергии материальной точки
- •10.3. Кинетическая энергия механической системы
- •10.4. Теорема об изменении кинетической энергии механической системы
- •10.5. Потенциальное силовое поле и потенциальная энергия
- •Глава 11. Принцип Даламбера для материальной точки и механической системы
- •11.1. Принцип Даламбера для материальной точки
- •11.2. Принцип Даламбера для механической системы
- •11.3. Приведение сил инерции точек твердого тела к простейшему виду
- •11.4. Определение динамических реакций подшипников при вращении твердого тела вокруг неподвижной оси
- •Глава 12. Принцип возможных перемещений
- •12.1. Принцип возможных перемещений
- •12.2. Общее уравнение динамики
- •Задача 4. Применение общего уравнения динамики к изучению механической системы
- •Глава 13. Дифференциальное уравнение движения механической системы в обобщенных координатах
- •13.1. Обобщенная сила
- •13.2. Уравнения Лагранжа второго рода
 .
.
Проекции импульса силы на оси координат:

Здесь
![]() проекции переменной силы
проекции переменной силы
![]() на оси координат. Модуль и направление
импульса силы определяются по его
проекциям:
на оси координат. Модуль и направление
импульса силы определяются по его
проекциям:
![]() ;
;
![]() .
.
5.2. Количество движения материальной точки и механической системы
Количество движения материальной точки – векторная мера ее движения, равная произведению массы точки на ее вектор скорости:
![]() .
.
Количество движения механической системы или главный вектор количества движения – геометрическая сумма количеств движений всех материальных точек системы
![]() .
.
Главный вектор количества движения системы можно определить по формуле
![]() ,
,
где
![]() -
скорость центра масс системы.
-
скорость центра масс системы.
Модуль главного вектора количества движения системы определяется через его проекции на оси декартовых координат:
![]() ,
,
где
![]() -
проекции количества движения i-
го тела
системы на
оси декартовых координат. Тогда
-
проекции количества движения i-
го тела
системы на
оси декартовых координат. Тогда
![]() .
.
5.3. Теорема об изменении количества движения материальной точки
а) Дифференциальная форма: производная по времени от количества движения материальной точки геометрически равна равнодействующей сил, приложенных к этой точке.
![]() .
.
б) Интегральная (конечная) форма: изменение количества движения материальной точки за некоторый промежуток времени равно геометрической сумме импульсов cил, приложенных к точке за тот же промежуток времени. Эту теорему называют также теоремой импульсов,
![]() .
.
Векторному уравнению соответствуют три уравнения в проекциях на оси координат:

Уравнения показывают, что изменение проекции количества движения
материальной точки на данную ось за некоторый промежуток времени равно сумме проекций на ту же ось импульсов приложенных к точке сил за тот же промежуток времени.
Задача 3.10. Груз спускается вниз по шероховатой наклонной поверхности, расположенной под углом a к горизонту; f - коэффициент трения скольжения груза о наклонную плоскость. В начальный момент времени скорость груза равнялась v. Через какой промежуток времени скорость груза удвоится (рис. 3.35)?

Рис. 3.35
Решение.
Изобразим силы, приложенные к грузу:
![]() - вес груза,
- вес груза,
![]() - нормальная сила реакции плоскости,
- нормальная сила реакции плоскости,
![]() - сила трения скольжения груза о
плоскость, причем
- сила трения скольжения груза о
плоскость, причем
![]() .
.
Направляем ось х вдоль наклонной плоскости вниз. Запишем теорему об изменении количества движения материальной точки в проекции на ось х:
![]() .
.
Согласно
условию задачи,
![]() ,
,
![]() .
Так как все силы, приложенные к грузу,
постоянны, то
.
Так как все силы, приложенные к грузу,
постоянны, то
![]() ,
,
где τ - искомый промежуток времени. Следовательно,
![]() ,
,
откуда
![]()
5.4. Теорема об изменении количества движения механической системы
a) Дифференциальная форма: производная по времени от количества движения механической системы геометрически равна главному вектору внешних cuл, действующих на эту систему.
![]() .
.
Векторному уравнению соответствуют три уравнения в проекциях на оси координат: производная по времени от проекции количества движения механической системы на любую ось равна проекции главного вектора внешних cuл, действующих на систему, на ту же ось.
![]() .
.
б) Интегральная форма: изменение количества движения механической системы за некоторый промежуток времени равно геометрической сумме импульсов внешних сил, приложенных к системе, за тот же промежуток времени.
![]() .
.
Векторному уравнению соответствуют три уравнения в проекциях на оси координат: изменение проекции количества движения механической системы на любую ось равно сумме проекций импульсов всех внешних сил, действующих на систему, на ту же ось
![]()
С л е д с т в и е 1. Если векторная сумма всех внешних сил, приложенных к системе, равна нулю, то вектор количества движения системы не изменяется ни по модулю, ни по направлению.
С л е д с т в и е 2. Если сумма проекций всех внешних сил, приложенных к системе, на какую-нибудь ось равна нулю, то проекция вектора количества движения системы на ту же ось есть величина постоянная.
Следствия 1 и 2 называют законом сохранения количества движения системы, который формулируется так: внутренние силы не могут изменить
количество движения механической системы.
Задача
3.11. Материальная
система состоит из груза А
весом
![]() ,
лежащего на наклонной плоскости клина
В
весом
,
лежащего на наклонной плоскости клина
В
весом
![]() ,
расположенной под углом
,
расположенной под углом
![]() к горизонту. В начальный момент система
находилась в покое; затем груз А
начал скользить по наклонной плоскости
с относительной скоростью
к горизонту. В начальный момент система
находилась в покое; затем груз А
начал скользить по наклонной плоскости
с относительной скоростью
![]() .
Определить скорость движения клина В.
Силой трения скольжения клина о
горизонтальную плоскость пренебречь
(рис. 3.36, а).
.
Определить скорость движения клина В.
Силой трения скольжения клина о
горизонтальную плоскость пренебречь
(рис. 3.36, а).
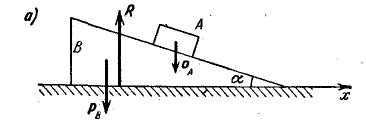

Рис. 3.36
Решение. В состав рассматриваемой материальной системы входят два тела: груз А и клин В. Изобразим все внешние силы системы: — вес груза, — вес клина, — нормальная сила реакции горизонтальной плоскости (было бы ошибочным изображение нормальной силы реакции наклонной плоскости, приложенной к грузу, так как эта сила по отношению к системе, состоящей из груза и клина, является внутренней).
Направим ось х по горизонтали направо.
Запишем теорему об изменении главного вектора количеств движения системы материальных точек в проекции на ось х:
![]() .
.
Так
как сумма проекций всех внешних сил
на ось х
равна нулю:
![]() ,
то и сумма проекций импульсов всех
внешних сил на эту ось тоже равна нулю:
,
то и сумма проекций импульсов всех
внешних сил на эту ось тоже равна нулю:
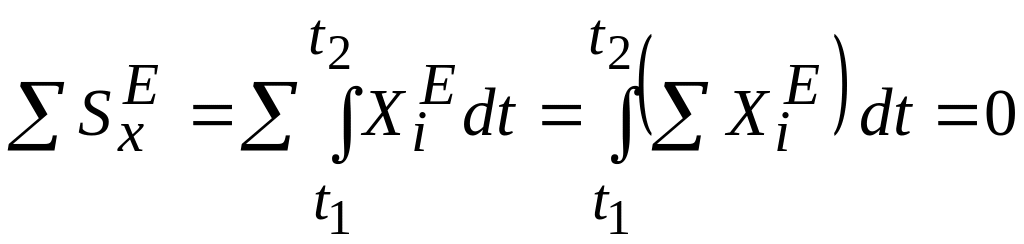 .
.
Тогда
![]() ,
,
т.
е.
![]() .
.
Следовательно, имеет место случай сохранения проекции на ось х главного вектора количеств движения системы.
В
начальный момент система находилась
в покое, т. е.
![]() .
.
Вычислим
проекцию на ось х
главного вектора количеств движения
системы в рассматриваемый момент
времени. Допустим, что клин В
движется направо с искомой скоростью
![]() .
Для нахождения скорости груза А
надо применить теорему о сложении
скоростей точки
.
Для нахождения скорости груза А
надо применить теорему о сложении
скоростей точки
![]() .
Груз А
совершает переносное поступательное
движение вместе с клином В,
т. е.
.
Груз А
совершает переносное поступательное
движение вместе с клином В,
т. е.
![]() ,
и относительное движение по отношению
к клину В,
т. е.
,
и относительное движение по отношению
к клину В,
т. е.
![]() .
.
Следовательно,
![]() .
( рис. 3.36, б)
и
.
( рис. 3.36, б)
и
![]() .
.
Теперь можно вычислить проекцию главного вектора количеств движения системы на ось х:
![]() .
.
Как было показано, , т. е.
![]() ,
,
откуда
![]() .
.
Знак
минус указывает, что в действительности
клин В
движется налево, т. е. вектор
![]() направлен в противоположную сторону.
направлен в противоположную сторону.
Задача 3.12. Колесо весом G и радиусом R (рис. 3.37) катится без скольжения по рельсу, делая n об/мин. Определить количество движения колеса.

Рис. 3.37
Решение. Количество движения колеса
![]() .
.
Скорость vC центра масс колеса определяется как вращательная скорость вокруг мгновенного центра скоростей, находящегося в точке Р соприкасания колеса с рельсом:
![]() .
.
Так как
![]() ,
то
,
то
![]() .
.
Подставляем значения m и vC в выражение, определяющее К,
![]() .
.
